【论文快读】人群计数FIDTM

Focal Inverse Distance Transform Maps for Crowd Localization and Counting in Dense Crowd

• 华中科大，北邮
• 挺实用，推理有些慢(同事使用感受)

最近接触了一个人群密度估计的工作，就看了这篇去年的论文。标题中的Focal Inverse Distance Transform Maps（FIDT map）就点出了他们的主要贡献，for Crowd Localization and Counting in Dense Crowd表示目的是要做人群的定位和密集人群计数。下图是总的pipeline。

一般来说，基于CNN的人群密度估计的方法有三种：基于检测的，基于回归的，Density map的。Density map预测每个像素存在人头点的概率分布，他的标注一般是在人头除点一个点，这种方法计数精度高，位置精度中等，缺点是低密度场景计数精度差（相对另外两类方法而言）。基于归回的方法是直接预测人数，计数精度中等，标记简单，缺点是缺少位置信息，缺乏可解释性。

后来Inverse Distance Transform被用在人群计数领域，相当于把回归和density map的的方法结合了。先看Distance Transform，它是把map上每个像素用到最近标记点的距离来表示

$$P(x,y)=\underset{(x^{\prime },y^{\prime })\in B}{\min }\sqrt{(x-x^{\prime }{)}^2+(y-y^{\prime }{)}^2}$$

P(x,y)表示map上任意一点(x,y)上的值，B是标记点的集合。Inverse Distance Transform (IDT) 就是取倒数, C是常量1，避免除0，也保证值域为[0,1]（P(x,y)取0时I’=1，P(x,y)取+∞时I’趋向于0 ）

$$I^{\prime }=\frac{1}{P(x,y)+C}$$

这种方法是预测每个像素的IDT，而IDT值高的点(P(x,y)接近0)就是人头所在位置, 这种点称作local maxima, 相当于候选人头中心点，再通过一些过滤策略后得到接近真实的人头中心点，再数这些点的数量获得人数。这篇文章认为IDT在前景(人头区域内)下降太快，在背景处下降太慢，这使得背景不容易和前景区分。提出了FIDT, 相当于加了调节器，通过α和β来控制表达式随P(x,y)增大的下降趋势。文中有消融实验说明α=0.02, β=0.75是比较好的选择

$$I^{\prime }=\frac{1}{P(x,y{)}^{(\alpha \times P(x,y)+\beta )}+C}$$

下图FIDT map的背景部分颜色更深，能更清楚地看到前景区域（亮点外一圈浅蓝色区域）和背景区域的区别。

该文以HRNET为主干网络，加一个卷积和两个反卷积作为head, 回归head上每个点的FIDT值。怎么得到人数？该文提出了Local Maxima Detection Strategy(LMDS) ， 人头点检测策略。

这样就得到人数和人头中心坐标了。

他们的另一项重要工作是I-SSIM loss。仅用预测的特征图和FIDT map的MSE损失，他们觉得不足以约束人头区域的学习。前人已经用了SSIM loss

$$SSIM(E,G)=\frac{(2{\mu }_E{\mu }_G+{\lambda }_1)(2{\sigma }_{EG}+{\lambda }_2)}{({\mu }_E^2+{\mu }_G^2+{\lambda }_1)({\sigma }_E^2+{\sigma }_G^2+{\lambda }_2)}$$

$$L_S=1-SSIM(E,G)$$

E表示estimated map, G表示groundtruth map, μ和${\sigma }^2$分别表示map的均值和方差，${\sigma }_{EG}$表示E和G的协方差，λ1=0.0001， λ2=0.0009，避免除0 。SSIM范围是[-1,1], 这个值越大代表两个图越像，这在评价图像质量里常用。那么损失就是加个1减咯。一般用时会用一个滑动窗口去扫描全图，不区分前景背景。他们认为对于定位任务，损失应该关注前景区域，关注local maxima区域，The global SSIM loss may generate high responses, causing some false local maxima in the background. 这个解释我感觉没说清楚，为什么全局SSIM loss产生高响应，高响应为什么导致误检？hmm… 反正他提出了I-SSIM loss，实验效果还不错，用比不用好（T_T） cv里很多论文就是这样的风格，尽管开源的代码里还没有看到实现。

$$L_{I-S}=\frac{1}{N}\sum _{n=1}^N{L}_s(E_n,G_n)$$

这里的I是independent的意思，对每个indenpendent instance region计算SSIM loss再求和。region的大小被设置为30x30. 前面说了关注local maxima，instance可能指的就是local maxima, 即候选头中心点。下图是这两个loss的对比实验结果。

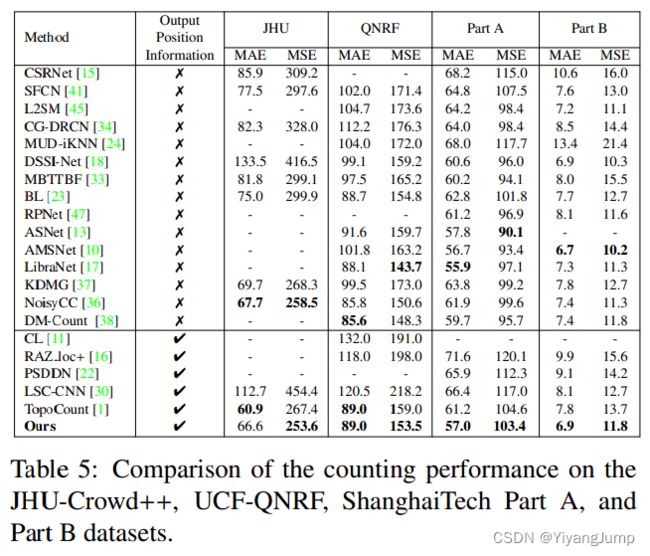
人群密度估计任务中在做定位的评价时，是需要将预测点和标记点做匹配的，匹配上了才算位置对了，匹配需要距离阈值σ，小于阈值说明预测点和标记点匹配上了。上边的实验就取的σ=8。下表是和其他网路的评价对比