无数据蒸馏方向文献_1
初认无数据知识蒸馏
- Large-Scale Generative Data-Free Distillation
-
- Introduction & Related Work
- 具体实现
-
- 知识蒸馏
- 图像生成模型
-
- Inceptionism loss
- Moment matching loss
- 总损失函数
- 实验结果
-
- CIFAR-10
- CIFAR-100
- ImageNet
Large-Scale Generative Data-Free Distillation
这篇文章是老师推荐的,也是看得第一篇无数据知识蒸馏方向的文章。初看这篇文章感觉很牛逼,感觉idea很牛逼,实验结果也很好。但是深入了解,看了其他几篇引文后,感觉含金量并不是特别足。
概括一下摘要:目前存在的知识蒸馏方法往往需要获得原始的训练数据,而一些无数据的知识蒸馏比较耗时,或是无法运用到大数据集上(Imagenet)。这篇文章利用经过训练的教师网络来训练生成网络(generator),并在 C I F A R − 10 CIFAR-10 CIFAR−10和 C I F A R − 100 CIFAR-100 CIFAR−100上取得了 95.02 % 95.02\% 95.02%和 77.02 % 77.02\% 77.02%的准确率。并且能够运用到 I m a g e N e t ImageNet ImageNet数据集上。在这篇文章之前,从来没有生成模型在无数据情况下跑Imagenet。
Introduction & Related Work
尽管有”解释性“方向的工作指出不同层的特征代表不同含义,但神经网络总体上还是个黑箱。知识蒸馏是一种鲁棒性较好的,将大网络”知识“转移到小网络的方法。但知识蒸馏又有自己的问题:
- 知识蒸馏在”蒸馏“环节仍然需要原始数据,而一些特殊的信息因为隐私和安全问题不能直接得到。
- 不能用于某些特定的框架中(如联邦学习,这里不懂)
- 对于无数据知识蒸馏,它往往很费时,而且难以扩展到大数据集。
这篇文章针对上问题,用”生成模型“生成有效数据,并探索了将生成器模型扩展到生成大图片上(imagenet)。设计的总体结构如下图:
的
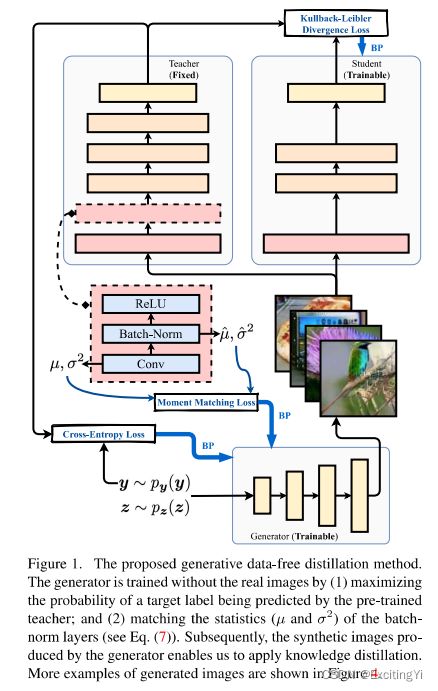
对生成器来说有两个损失函数——交叉熵损失函数和 M o m e n t M a t c h i n g L o s s Moment \ Matching\ Loss Moment Matching Loss,抽象点说,前者是限制头和尾,后者是限制中间部分。让生成的网络不那么离谱。这两个损失函数在下文会详细介绍。
在相近工作中,作者主要介绍了两大方向:1. 生成模型。2. 知识蒸馏。对于生成模型,主流的是GAN网络,但是GAN网络在大规模的数据上表现得不是特别好;另一种方法是最近兴起的可逆网络(reversible networks)(个人理解:前者是训练网络参数,后者是训练输入图像。DeepDream应该就是可逆网络?我看的另外几篇无数据知识蒸馏的文章都是训练”输入数据“的,而非训练生成器的网络参数)。对于知识蒸馏,主要是数据依赖的和无数据的,文章提到之前的无数据知识蒸馏大多都是通过给定一个确定的类别,来训练输入的随机噪声,这就需要哪个噪声经过很多轮迭代才能收敛,很耗时;也有其他文章使用了其他方法,比“训练噪声”的方法效率更高,但无法扩展到大数据集上。
上面都是原文的说法,但其实有点问题:文章说训练网络参数的方法要比训练噪声(也就是输入图像)的方法要更高效。可能是训练n张图像——>需要n*epoch轮反向传播的过程。但如果是训练网络,训练好后只需要一次前馈就可以了。但问题在于如果数据较少,训练网络的过程真的更省时间吗? 另外,文章对CIFAR-100和ImageNet这两个数据集,都用了多个生成器——多少类就多少生成器。虽然生成器的模型比较简单,但这还是有点恐怖的。
具体实现
知识蒸馏
对于一般的知识蒸馏,训练的损失函数公式如下:
L K D = E x ∼ p data ( x ) [ D K L ( T ( x ) ∥ S ( x ) ) ] \mathcal{L}_{\mathrm{KD}}=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}\left[D_{\mathrm{KL}}(T(\boldsymbol{x}) \| S(\boldsymbol{x}))\right] LKD=Ex∼pdata (x)[DKL(T(x)∥S(x))]
知识蒸馏相关知识这篇博客整理的很好,我大概看了一下前面几节理解了个大概,对各种知识蒸馏的改进、变种没有深究。上式中S(x)是学生网络,其中的参数是可训的。这个损失函数训练的结果是让S(x)和T(x)尽量接近。设想T(x)是一个完美的网络,能百分百预测出标签,而且输出是one-hot的张亮,那上面那个KL三度的损失函数就变成了交叉熵损失函数。
但对于生成网络的训练,全过程和知识蒸馏没有一点关系(或者说和学生网络没关系),是先训完生成器,再知识蒸馏训学生网络。
图像生成模型
生成模型(Generator)是对我造成困扰最大的一个模块,看了好多遍看不懂,一方面是没有生成网络的先导知识,另一方面是作者居然一直点名用啥方法生成图像。我也不知道是reversible model还是类GAN生成图像,后来在逼站跟着李沐看了一遍GAN的论文解读,又看了几篇引文,结果在今天上午才突然发现这篇文章的附录里有说生成器的模型是啥…
生成器的模型会放在实验部分介绍,其实和我想象的差距还是很大的,本以为生成器也会像ResNet一样的这种奇形怪状的网络,但发现它的结构意外简单。
文章对生成器如何生成图片的介绍也很复杂,最后还是看GAN网络看懂的。实际上,就是训练一个生成器 G ( z ∣ y ; θ g ) G\left(\boldsymbol{z} \mid \boldsymbol{y} ; \theta_{g}\right) G(z∣y;θg),这里的 z z z是随机生成的输入,本文中对CIFAR10和CIFAR100用1024维的正态分布张量,ImageNet用512维(为啥Imagenet反而更小一点呢?)。 θ g \theta_{g} θg是可训练的权重。 y y y是输入的标签(想要生成的类别)。
下面介绍个人认为全篇文章最重要的几个损失函数。
Inceptionism loss
这是最基础的一个损失函数,在DAFL这篇较早的无数据知识蒸馏的文章就提出了。说是基于Inception的一个损失函数(但是Inception在我的印象里就是一个很胖的结构啊…不知道和这个有啥关系,但不知道也能看懂)
L I n c ( x , y ^ ) = L C E ( x , y ^ ) + L R e g ( x ) \mathcal{L}_{\mathrm{Inc}}(x, \hat{y})=\mathcal{L}_{\mathrm{CE}}(x, \hat{y})+\mathcal{L}_{\mathrm{Reg}}(x) LInc(x,y^)=LCE(x,y^)+LReg(x)
第一项是标准的交叉熵损失函数,其中 y ^ \hat{y} y^是预设的需要产生的类别。后面一项是惩罚项。 L R e g ( x ) = λ t L t ( x ) + λ ℓ 2 L ℓ 2 ( x ) \mathcal{L}_{\mathrm{Reg}}(x)=\lambda_{\mathrm{t}} \mathcal{L}_{\mathrm{t}}(x)+\lambda_{\ell_{2}} \mathcal{L}_{\ell_{2}}(x) LReg(x)=λtLt(x)+λℓ2Lℓ2(x),其中 L t \mathcal{L}_{\mathrm{t}} Lt为总体的方差, L ℓ 2 \mathcal{L}_{\ell_{2}} Lℓ2为 l 2 l_2 l2范数。(搞不懂方差为啥也要惩罚啊…)
我是将他理解为,使产生的图像可以被教师网络“认识”,是属于,固定住教师网络的两头。
Moment matching loss
这个损失函数比较有趣,这篇文章中提到:之前有工作表明,神经网络中的不同层会提取不同类型的特征,如低层倾向于提取边缘棱角,深层会提取更抽象的特征。另一份工作指出,如果只用inceptionism这个方法来生成图像,可能会导致中间激活层的信息消失。这就要求我们需要在神经网络的中间层也加以约束。
在网络中的BN层就保留有该特征图的均值和方差的信息。我们可以利用这一信息,将随机生成图片经过网络后每一层特征图的均值方差都和保存在BN层的均值方差给匹配上。这样就能约束教师网络的中间层。
L M ( x ) = λ S ∑ l [ ∥ μ l ( x ) − μ ^ l ∥ 2 + ∥ σ l 2 ( x ) − σ ^ l 2 ∥ 2 ] \mathcal{L}_{\mathrm{M}}(x)=\lambda_{\mathrm{S}} \sum_{l}\left[\left\|\mu_{l}(x)-\hat{\mu}_{l}\right\|_{2}+\left\|\sigma_{l}^{2}(x)-\hat{\sigma}_{l}^{2}\right\|_{2}\right] LM(x)=λSl∑[∥μl(x)−μ^l∥2+∥∥σl2(x)−σ^l2∥∥2]
这里的损失函数也很简洁。(这个Moment loss还有另外一种交叉熵的形式,本文没用这种,但在另外一篇文献中用到了)
总损失函数
最后总的损失函数就是 L Image ( x , y ) = L Inc ( x , y ) + L M ( x ) \mathcal{L}_{\text {Image }}(x, y)=\mathcal{L}_{\text {Inc }}(x, y)+\mathcal{L}_{\mathrm{M}}(x) LImage (x,y)=LInc (x,y)+LM(x),如果把x换成用生成模型G生成的形式,损失函数如下:
L G = E z ∼ p z ( z ) , y ∼ p y ( y ) [ L Inc ( G ( z ∣ y ) , y ) + L M ( G ( z ∣ y ) ) ] . \mathcal{L}_{\mathrm{G}}=\mathbb{E}_{\boldsymbol{z} \sim p_{z}(\boldsymbol{z}), \boldsymbol{y} \sim p_{y}(\boldsymbol{y})}\left[\mathcal{L}_{\text {Inc }}(G(\boldsymbol{z} \mid \boldsymbol{y}), \boldsymbol{y})+\mathcal{L}_{\mathrm{M}}(G(\boldsymbol{z} \mid \boldsymbol{y}))\right] . LG=Ez∼pz(z),y∼py(y)[LInc (G(z∣y),y)+LM(G(z∣y))].
实验结果
这里主要讲一下最后的实验结果,实验的具体参数不做过多赘述。
CIFAR-10
CIFAR-10生成器的网络结构参数:
z ∈ R 1024 ∼ N ( 0 , I ) OneHot ( y ) ∈ R K Linear ( 1024 + K ) → 8 × 8 × 128 Reshape, BN, LeakyReLU Upsample × 2 3 × 3 Conv 128 → 64 , BN, LeakyReLU 3 × 3 Conv 64 → 3 , Tanh Upsample × 2 Conv 128 → 128 , BN, LeakyReLU \begin{gathered} \hline z \in \mathbb{R}^{1024} \sim \mathcal{N}(0, I) \\ \text { OneHot }(y) \in \mathbb{R}^{K} \\ \hline \text { Linear }(1024+K) \rightarrow 8 \times 8 \times 128 \\ \hline \text { Reshape, BN, LeakyReLU } \\ \hline \text { Upsample } \times 2 \\ \hline 3 \times 3 \text { Conv } 128 \rightarrow 64, \text { BN, LeakyReLU } \\ \hline 3 \times 3 \text { Conv } 64 \rightarrow 3, \text { Tanh } \\ \hline \text { Upsample } \times 2 \\ \hline \text { Conv } 128 \rightarrow 128, \text { BN, LeakyReLU } \\ \hline \end{gathered} z∈R1024∼N(0,I) OneHot (y)∈RK Linear (1024+K)→8×8×128 Reshape, BN, LeakyReLU Upsample ×23×3 Conv 128→64, BN, LeakyReLU 3×3 Conv 64→3, Tanh Upsample ×2 Conv 128→128, BN, LeakyReLU
其中对于CIFAR-10数据集,只用了一个生成器,所以上面的K=1。上面还是有一些没懂的地方,不知道Upsample是啥…后面花个十来分钟补一下就好了。
其中教师网络为ResNet-34,学生网络为ResNet-18最后得到的结果如下:
Model Method Accuracy ResNet-34 Supervised Training 95.05 % † ResNet-18 Supervised Training 93.92 % ‡ ResNet-18 Knowledge Distillation [23] 94.34 % ‡ ResNet-18 Gaussian Noise 11.43 % DAFL [5] 92.22 % DFAD [11] 93.3 % Adaptive DeepInversion [55] 93.26 % ResNet-18 Ours L Inc L M •inceptionism ✓ 77.31 % •moment matching ✓ 94.61 % •both ✓ ✓ 95.02 % \begin{array}{lllr} \hline \text { Model } & \text { Method } & & & \text { Accuracy } \\ \hline \text { ResNet-34 } & \text { Supervised Training } & & & 95.05 \%^{\dagger} \\ \text { ResNet-18 } & \text { Supervised Training } &&& 93.92 \%^{\ddagger} \\ \text { ResNet-18 } & \text { Knowledge Distillation [23] } &&& 94.34 \%^{\ddagger} \\ \hline \text { ResNet-18 } & \text { Gaussian Noise } &&& 11.43 \% \\ & \text { DAFL [5] } & & & 92.22 \% \\ & \text { DFAD [11] } & & & 93.3 \% \\ & \text { Adaptive DeepInversion [55] } &&& 93.26 \% \\ \hline \text { ResNet-18 } & \text { Ours } & \mathcal{L}_{\text {Inc }} & \mathcal{L}_{\mathrm{M}} & \\ & \text { •inceptionism } & \checkmark & & 77.31 \% \\ & \text { •moment matching } & & \checkmark & 94.61 \% \\ & \text { •both } & \checkmark & \checkmark & \mathbf{9 5 . 0 2 \%} \\ \hline \end{array} Model ResNet-34 ResNet-18 ResNet-18 ResNet-18 ResNet-18 Method Supervised Training Supervised Training Knowledge Distillation [23] Gaussian Noise DAFL [5] DFAD [11] Adaptive DeepInversion [55] Ours •inceptionism •moment matching •both LInc ✓✓LM✓✓ Accuracy 95.05%†93.92%‡94.34%‡11.43%92.22%93.3%93.26%77.31%94.61%95.02%
DAFL和Adaptive DeepInversion这两篇文章我有大概看过,感觉这两篇的含金量比较高。前者是19年的文章,比较早,和这篇文章的差别就在1. DAFL对生成器和学生模型迭代训练。2. DAFL的损失函数稍微落后一点,没用到Moment Loss这一项,而是用“特征图的点亮程度“来约束教师网络的中间过程。 ADI是和这篇文章同时期的文章,早了六个月,和这篇文章的区别在于:没有用生成器网络,而是用教师网络类似DeepDream的方法来生成图片,而其他的,像损失函数啥的都差不多。
CIFAR-100
CIFAR-100所用的生成器结构与CIFAR-10一样,但它的类别数比CIFAR-10更多,为了避免“模式崩溃”,这篇文章直接采用了100个生成器,每一个生成器生成一种类别。每个生成器Moment Loss的均值和方差都是不一样的,对应CIFAR-10每一个类别的均值方差。而教师网络有的只有整个数据集的均值方差,每一类的均值方差是无法得到的。这篇文章给出了一种扯淡的方法:1. 通过其他文献(训练输入噪声的)data-free的方法,每个类别都训一点;2. 拿上面的训出来图片的均值方差作为每个生成器的Moment Loss中的参数。
最后结果如下:
Model Method Accuracy ResNet-34 Supervised Training 77.26 % † ResNet-18 Supervised Training 76.53 % ‡ ResNet-18 Knowledge Distillation [23] 76.87 % ‡ ResNet-18 Gaussian Noise 1.23 % DAFL [5] 74.47 % DFAD [11] 67.7 % ResNet-18 Ours ∙ single generator 76.42 % ∙ ensembles (meta-data) 77.16 % ∙ ensembles (data-free) 77.02 % \begin{array}{llr} \hline \text { Model } & \text { Method } & \text { Accuracy } \\ \hline \text { ResNet-34 } & \text { Supervised Training } & 77.26 \%^{\dagger} \\ \text { ResNet-18 } & \text { Supervised Training } & 76.53 \%^{\ddagger} \\ \text { ResNet-18 } & \text { Knowledge Distillation [23] } & 76.87 \%^{\ddagger} \\ \hline \text { ResNet-18 } & \text { Gaussian Noise } & 1.23 \% \\ & \text { DAFL [5] } & 74.47 \% \\ & \text { DFAD [11] } & 67.7 \% \\ \hline \text { ResNet-18 } & \text { Ours } & \\ & \bullet \text { single generator } & 76.42 \% \\ & \bullet \text { ensembles (meta-data) } & 77.16 \% \\ & \bullet \text { ensembles (data-free) } & 77.02 \% \\ \hline \end{array} Model ResNet-34 ResNet-18 ResNet-18 ResNet-18 ResNet-18 Method Supervised Training Supervised Training Knowledge Distillation [23] Gaussian Noise DAFL [5] DFAD [11] Ours ∙ single generator ∙ ensembles (meta-data) ∙ ensembles (data-free) Accuracy 77.26%†76.53%‡76.87%‡1.23%74.47%67.7%76.42%77.16%77.02%
可以看到提升还是很明显的,即使是单个生成器(不用流氓办法),效果也是不错的。
ImageNet
ImageNet所采用的生成器网络模型如下:
z ∈ R 512 ∼ N ( 0 , I ) Linear ( 512 ) → 7 × 7 × 64 Reshape, BN, LeakyReLU Upsample × 2 3 × 3 Conv 64 → 64 , BN, LeakyReLU 3 × 3 Conv 64 → 3 , Tanh \begin{gathered} \hline z \in \mathbb{R}^{512} \sim \mathcal{N}(0, I) \\ \hline \text { Linear }(512) \rightarrow 7 \times 7 \times 64 \\ \hline \text { Reshape, BN, LeakyReLU } \\ \hline \text { Upsample } \times 2 \\ \hline 3 \times 3 \text { Conv } 64 \rightarrow 64, \text { BN, LeakyReLU } \\ 3 \times 3 \text { Conv } 64 \rightarrow 3, \text { Tanh } \\ \hline \end{gathered} z∈R512∼N(0,I) Linear (512)→7×7×64 Reshape, BN, LeakyReLU Upsample ×23×3 Conv 64→64, BN, LeakyReLU 3×3 Conv 64→3, Tanh
因为存储的关系,这里将输入数据从1024维降低到512维。最后一共有三个实验结果:
- ResNet-50,与其他文献横向对比。
Method Top-1 Acc. Δ Acc. Supervised Training 75.45 % ( 77.26 % † ) N/A BigGAN [4] 64.0 % ‡ − 13.26 % DeepInversion [55] 68.0 % − 9.26 % Ours 69.75 % − 5.70 % \begin{array}{lrr} \hline \text { Method } & \text { Top-1 Acc. } & \Delta \text { Acc. } \\ \hline \text { Supervised Training } & 75.45 \%\left(77.26 \%^{\dagger}\right) & \text { N/A } \\ \hline \text { BigGAN [4] } & 64.0 \%^{\ddagger} & -13.26 \% \\ \text { DeepInversion [55] } & 68.0 \% & -9.26 \% \\ \hline \text { Ours } & 69.75 \% & -5.70 \% \end{array} Method Supervised Training BigGAN [4] DeepInversion [55] Ours Top-1 Acc. 75.45%(77.26%†)64.0%‡68.0%69.75%Δ Acc. N/A −13.26%−9.26%−5.70% - ResNet-34为教师网络,ResNet-18为学生网络,不同生成器个数对应的准确率。
Model Method Top-1 ResNet-34 Supervised Training 59.68 % ResNet-18 Supervised Training 54.99 % ResNet-18 Ours -generators = 1 15.85 % -generators = 100 29.40 % -generators = 1000 51.82 % \begin{array}{llr} \hline \text { Model } & \text { Method } & \text { Top-1 } \\ \hline \text { ResNet-34 } & \text { Supervised Training } & 59.68 \% \\ \hline \text { ResNet-18 } & \text { Supervised Training } & 54.99 \% \\ \hline\text { ResNet-18 } & \text { Ours } & \\ & \text { -generators }=1 & 15.85 \% \\ & \text { -generators }=100 & 29.40 \% \\ & \text { -generators }=1000 & 51.82 \% \\ \hline \end{array} Model ResNet-34 ResNet-18 ResNet-18 Method Supervised Training Supervised Training Ours -generators =1 -generators =100 -generators =1000 Top-1 59.68%54.99%15.85%29.40%51.82% - ResNet-50为教师网络,不同学生网络的准确率。
Student Sup. Acc. Distill. Acc. Δ Acc. ResNet-50 75.45 % 69.75 % − 5.70 % ResNet-18 68.45 % 54.66 % − 13.79 % MobileNetV2 [49] 70.01 % 43.15 % − 26.86 % \begin{array}{lrrr} \hline \text { Student } & \text { Sup. Acc. } & \text { Distill. Acc. } & \Delta \text { Acc. } \\ \hline \text { ResNet-50 } & 75.45 \% & 69.75 \% & -5.70 \% \\ \text { ResNet-18 } & 68.45 \% & 54.66 \% & -13.79 \% \\ \text { MobileNetV2 [49] } & 70.01 \% & 43.15 \% & -26.86 \% \\ \hline \end{array} Student ResNet-50 ResNet-18 MobileNetV2 [49] Sup. Acc. 75.45%68.45%70.01% Distill. Acc. 69.75%54.66%43.15%Δ Acc. −5.70%−13.79%−26.86%