自然语言处理——序列模型
本文主要写些关于常见序列模型的一些理解,主要是为了记录一下,自己对这几个模型的理解还远远不够。
HMM 隐马尔可夫模型
马尔可夫性是指当前状态t 只和前一状态t-1相关(一阶),和之前t-2之前的就不相关,这个也算是n-gram语言模型吧,都是为了控制模型复杂度(一方面模型过于复杂,数据集不够会导致模型达不到收敛;另外一方面模型复杂度成指数增长的话,硬件和时间都是不能接受的)。
隐马尔可夫模型,指定隐含状态满足一阶马尔可夫,而观测是由单个隐含状态决定的。

模型主要参数就包括: 隐含状态之间的转移矩阵,和隐含状态到发射概率的发射概率矩阵,以及隐含状态初始概率。
如果把序列标注问题完全按照分类来做,也就是单独来看每个字的分类,然后使用生成模型来建模。 那么我们参数模型仍然包括, 隐含状态的分布 和隐含状态下观测的条件概率。
而序列任务,明显i1和i2是相关的。而使用马尔可夫性来简化建模序列模型,将之前的隐含状态的分布 转换为 隐含状态初始概率和转移矩阵。利用转移矩阵就考虑了i1和i2的相关性。 (比如从i1(B_N)到i2(E_V)的转移矩阵为0,那么就不可能出现"B_N,E_V"这样的序列)
HMM的问题主要分为
- 已知模型,和观测序列, 计算某个隐含序列的概率
- 已知观测序列,求解模型
- 已知模型和观测序列,计算最可能的隐含序列
其分别使用了前向算法、维特比算法(使用动态规划的方法来解决问题)最大似然、Baum-Welch算法。(Baum-Welch算法类似EM算法,具体我不懂)
MEMM算法
最大熵模型
ME模型主要是在保证特征 f f f的期望应该和从训练数据中得到的特征期望一致的条件下,使得条件熵最大。
m i n − H ( P ) = ∑ x , y p ^ ( x , y ) f ( x , y ) min -H(P)=\sum_{x,y}\hat{p}(x,y)f(x,y) min−H(P)=x,y∑p^(x,y)f(x,y)
s . t . ∑ x , y p ^ ( x ) P ( y ∣ x ) f i ( x , y ) = τ i s.t.\ \ \sum_{x,y}\hat{p}(x)P(y|x)f_i(x,y)=\tau_i s.t. x,y∑p^(x)P(y∣x)fi(x,y)=τi
∑ x P ( y ∣ x ) = 1 \sum_xP(y|x)=1 x∑P(y∣x)=1
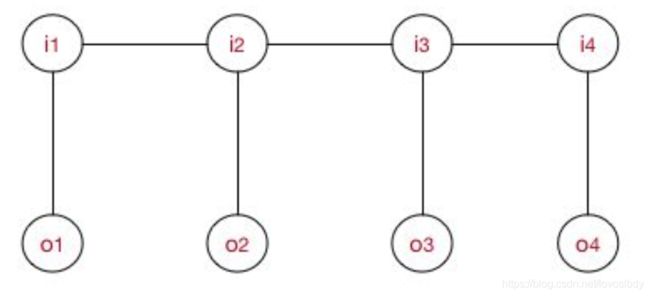
MEMM算法如下图所示
MEMM与HMM首先不同的是,这里箭头是从观测序列指向隐含序列(这里不是生成模型,不存在隐含序列,就是从X指向Y)在相同的序列标注任务中(X即词语,Y即对应的标签)
其建模概率为:

其中

求解模型主要是获取 λ \lambda λ的权重。已知权重便可以使用上图的公式, 计算出 已知O,I的转移矩阵。这里I的转移矩阵是和O相关的。另外这里可以添加很多特征,比如 i-2,i-3,其肯定就保证了更长的信息区间。
为什么叫做最大熵
这个我没有看懂,看知乎说因为这里P(Y|X)使用了最大熵分类器的形式,但是我没有看出来该公式和最大熵模型的联系。。
具体计算
具体其求解序列标注三类问题和HMM很类似。由于其有马尔可夫性,还是用动态规划的思路求解。
然后就是其存在标注偏置的问题。

如图的转移矩阵:状态1倾向于转换到状态2,同时状态2倾向于保留在状态2。
具体计算出来最优路径(累乘最大)是P(1-> 1-> 1-> 1)= 0.4 x 0.45 x 0.5 = 0.09 ,
其余的
P(2->2->2->2)= 0.2 X 0.3 X 0.3 = 0.018,
P(1->2->1->2)= 0.6 X 0.2 X 0.5 = 0.06,
P(1->1->2->2)= 0.4 X 0.55 X 0.3 = 0.066
那么为什么会产生偏置呢?局部归一化?但是
- 状态1倾向于转换到状态2,同时状态2倾向于保留在状态2。这个意味着什么?意味着最优路径的终点肯定是2?
- 这个和viterbi算法优化有关系么?
这里贴上知乎截图,没有看懂。。。。但是我感觉局部归一化是有问题的。

CRF算法
CRF和前面最大区别就是其是无向图,所以其计算概率的方式不一样,所以其可以避免标签偏置的问题。
具体其建模为

感觉上和MEMM最大的区别就在于其归一化在最外面,而MEMM是归一化之后再累乘的。(因为无向图和有向图的区别?)
具体求解出 λ \lambda λ之后,便可以计算序列的概率。
LSTM+CRF
现在神经网络后面接CRF已经成为标配了。
参考LSTM+CRF
具体看LSTM之后接的CRF,其将LSTM输出的标签当作自身(Ii)特征分数,一个转移矩阵(Ii-1到Ii)充当相邻特征分数,其目标函数就是实际序列概率最大。
主要是记录自己的想法,理解极其不透彻,欢迎指正!!
