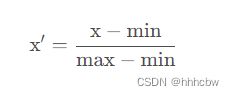sklearn包使用Extra-Trees和GridSearchCV完成成人死亡率预测

成年人死亡率指的是每一千人中 15 岁至 60 岁死亡的概率（数学期望）。这里我们给出了世界卫生组织（WHO）下属的全球卫生观察站（GHO）数据存储库跟踪的所有国家健康状况以及许多其他相关因素。要求利用训练数据建立回归模型，并预测成年人死亡率（Adult Mortality）。

---

导入相关包

import pandas as pd
import sklearn
import numpy as np

from sklearn.impute import SimpleImputer
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error, r2_score

import joblib

训练数据读取和可视化

训练数据链接：https://pan.baidu.com/s/1KYtUoHBIv1pqYDbO9OdDHg?pwd=nefu
提取码：nefu

训练数据（train_data.csv）总共包含 2336 条记录，22 个字段，主要字段说明如下：

• Country：国家
• Year：年份
• Status：发达国家或发展中国家
• Life expectancy：预期寿命
• Infant deaths：每千人口中的婴儿死亡人数
• Alcohol：人均酒精消费量（以升纯酒精为单位）
• percentage expenditure：卫生支出占人均国内生产总值的百分比
• Hepatitis B：一岁儿童乙型肝炎免疫疫苗接种率
• Measles：麻疹每 1000 人报告的病例数
• BMI：所有人群平均 BMI 指数
• under-five deaths：每千人口中五岁以下死亡人数
• Polio：1 岁儿童脊髓灰质炎免疫覆盖率（%）
• Total expenditure：政府卫生支出占政府总支出的百分比
• Diphtheria：1 岁儿童白喉、破伤风类毒素和百日咳免疫接种率（%）
• HIV/AIDS：每千名活产婴儿死于艾滋病毒/艾滋病（0-4 岁）
• GDP：人均国内生产总值（美元）
• Population：人口
• thinness 1-19 years：10 至 19 岁儿童和青少年的消瘦流行率
• thinness 5-9 years：5 至 9 岁儿童中的消瘦流行率
• Income composition of resources：财力收入构成方面的人类发展指数（从 0 到 1）
• Schooling：受教育年限
• Adult Mortality：成人死亡率（每 1000 人中 15 至 60 岁死亡的概率）
  测试数据(test_data.csv)总共包含 592 条记录，21 个字段，和训练数据相比，除了不包含 Adult Mortality 字段外，其他完全相同。

需要注意的是数据中可能会有一些字段的值存在缺失。

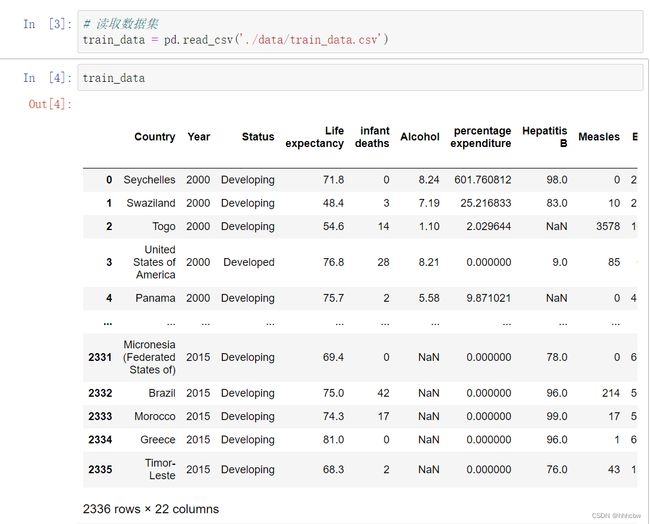
# 读取数据集
train_data = pd.read_csv('./data/train_data.csv')

train_data

可以看到 NaN 就是有缺失值。

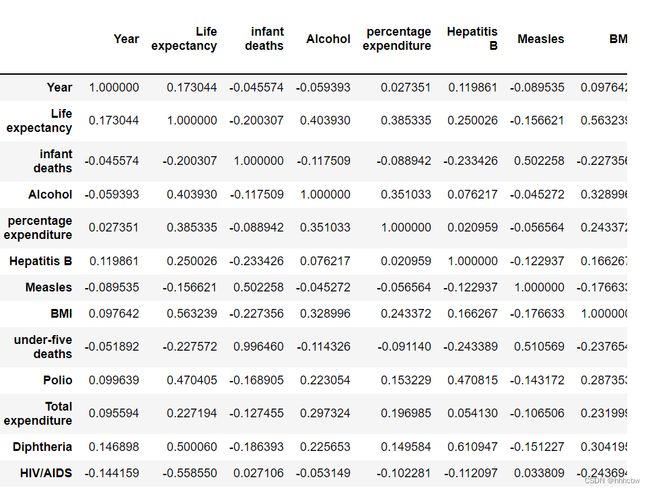
下面计算各个特征之间的皮尔森相关系数，皮尔森相关系数可以理解为特征与特征之间的线性相关程度，取值[-1,1]，正数就是正相关，负数就是负相关。且绝对值越大，即越接近1，相关程度越高。具体可以看这篇文章。

# 计算各个特征之间的皮尔森相关系数
train_data.corr()

# 将相关性矩阵绘制成热力图
corr = train_data.corr()
corr.style.background_gradient(cmap='coolwarm')

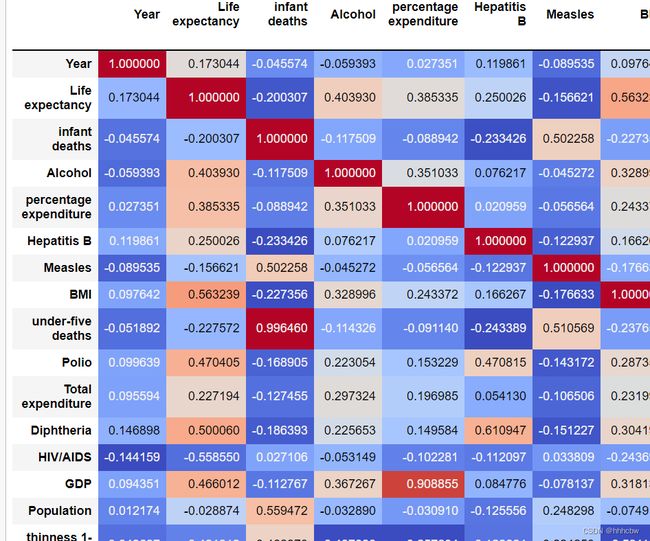
从热力图可以看出 infant deaths 与 under-five deaths有很强的正相关，即 每千人口中的婴儿死亡人数 与 每千人口中五岁以下死亡人数 有很强的正相关。其实很好理解，因为正常情况下，under-five deaths 包含了 infant deaths 的情况，那后面我们就可以考虑将 infant deaths 这个属性去除掉。

除此之外，也可以看到 thinness 1-19 years 和 thinness 5-9 years 有很强的正相关，也是和上面一样的道理。

可以用 seaborn 可视化数据之间的依赖关系：

import seaborn as sns
sns.pairplot(train_data)

模型拟合和成年人死亡率预测

train_data = pd.read_csv('./data/train_data.csv') # 训练数据
model_filename = './model.pkl'  # 模型路径
imputer_filename = './imputer.pkl' # 缺失值处理器路径
scaler_filename = './scaler.pkl' #  归一化处理器路径
# 划分为训练集和测试集![请添加图片描述](https://img-blog.csdnimg.cn/2920c38856524604b57fb8dcf17d5ac1.png)

train_y = train_data.iloc[:,-1].values
train_data = train_data.drop(["Adult Mortality"], axis=1)
x_train, x_test, y_train, y_test = train_test_split(train_data, train_y, random_state=666, test_size=0.25)

因为每个属性其取值范围差异巨大，无法直接比较。所以需要归一化把有量纲表达式变成无量纲表达式，便于不同单位或量级的指标能够进行比较和加权。

这里使用最小最大归一化

# 预处理数据，进行数据归一化，以及补充缺失值
def preprocess_data(data, imputer=None, scaler=None):
    
    column_name = ['Year', 'Life expectancy ', 'infant deaths', 'Alcohol',
               'percentage expenditure', 'Hepatitis B', 'Measles ', ' BMI ', 'under-five deaths ',
               'Polio', 'Total expenditure', 'Diphtheria ', ' HIV/AIDS', 'GDP', 'Population',
               ' thinness  1-19 years', ' thinness 5-9 years', 'Income composition of resources',
               'Schooling']
    data = data.drop(["Country", "Status"], axis=1)
    
    if imputer==None: # 采用均值填充缺失值
        imputer = SimpleImputer(strategy='mean', missing_values=np.nan)
        imputer = imputer.fit(data[column_name])
    data[column_name] = imputer.transform(data[column_name])
    
    if scaler==None: # 采用最小最大归一化
        scaler = MinMaxScaler()
        scaler = scaler.fit(data)
    data_norm = pd.DataFrame(scaler.transform(data), columns=data.columns)
    
    data_norm = data_norm.drop(['Year', 'infant deaths', 'thinness 5-9 years'], axis = 1)
    
    return data_norm, imputer, scaler

下面使用训练数据对模型进行训练，注意这里使用了 ExtraTreesRegressor 作为回归模型，并使用了 GridSearchCV 进行参数网格搜索。使用ExtraTreesRegressor 是因为发现其他方法过过拟合很严重

Extra-Trees 为极端随机数(Extremely randomized tress)，其与随机森林区别如下：

1. RF应用了Bagging进行随机抽样，而ET的每棵决策树应用的是相同的样本。

2. RF在一个随机子集内基于信息熵和基尼指数寻找最优属性，而ET完全随机寻找一个特征值进行划分。

在 sklearn 包中有如下参数：

参数	说明
n_estimators:int, default=100	森林中树的数量
criterion: {“squared_error”,“absolute_error”},default=“squared_error”	计算划分标准的方法默认为均方误差
max_depth:int,default=None	树的最大深度，如果不设置节点将会一直扩展到所有叶子都是纯净的或则直到所有叶子都包含少于 min_samples_split 的样本
min_samples_split:int or float,default=2	代表如果要划分节点当前节点的最小样本数，如果指定为整型，最小数量就是min_samples_split，如果指定为浮点型，则最小数量就是 ceil(min_samples_split*n_samples) n_samples为总的样本数
min_samples_leaf: int or float, default=1	代表如果要划分当前节点，划分出的子节点的样本数量不能小于 min_samples_leaf
bootstrap:bool,default=False	表示训练数据采样是否放回
oob_score:bool,default=False	表示是否使用包外样本评估泛化分数，仅当bootstrap=True可用
random_state:int, RandomState instance or None,default=None	随机数的种子
verbose:int,default=0	为1训练和测试输出详细信息
max_samples: int or float,default=None	表示每次采样的样本数量
n_jobs:int,default=None	表示并行工作的数量，-1使用所有核心

其他参数可用看官方文档。

然后我们就可以根据这些参数进行 GridSearchCV 参数网格搜索，这里的GridSearch代表网格搜索，CV 代表crossvalidation交叉验证，GridSearchCV 可以保证在指定的参数范围内找到精度最高的参数，其参数说明如下：

参数	说明
estimator:estimator object	模型
para_grid:dict or list of dictionaries	参数网格
refit:bool, str,or callable,default=True	是否使用最优参数在整个数据集上重新拟合
cv:int, cross-validation generator or an iterable,default=None	决定交叉验证策略，默认为5-fold验证
verbose:int	>1显示每次验证计算时间以及参数列表;>2显示分数;>3折和候选参数索引与计算开始时间被显示

def gridsearch_cv(train_data):
    # 需要网格搜索的参数
    n_estimators = [i for i in range(200,401,10)]
    max_depth = [i for i in range(5, 11)]
    min_samples_split = [i for i in range(2, 8)]
    min_samples_leaf = [i for i in range(1,7)]
    max_samples = [i/100 for i in range(95, 100)]
    parameters = {'n_estimators':n_estimators,
                   'max_depth':max_depth, 
                    'min_samples_split':min_samples_split, 
                   'min_samples_leaf':min_samples_leaf,
                    'max_samples':max_samples}
    regressor = ExtraTreesRegressor(bootstrap=True, oob_score=True, random_state=1)
    gs = GridSearchCV(regressor, parameters, refit = True, cv = 5, verbose = 1, n_jobs = -1)
    x_train_norm, imputer, scaler = preprocess_data(x_train)

    train_x_norm = x_train_norm.values
    gs.fit(x_train_norm,y_train)
    
    joblib.dump(gs, model_filename)
    joblib.dump(imputer, imputer_filename)
    joblib.dump(scaler, scaler_filename)
    return gs

gs_model = gridsearch_cv(x_train, y_train)
print('最优参数: ',gs.best_params_)
print('最佳性能: ', gs.best_score_)

模型已经找到最优参数，且训练完成，保存模型文件至本地。

下面加载模型在测试集上进行测试：

def predict(x_test):
    loaded_model = joblib.load(model_filename)
    imputer = joblib.load(imputer_filename)
    scaler = joblib.load(scaler_filename)

    x_test_norm, _, _ = preprocess_data(x_test, imputer, scaler)
    test_x_norm = x_test_norm.values
    predictions = loaded_model.predict(test_x_norm)
    
    return predictions

y_pred = predict(x_test)
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
print("MSE is {}".format(mse))
print("R2 score is {}".format(r2))

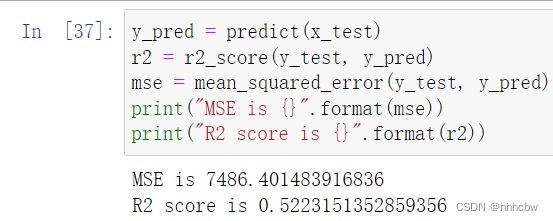
这里一共使用了两个指标，MSE(均方误差代表了预测值与真实值之间的差异)，R² 衡量了模型与基准模型(取平均值)之间的差异，其计算公式如下：

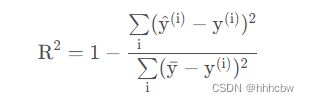
分子代表预测值和真实值之间的差异，分母代表均值与真实值的差异，所以R²越接近1，代表模型相对于基准模型与真实值差异越小，即模型越好。当R²<0，说明模型还不如基准模型。

---

学习曲线

学习曲线就是通过画出不同训练集大小时训练姐和交叉验证的准确率，可以看到模型在新数据上的表现，进而来判断模型是否 方差偏高 或 偏差偏高，以及增大训练集是否可以减小过拟合。

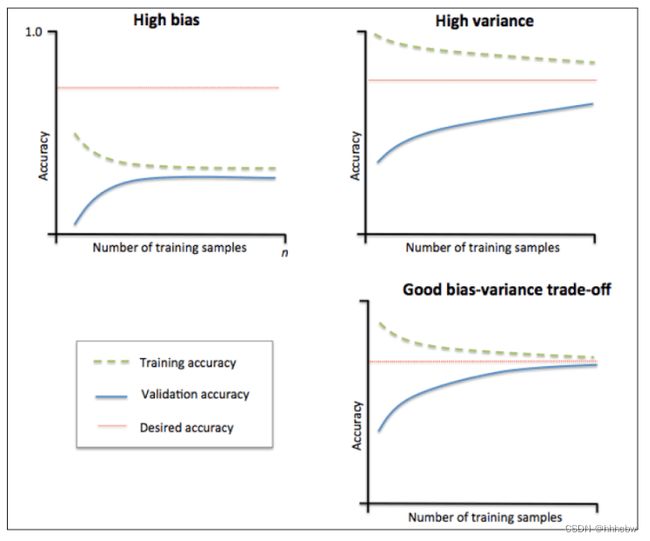
当训练集和测试集的误差收敛但却很高时，为高偏差。
左上角的偏差很高，训练集和验证集的准确率都很低，很可能是欠拟合。
我们可以增加模型参数，比如，构建更多的特征，减小正则项。
此时通过增加数据量是不起作用的。

当训练集和测试集的误差之间有大的差距时，为高方差。
当训练集的准确率比其他独立数据集上的测试结果的准确率要高时，一般都是过拟合。
右上角方差很高，训练集和验证集的准确率相差太多，应该是过拟合。
我们可以增大训练集，降低模型复杂度，增大正则项，或者通过特征选择减少特征数。

理想情况是是找到偏差和方差都很小的情况，即收敛且误差较小。

绘制学习曲线代码如下：
plot_learning_curve.py

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import learning_curve
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import ShuffleSplit

import joblib

# 预处理数据，进行数据归一化，以及补充缺失值
def preprocess_data(data, imputer=None, scaler=None):
    
    column_name = ['Year', 'Life expectancy ', 'infant deaths', 'Alcohol',
               'percentage expenditure', 'Hepatitis B', 'Measles ', ' BMI ', 'under-five deaths ',
               'Polio', 'Total expenditure', 'Diphtheria ', ' HIV/AIDS', 'GDP', 'Population',
               ' thinness  1-19 years', ' thinness 5-9 years', 'Income composition of resources',
               'Schooling']
    data = data.drop(["Country", "Status"], axis=1)
    
    if imputer==None: # 采用均值填充缺失值
        imputer = SimpleImputer(strategy='mean', missing_values=np.nan)
        imputer = imputer.fit(data[column_name])
    data[column_name] = imputer.transform(data[column_name])
    
    if scaler==None: # 采用最小最大归一化
        scaler = MinMaxScaler()
        scaler = scaler.fit(data)
    data_norm = pd.DataFrame(scaler.transform(data), columns=data.columns)
    
    data_norm = data_norm.drop(['Year', 'infant deaths', ' thinness 5-9 years'], axis = 1)
    
    return data_norm, imputer, scaler

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    """
    画出data在某模型上的learning curve.
    参数解释
    ----------
    estimator : 你用的分类器。
    title : 表格的标题。
    X : 输入的feature，numpy类型
    y : 输入的target vector
    ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
    cv : 做cross-validation的时候，数据分成的份数，其中一份作为cv集，其余n-1份作为training(默认为3份)
    n_jobs : 并行的的任务数(默认1)
    """
    plt.figure()
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    plt.grid()

    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")

    plt.legend(loc="best")
    plt.draw()
    plt.show()

	# 中间值
    midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
    # 最大最小差异
    diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
    return midpoint, diff

if __name__ == '__main__':
	train_data = pd.read_csv('./data/train_data.csv') # 训练数据
	model_filename = './model.pkl'  # 模型路径
	imputer_filename = './imputer.pkl' # 缺失值处理器路径
	scaler_filename = './scaler.pkl' #  归一化处理器路径
	train_y = train_data.iloc[:,-1].values
	train_data = train_data.drop(["Adult Mortality"], axis=1)
	x_train, x_test, y_train, y_test = train_test_split(train_data, train_y, random_state=666, test_size=0.25)
	imputer = joblib.load(imputer_filename)
	scaler = joblib.load(scaler_filename)
	
	train_x_norm, _, _ = preprocess_data(x_train, imputer, scaler)
	train_x = train_x_norm.values
	title = "Learning Cures (Extra-Trees)"
	# Cross validation with 100 iterations to get smoother mean test and train
	# score curves, each time with 20% data randomly selected as a validation set.
	cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
	
	plot_learning_curve(ExtraTreesRegressor(max_depth=10, max_samples=0.97, min_samples_leaf=2, min_samples_split=2, n_estimators=360), title, train_x, y_train, ylim=(0.3,1.01), cv=cv, n_jobs=-1)