数学模型-插值与拟合matlab实现

插值与拟合模型(一)----水道测量问题

Matlab的一维插值函数为interp1()， 调用格式为：

yy=interp1(x,y,xx,方法) 其中x=[x1,x2,…,xn]’, y=[y1,y2,…,yn]’,

两个向量分别为一组自变量和函数值
xx为待求插值点处横坐标， yy返回的对应纵坐标

插值方法可选用方式
’ linear’	线性插值
’ nearest’	最近邻等值方式
'cubic’	三次Hermite插值
’ spline’	三次样条插值

问题1 插值实验

Matlab程序chazhi1.m：

x=0:0.1:1;
y=(x.^2-3*x+7).*exp(-4*x).*sin(2*x); %产生原始数据
subplot(1,2,1);%一行两个图，此处为第一个图
plot(x,y,x,y,'ro') %作图
xx=0:0.02:1; %待求插值点
yy=interp1(x,y,xx,'spline'); %此处可用nearest,cubic,spline分别试验
%或yy=spline(x,y,xx);
subplot(1,2,2)%一行两个图，此处为第二个图
plot(x,y,'ro',xx,yy,'b') %作图

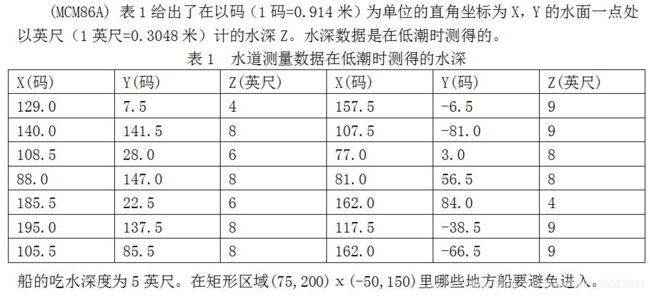
问题2 水道测量问题

解答：
所给14个点平面散点图， 其中有两点不在区域： (75,200)ⅹ (-50,150)

反距离权重法 (IDW)算法

设有 $n$ 个点 $\left(x_i,y_i,z_i\right)$, 计算平面上任意点 $(x,y)$ 的 $z$ 值。
$$z=\sum _{i=1}^n{w}_i\cdot z_i$$
其中权重: $w_i=\frac{1/d_i^p}{{\sum }_{i=1}^{n}1/d_i^p},d_i=\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}$

当 $p$ 越大, 则当 $\left(x_i,y_i\right)$ 距离 $(x,y)$ 越近, 其相对作用越大，越远相对作用越小。
这里取 $p=3$ 。
按照 IDW 方法, 对 $x$ 方向和 $y$​​ 方向都按照间隔 1 进行剖分。 得到的水底河床图及等值线图

Matlab程序如下：

clear; %AMCM86A
data=[129.0,7.5,4;
140.0,141.5,8;
108.5,28.0,6;
88.0,147.0,8;
185.5,22.5,6;
195.0,137.5,8;
105.5,85.5,8;
157.5,-6.5,9;
107.5,-81.0,9;
77.0,3.0,8;
81.0,56.5,8;
162.0,84.0,4;
117.5,-38.5,9;
162.0,-66.5,9];%水道测量数据
plot(data(:,1),data(:,2),'*')
xx=[75,-50;
200,-50;
200,150;
75,150;
75,-50];
hold on;
plot(xx(:,1),xx(:,2),'r')
xlabel('X');
ylabel('Y');
title('水道离散点平面图');
pause
d=zeros(14,1);
w=zeros(14,1);
p=3; %参数p
[X,Y]=meshgrid(75:1:200,-50:1:150);
%对(X,Y)进行网格剖分
Z=zeros(size(X));
[m,n]=size(X);
tp=0;
for i=1:m
for j=1:n
for k=1:14
%(x,y)格点到各已知各点距离
d(k)=sqrt((X(i,j)-data(k,1))^2+(Y(i,j)-data(k,2))^2);
w(k)=1.0/d(k)^p;%各点权重
end;
s=sum(w);
w=w/s;%权值归一化
z=sum(data(:,3).*w);
%加权求和
Z(i,j)=-z;
if z<=5
tp=tp+1;
D(tp,1)=X(i,j); D(tp,2)=Y(i,j);
%获得水深低于5英尺的点
end
end
end
subplot(2,1,1);
surf(X,Y,Z) %作曲面图
xlabel('X'); ylabel('Y'); zlabel('Z');
title('水道测量水底形状图');
subplot(2,1,2);
contour(X,Y,Z); %作等值线图
hold on
plot(D(:,1),D(:,2),'*')%作出水深低于5英尺的点
xlabel('X'); ylabel('Y');
title('水道测量等值线图');
grid on
hold off

插值与拟合模型(二)-----水塔流量问题

（ MCM91A） 美国某洲的各用水管理机构要求各社区提供以每小时多少加仑计的用水率，以及每天总的用水量，但许多社区并没有测量水流入或流出水塔水量的设备，他们只能每小时测量水塔中的水位，精度在0.5%以内，更为重要的是，无论什么时候，只要水塔中的水位下降到某一最低水位L时，水泵就启动向水塔重新充水至某一最高水位H，但也无法得到水泵的供水量的测量数据。 水泵每天向水塔充水一次或两次， 每次约两小时。水塔是一个垂直圆形柱体， 高为40英尺， 直径57英尺。当水塔的水位降至27.00英尺时开始向水塔充水，当水位升至35.50英尺时停止充水。

试估计在任何时刻, 甚至包括水泵正在工作期间内, 水从水塔流出的流量 $f(t)$, 并估计一天的总用水量, 表 1 中给出了某个真实小镇某一天的真实数据。

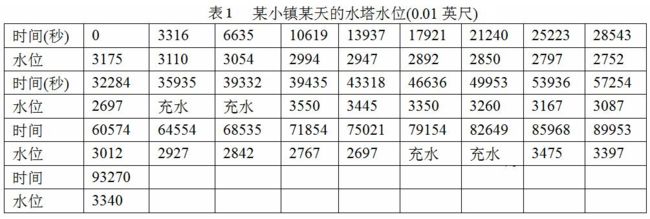
解答:

1. 水塔充水时间的确定
   (1) 第一次充水时间： t=32284到t=39435秒， 间隔dt=1.9864小时
   (2) 第二次充水时间： t=75021到t=82649秒， 间隔dt=2.1189小时
2. 计算各时刻塔内水的体积
   单位转换为1英尺=0.3048米, 1升=1/3.785411加仑
   体积计算公式为$v=\pi \cdot d^{2}h/4$​

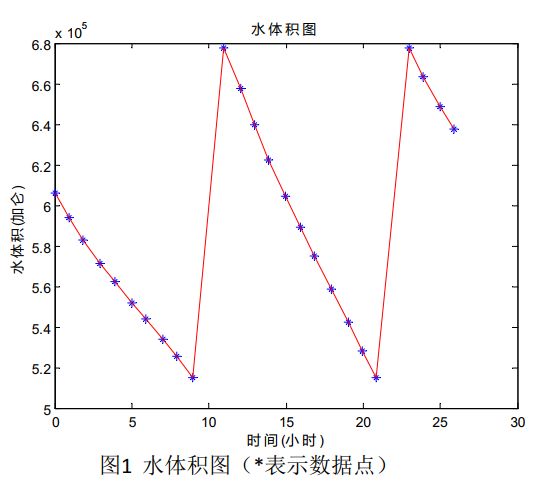
3.计算各时刻点的水流量(加仑/小时)

水流量公式为: $f(t)=\left|\frac{dv(t)}{dt}\right|$​

25 个时刻处的水流量采用差分的方法得到，共分三段分别处理

差分公式为：

(1) 对每段前两点采用向前三点差分公式
$$f\left(t_i\right)=\left|\frac{-3V_i+4V_{i+1}-V_{i+2}}{2\left(t_{i+1}-t_i\right)}\right|$$
(2) 对每段最后两点采用向后三点差分公式
$$f\left(t_i\right)=\left|\frac{3V_i-4V_{i-1}+V_{i-2}}{2\left(t_i-t_{i-1}\right)}\right|$$
(3) 对每段中间点采用中心差分公式
$$f\left(t_i\right)=\left|\frac{-V_{i+2}+8V_{i+1}-8V_{i-1}+V_{i-2}}{12\left(t_{i+1}-t_i\right)}\right|$$
计算各点水流量见表3.

4.用三次样条拟合流量数据
对表3中25个时刻点流量数
据采用三次样条插值见图6

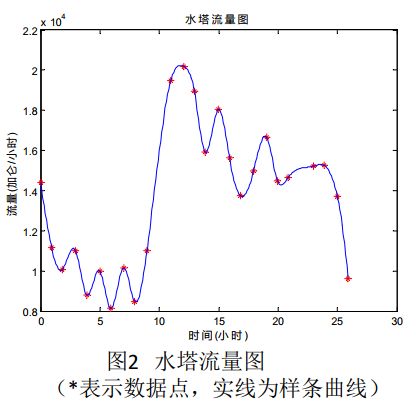
5.**一天总用水量计算 **

方法 1:直接积分法:

$S_1={\int }_0^{24}f(t)dt=332986($ 加仑） \quad

\quad ​​ 设样条揷值得 $\mathrm{n}$​​ 个点 $y_1,y_2,\dots ,y_n$​​, 间隔为 $h$​​ 数值积分公式: $S=\left[y_1+y_n+2\left(y_2+\dots +y_{n-1}\right)\right]\cdot \frac{h}{2}$​

方法2：分段计算

第一次充水前用水 $V_1=606125-514872=91253$​​​​ (加仑)

第二次充水前用水 $V_2=677715-514872=162843$​​( 加仑 $)$​

$[22.9581,23.88]$​​ 期间用水 $V_3=677715-663397=14318$​​ (加仑 )

第一次充水期间用水: $V_4={\int }_{8.9678}^{10.9542}f(t)dt=30326$​ (加仑)

第二次充水期间用水: $V_5={\int }_{20.8392}^{22.9581}f(t)dt=31605$​​( 加仑 )

$[23.88,24]$期间用水: $V_6={\int }_{23.88}^{24}f(t)dt=1524$​​​​​​​​ (加仑)

总共用水 $S_2={\sum }_{i=1}^6{V}_i=33186$ (加仑)

两种方法误差 $\mathrm{err}=\left|\frac{S_1-S_2}{S_1}\right|=0.34\%$

6.水泵流量计算

第一次充水期间水塔体积增加	充水时间	第一次充水期间水泵平均流量
$\Delta V_1=677715-514872=162843$(加仑)	$\Delta t_1=10.9542-8.9678=1.9864$( 小时 )	$ p_{1}=\frac{\Delta V_{1}+\int_{8.9678}^{10.9542} f(t) d t}{\Delta t_{1}}=97246$(加仑/小时)

第二次充水期间水塔体积增加	充水时间	第二次充水期间水泵平均流量
$\Delta V_2=677715-514872=162843$(加仑)	\quad $\Delta t_2=22.9581-20.8392=2.1189$(小时 )	$p_2=\frac{\Delta V_2+{\int }_{20.8392}^{22.9581}f(t)dt}{\Delta t_2}=91769$( 加仑 小时 )

则整个充水期间水泵平均流量

$p=\left(p_1+p_2\right)/2=94507$​( 加仑 /小时 )

Matlab程序

%AMCM91A
c=0.3048; %1英尺等于0.3048米
p=1.0/3.785; %1升=1/3.785411加仑
d=57*c; %直径
h=31.75*c;
v=pi*d*d*h/4*1000*p;
data=[0,3175;
3316,3110;
6635,3054;
10619,2994;
13937,2947;
17921,2892;
21240,2850;
25223,2797;
28543,2752;
32284,2697;
39435,3550;
43318,3445;
46636,3350;
49953,3260;
53936,3167;
57254,3087;
60574,3012;
64554,2927;
68535,2842;
71854,2767;
75021,2697;
82649,3550;
85968,3475;
89953,3397;
93270,3340];%原始数据
t=data(:,1)/3600;%计算时间(小时为单位)
v=pi*d*d*data(:,2)/100*c/4*1000*p;%计算体积
%计算差分
n=length(v);
f=zeros(n,1); %存储差分值
%计算第一段
n1=10;
for i=1:n1
if i<=2 %前两点采用向前三点差分
f(i)=abs(-3*v(i)+4*v(i+1)-v(i+2))/(2*(t(i+1)-t(i)));
elseif i<=n1-2
%采用中心差分公式
f(i)=abs(-v(i+2)+8*v(i+1)-8*v(i-1)+v(i-2))/(12*(t(i+1)-t(i)));
elseif i>=n1-1 %后两点采用向后三点差分
f(i)=abs(3*v(i)-4*v(i-1)+v(i-2))/(2*(t(i)-t(i-1)));
end
end
n2=21; %计算第二段
for i=n1+1:n2
if i<=n1+2 %前两点采用向前差分
f(i)=abs(-3*v(i)+4*v(i+1)-v(i+2))/(2*(t(i+1)-t(i)));
elseif i<=n2-2
f(i)=abs(-v(i+2)+8*v(i+1)-8*v(i-1)+v(i-2))/(12*(t(i+1)-t(i)));
elseif i>=n2-1
f(i)=abs(3*v(i)-4*v(i-1)+v(i-2))/(2*(t(i)-t(i-1)));
end
end
n3=25; %计算第三段
for i=n2+1:n3
if i<=n2+2 %前两点采用向前差分
f(i)=abs(-3*v(i)+4*v(i+1)-v(i+2))/(2*(t(i+1)-t(i)));
elseif i<=n3-2
f(i)=abs(-v(i+2)+8*v(i+1)-8*v(i-1)+v(i-2))/(12*(t(i+1)-t(i)));
elseif i>=n3-1
f(i)=abs(3*v(i)-4*v(i-1)+v(i-2))/(2*(t(i)-t(i-1)));
end
end
plot(t,f,'r*'); %画原始点图
tmin=min(t); tmax=max(t);
tt=tmin:0.1:tmax; %获得离散的时间点,用于作样条曲线
ff=spline(t,f,tt); %计算三次样条插值
hold on
plot(tt,ff,'b'); %画样条曲线
xlabel('时间(小时)');
ylabel('流量(加仑/小时)');
title('水塔流量图');
hold off
dt=0.05;
t2=0.5:dt:24.5; %获得离散的时间点,用于积分
nn=length(t2);
f2=spline(t,f,t2);
%计算24小时用水量,采用复化梯形公式
s=(f2(1)+f2(nn)+2*sum(f2(2:nn-1)))*dt/2 ;
fprintf('(全部积分法)1天总水流量s= %8.2f\n',s);
%第一次水塔增加的水
v10=v(11)-v(10);
dt1=t(11)-t(10);
%第一次充水其间流出的水
tp=t(10):dt:t(11);
nn=length(tp);
yp=spline(t,f,tp); %计算三次样条插值
v11=(yp(1)+yp(nn)+2*sum(yp(2:nn-1)))*dt/2;
v1=v10+v11;%第一次充水总量
p1=v1/dt1; %第一次充水的平均水流量
%第二次水塔增加的水
v20=v(22)-v(21);
dt2=t(22)-t(21);
%第二次充水其间流出的水
tp1=t(21):dt:t(22);
nn=length(tp1);
yp1=spline(t,f,tp1); %计算三次样条插值
v21=(yp1(1)+yp1(nn)+2*sum(yp1(2:nn-1)))*d
v2=v20+v21;%第二次充水总量
p2=v2/dt2; %第二次充水的平均水流量
p=(p1+p2)/2; %两次充水平均水流量
fprintf('两次充水平均水流量p= %8.2f\n',p);
%第一次充水前总流量
vv1=v(1)-v(10);
%两次充水间总流量
vv2=v(11)-v(21);
% t=83649到85968其间流量
vv3=v(22)-v(23);
%第一次充水期间流量
ta=t(10):dt:t(11);
%获得离散的时间点,用于积分
nn=length(ta);
fa=spline(t,f,ta);
s1=(fa(1)+fa(nn)+2*sum(fa(2:nn-1)))*dt/2;
%第二次充水期间流量
tb=t(21):dt:t(22); %获得离散的时间点,用于积分
nn=length(tb);
fb=spline(t,f,tb);
s2=(fb(1)+fb(nn)+2*sum(fb(2:nn-1)))*dt/2;
%t=85968到86400流量
tc=t(23):dt:24; %获得离散的时间点,用于积分
nn=length(tc);
fc=spline(t,f,tc);
s3=(fc(1)+fc(nn)+2*sum(fc(2:nn-1)))*dt/2 ;
ss=vv1+vv2+vv3+s1+s2+s3;
fprintf('(部分积分法)1天总水流量ss= %8.2f\n',ss);
err=abs((s-ss)/s);
fprintf('两种计算法总量相对误差%6.2f%%\n',err*100);

程序计算结果为：
(全部积分法)1天总水流量s= 332986.22
两次充水平均水流量 p= 94507.48
(部分积分法)1天总水流量 ss= 331869.29
两种计算法总量相对误差 0.34%