HNSW算法(nsmlib/hnswlib)

一、数据结构

1、HierarchicalNSW类成员描述

成员	描述
num_deleted_	有过删除某向量的次数。 PS：不考虑增量情况下，它不会发生影响
M_	每个(非0层)节点可以有多少个邻居
maxM_	maxM_ = M_
maxM0_	第0层节点可以有多少个邻居 = 2 * maxM_
ef_construction_	潜在邻居列表，用于优选邻居
ef_	实际意义不大参数
data_size_	每条原始向量需占多少字节 =  dim * sizeof(float)
size_links_level0_	第0层节点的邻居表，需占多少字节 = maxM0_ * 4 + 4
size_data_per_element_	第0层节点表中，需占多少字节 = size_links_level0_ + data_size_ + 8(存储label，64位cpu)
offsetLevel0_	0。这个子段无实际意义
offsetData_	数据域offset = size_links_level0_
label_offset_	label的offset = size_links_level0_ + data_size_
max_elements_	最大数据量，构建时指定，可以热更新(resizeIndex)
cur_element_count	当前记录数，初始为0
fstdistfunc_	一个快速计算(L2/IP)距离的func
dist_func_param_	维度
maxlevel_	索引当前层数，初始为-1
element_levels_	每个节点在哪一层，是vector数组，数组索引是节点内部id。vector，初始化为max_elements个0
mult_	1 / log(1.0 * M_)，用于计算新增向量落在哪一层。层 = -log(0.0~0.1随机数) / log(M_)，M_越大，层越小。
revSize_	1/mult_ = log(1.0 * M_)
enterpoint_node_	随机进入点的内部id，初始为-1，
link_list_locks_	节点邻居表锁，每个节点一个。vector，初始化为max_elements个std::mutex
cur_element_count_guard_	增员减员锁
global	全局互斥锁，增加新成员时可能上锁
link_list_update_locks_	更新占坑锁，它限定了增量的速度，个数由下面的max_update_element_locks决定。vector，初始化为max_update_element_locks个std::mutex
max_update_element_locks	决定全局同时最多可以有多少个向量在增加，构建时指定，默认65536
level_generator_	随机数发生器，决定新增的向量在哪一层
update_probability_generator_	随机数发生器，增量更新时，概率的让邻居节点更新邻居。实际上不生效。
label_lookup_	label与内部id的映射，unordered_map
data_level0_memory_	节点表，char*，连续数组
linkLists_	节点邻居跳表，char**，每个节点对应数据依然是连续数组
size_links_per_element_	每个节点对应邻居跳表，在每一层需占的空间 = maxM_ * 4 + 4
visited_list_pool_	图操作经常需要判断哪些节点已经走过，这里提供一个已经申请好空间的池子，减少内存频繁申请释放的开销

2、数据结构分析 

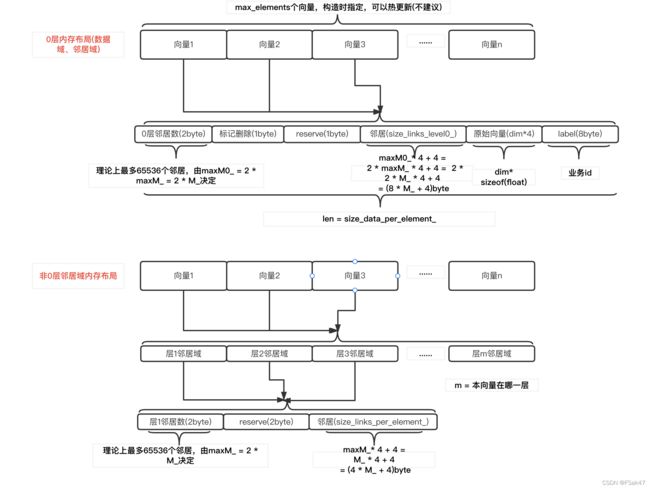
0层内存

        和跳表一样，第0层保存了全部向量数据。包括向量数据域(原始向量、label(向量的业务id))、邻居域(每个向量在第0层的近邻向量id)。

        数据结构如上图：

        首先是header，header前2字节指定该向量在0层当前有几个邻居，后面一字节是标记删除位(增量构建用到)，为内存对齐header第四字节废弃；

        然后是邻居域：这里实际是在构造时就申请好了内存，每个0层向量可以有maxM0_个邻居向量(是非0层的2倍)，占用字节数 = maxM0_ * 4 + 4字节

        最后是数据域：占用字节数 = dim * sizeof(float) = dim * 4字节，以及label，对于我们就是向量id(如feed_id、video_id)，占用8字节，共计dim*4+8字节

        0层全部数据保存在data_level0_memory_，构造索引时通过参数max_elements指定索引最大向量个数，data_level0_memory_一次性申请max_elements * size_data_per_element_字节的内存。目前我们在使用中没有考虑热更新，max_elements均设置为构建索引时数据量。

        提供resizeIndex函数，指定新的最大向量个数max_elements，只是调整0层内存的同时，还要调整节点跳表、节点层映射、遍历回溯池等内存。如考虑热更新，建议构建时设置业务足够大的max_elements，并走增量更新。

非0层内存

        非0层主要存储每个向量在各个层的邻居表。具体是保存了每个向量丛它所在层向低层的邻居。如向量a构建时落在第3层，那么构建过程会不断更新它在1、2、3层的邻居向量。

        linkLists_是邻居表存储实体，是一个二维数组，行由max_elements即最大向量个数指定，列由该向量实际落在的层数，在构建该向量时具体分配内存。

hnsw的本质

图近邻查询最容易想到的思路

        图作为近邻查询最容易被想到的方式就是，距离相近的向量，成为图相邻点，这样查询就可以像一样的查询，但存在如下问题：

        a、当给出一个待查询向量，从图中哪个节点开始查询？

        和faiss-IVF系索引(IVFflat、IVFPQ)等不同，图并没有聚类索引，那么怎么知道从哪查？

        b、为解决问题a，可以比如随机选一个向量作为查询入口，但是每个向量都以和自己非常相近的向量相连(某种意义上就像faiss-IVF系索引的感觉)，与待查询向量距离很远并不相连，那么图是需要很久才能走到待查询向量所在区域的。

        所以需要一种，能够让每个图节点，不仅和近邻相连，还能"有机的"和稍远的节点相连，且还要有效控制相连节点个数，避免查询很慢。

图近邻查询

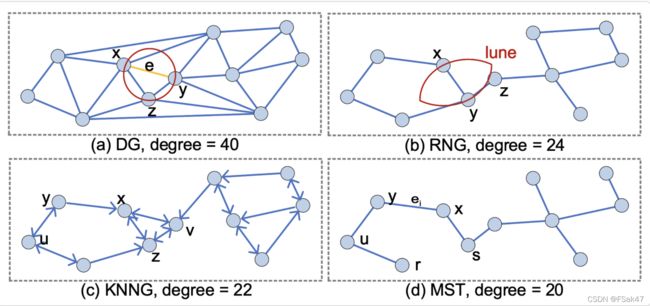
        据调研图近邻查询，脱不出如下b、c、d机制：

        这次分享主要考虑b，不展开c、d。其中c是一些大厂近期取得成功突破的地方，后续将重点研究。

        a是所可以达到召回率=1的理想机制，它能确保从任意一个点出发，都获取完全精确的结果，它的构建思路是：针对每个节点，在构建过程中，不断保证最近邻的k个节点作为邻居相连。这种方式随着数据量增大，节点相连量之大极度严重，即便做一些规则优化也不行(hnsw前身nsw)

        b是hnsw的机制，hnsw主要做了两方面的优化：

        b.1、通过"排除近亲"的机制，增强每个向量与随机的更远向量的相连能力

        所谓"排除近亲"机制，就是当计算新增向量a的邻居向量时，如果待新增的邻居向量b，与已经加入邻居的向量c的距离，小于b与a的距离，那么b不予以加入邻居。

        b.2、如跳表一样，拟合对数分布的数据分层，形成节点由少至多的层次分布，每个向量均在所在及以下层次，维护自己的本层近邻。

        这样，查询入口向量(enterpoint)由最高层的最新加入向量充当，增量构建时，都由enterpoint查到和待处理向量近邻的近邻向量集合，作为待处理向量的潜在邻居，并基于b.1的"排除近亲"机制，选择最合适的邻居，同时最合适的邻居也通过同样机制，重新更新自己的邻居。

        这是hnsw构建索引之所以相对耗时的地方，因为向量更新需要如下操作：

        FOR [待处理向量所在层(或当前最高层), 0层]:

                b.3、一方面，尽可能挖掘潜在的邻居候选集(邻居的邻居的邻居的邻居的邻居......最多ef_construction_个)

                b.4、然后，按"排除近亲"选出最合适作为邻居(M_个)

                b.5、每个新邻居，也要按"排除近亲"重新确认自己的邻居

        不过这些机制确保了，每个向量的邻居，不至于很远很离谱 + 但也不全都是很近 + 同时可以log(总向量个数)的找到目标向量。

        PS：b.3～b.5，是hnsw索引经常被认为无法实现热增量更新的原因，不过在充分调研源码后，个人认为完全可以实现增量热更新。

hnsw数据增删改机制

锁

        hnsw是先天的增量构建，但并非必须一条一条构建，源码配置是最多65536个向量可以并发构建。所以需要一些互斥机制保证索引正常构建，主要包括四类互斥：

增员锁

        cur_element_count_guard_增员锁，当新增向量时，用于更新当前向量总数和映射，临界区很小。

增量构建坑位锁

        link_list_update_locks_增量构建坑位锁，65536个，如果同时占满，下一个向量无法需等待对应坑位释放。贯穿向量的创建/更新的全过程。

节点邻居表更新锁

        link_list_locks_节点邻居表更新锁，每个向量都有一个，用于更新自己的邻居表。由于hnsw的精髓就在于通过向量的新增/更新，不断修正已有邻居向量的邻居以使得更加合理，所以这个锁不仅作用于新增向量本身，而且作用于涉及的邻居节点。

全局锁

        global全局锁，这个锁仅在新增向量流程中，且所在层大于当前最大层时。因为涉及更新maxlevel_及相关向量在最新maxlevel_层的邻居配置，所以该锁会阻塞其他新增向量流程。

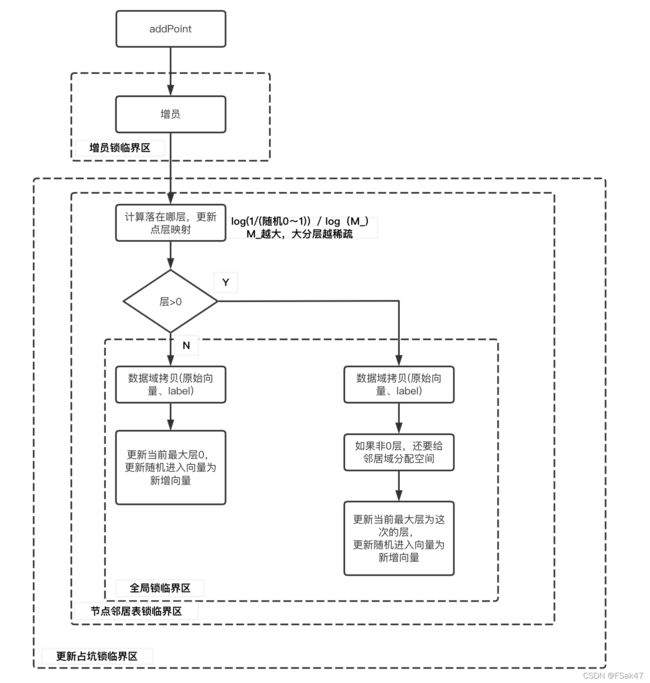
        下面以第一个向量的新增过程，简要感受下四个锁的使用：

索引更新机制

        和传统正倒排索引一样，hnsw没有物理上的向量删除，而是标记删除，标记删除后的向量，在第0层的header中置flag为1，在邻居的更新(由新增/更新向量触发)、查询会产生相应影响。所以重点关注新增向量和更新向量。

新增向量

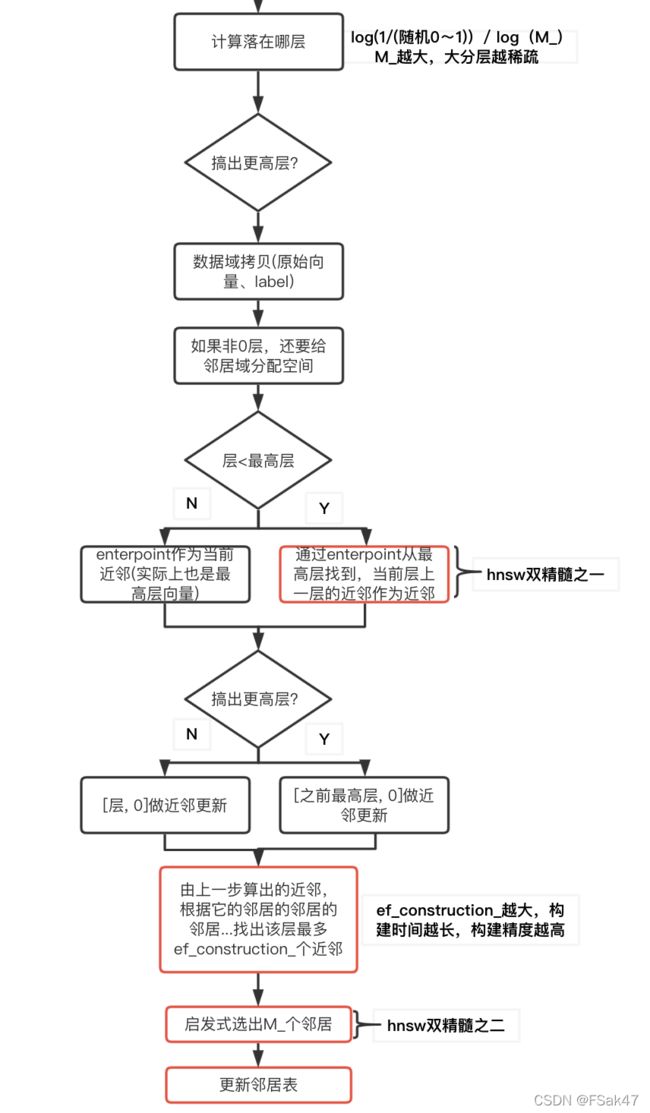
        上图是第一个向量新增的过程，整体非常简单，因为索引是空的，不需要考虑近邻的更新，下面是第2～n个向量新增的过程：

        限于尺寸重要细节没有都画在图中，重要环节中红框中体现。

        第一个红框：

                首先需要弄明白，第一个红框究竟在干什么：它在查找待新增向量，在当前层的最近邻。为什么要找这个？因为要找到当前层，待新增向量，最可能是邻居的潜在邻居集合(也就是第二个红框做的事)，然后再挑出合理的邻居(第三个红框做的事)。

                层次表如何能做到，从最高层的enterpoint向量，很快的找到待新增向量的潜在近邻？首先以enterpoint作为基准向量，它的邻居中，如果存在离待新增向量更近的，那么就以这个邻居作为基准，再以它的邻居继续去找。本层的全都找遍了，进入下一层接着找，这样绝不会找漏或找错，如下伪代码：

最近邻向量 = enterpoint
最近邻距离 = dist(enterpoint，待新增向量)

for 当前最高层 to 待新增向量所在层上一层 {
    bool 找到本层更近邻的 = false
    while(1) {
        邻居集合 = 最近邻向量.当前层邻居
        for (邻居 ： 邻居集合) {
            if (dist(邻居，待新增向量) < 最近邻距离) {
                找到本层更近邻的 = true
                最近邻向量 = 邻居
                最近邻距离 = dist(邻居，待新增向量)
            }
        }

        if (!找到本层更近邻的) {
            break
        }
    }
}

               经实验，索引构建初始时，向量比较少尤其高层向量更少，这一步速度非常快。索引构建后期这步速度也很快，这是hnsw层次化找到目标区域的优点。是hnsw双精髓之一。

         第二个红框：

                上一步找到了待新增向量，在其所在层的当前最近邻向量，这里要做的是，圈出从本层开始到第0层，每一层，待新增向量的潜在邻居。这一步的查找范围也很大，在当前层里，将邻居的邻居的邻居.......，全都过了一遍，伪代码如下：

潜在邻居大顶堆 = {当前层最近邻}
最近邻距离 = 潜在邻居大顶堆.堆顶的dist
while (!潜在邻居大顶堆.empty()) {
    if (潜在邻居大顶堆.size >= ef_construction_) {
        break
    }

    最近邻向量 = 潜在邻居大顶堆.top().pop()
    邻居集合 = 最近邻向量.邻居
    for (邻居 : 邻居集合) {
        if (dist(待新增向量，邻居) < 最近邻距离) {
            潜在邻居大顶堆.push(邻居)
            if (潜在邻居大顶堆 >= ef_construction_) {
                潜在邻居大顶堆.pop()
            }
            最近邻距离 = 潜在邻居大顶堆.堆顶的dist
        }
    }
}

                 经试验，这一步耗时相对占比较多。

        第三个红框：

                上一步选出了最多ef_construction_个潜在邻居，这里要精选出M_个，最终作为待新增向量在本层的邻居。相比NSW的只选最近邻的k个作为邻居，hnsw思路如下伪代码：

最近邻向量 = 候选集.反转小顶堆.堆顶
邻居结果集合 = {}
while (候选集.反转小顶堆) {
    if (邻居结果集合.size == M_) {
        break
    }

    待判定邻居 = 候选集.反转小顶堆.top().pop()
    bool 选择 = true
    dist_to_query = dist(待新增向量, 待判定邻居)
    for (邻居 ：邻居结果集合) {
        if (dist(邻居, 待判定邻居) < dist_to_query) {
            选择 = false
            break
        }
    }

    if (选择) {
        邻居结果集合.push(待判定邻居)
    }
}

                 这一步代码跑的非常快，同时取得了非常好的随机化邻居的能力，是hnsw双精髓之二。

        第四个红框：

                首先给待新增向量，将上一步的之多M_个邻居结果，写入该向量在本层的邻居表。

                同时，针对这些邻居，它们也要重新算它们在本层的邻居，伪代码如下：

for (邻居 ：邻居结果集合) {
    // 这一步在纯新增确实不会发生，但如果是增量更新，就是可能发生的了
    bool exist = 待新增向量是否在邻居中已存在
    if (!exist) {
        邻居表 = 邻居.本层的邻居表
        if (邻居表.full()) {
            邻居集合 = {所有当前邻居, 待新增向量}
            启发式搜索(邻居集合, 邻居表长度)
            更新邻居表
        } else {
            邻居表.append(待新增向量)
        }
    }
}

                这一步速度也很快。

更新向量

        这里具体指的是，曾经被标记删除的向量，又再次被调用addPoint了(前提是label不变)。hnsw针对向量标记删除，虽然在查询时不会召回，但在所有的邻居更新中，都会带上被标记删除的向量一起做更新，这点和传统正倒排索引一样。通过标记删除减轻删除的成本，同时很重要的是，并不会影响向量检索的质量，因为向量本身还在参与近邻的不断更新，仅有的影响是：在查询时会滤去带有删除标记的结果，可能影响返回向量个数。

        除此以外这里的思想、代码逻辑与新增向量，是完全一样的。

查询向量

        查询之所以特别快，除了hnsw双精髓的原因以外，还有hnsw的查询是默认"索引没有增量更新"的前提之下的，也就是向量新增/更新时的各类锁机制，在查询时完全没有加锁的。这也是hnsw支持比较完备的增量更新的障碍之一，不过应该完全可以解决。

        伪代码如下：

最近邻向量 = enterpoint
最近邻距离 = dist(最近邻向量，待查询向量)
for 当前最高层 to 第1层 {
    bool 找到本层更近邻的 = true
    while(1) {
        找到本层更近邻的 = false
        邻居集合 = 最近邻向量.当前层邻居
        for (邻居 ： 邻居集合) {
            if (dist(邻居，待新增向量) < 最近邻距离) {
                找到本层更近邻的 = true
                最近邻向量 = 邻居
                最近邻距离 = dist(邻居，待新增向量)
            }
        }

        if (!找到本层更近邻的) {
            break
        }
    }
}

// 至此找到了直至第1层，待查询向量的最近邻向量，接下来进入第0层找
邻居大顶堆 = {最近邻向量}
最近邻距离 = dist(最近邻向量，待查询向量)
邻居结果集合大顶堆 = {}
while (!邻居大顶堆.empty) {
    if (邻居结果集合大顶堆.size == k) {
        break
    }

    待判定邻居 = 邻居大顶堆.top().pop()
    for (邻居 ：待判定邻居.第0层邻居) {
        if (dist(邻居, 待查询向量) < 最近邻距离) {
            邻居大顶堆.push(邻居)

            if (这个邻居没有标记删除) {
                邻居结果集合大顶堆.push(邻居)
            }
            if (邻居结果集合大顶堆.size > k) {
                邻居结果集合大顶堆.pop()
            }
            最近邻距离 = 邻居结果集合大顶堆.top().dist()
        }
    }
}

hnsw源码分析

        faiss和hnsw源码分析实际上已完成，后续将结合增量更新等实践，性能优化手段调研，一起分享出来。

总结

        1、hnsw源码在第0层的邻居的确定，依然通过启发式即"排除近亲"的方式选择，而第0层个人认为已经不需要这样去做，这方面将做一些实验去验证；

        2、hnsw索引绝对可以保证高的召回率，相对faiss-ivf系索引，在同等近乎100%召回率结果下，hnsw的耗时几乎是ivf-flat的10倍(平均、p99)，作为ivf-flat的优化，ivfpq及其变种虽然可以减少耗时，但召回率有下降(因为引入了更多的量化)。所以基本上可以说，基于图的比较优秀的算法如hnsw(及一些演进品)，应作为后续我们索引的选择，feed的索引应尽快调整过来。

        3、hnsw的索引已经存储了原始向量，且可以获取(经充分调研faiss源码，faiss-ivf系索引，也可以获取原始向量)，当前的相似度debug工具，应尽快去掉"id_emb_mapping"文件的构建上传和加载。

        4、索引分片不应该是hnsw要考虑的问题

        根据hnsw的特点，hnsw确实不易于索引分片，而且鉴于其性能也不应该考虑去做分片，那样只能反而更糟。根据大量文章调研，部分大厂针对数十亿量级的数据，可以做到用类似hnsw的算法，8核+64G内存的单机，就能实现很高的查询性能，结合我们当前的数据量，数据量很长一段时间内，不会是我们的瓶颈。

        5、hnsw我们可以考虑研发增量热更新

        hnsw的增量更新，不论是新增向量还是更新向量，涉及更新许多向量且是多层邻居表，而查询时完全没有加锁行为(所以它是默认无热更新)，这是实现热更新的阻碍。

        考虑传统正倒排索引的业界优秀解决方案：如大规模广告系统的索引，在高负载情况下的更新方式其实是：增量构建小索引一同提供查询 + 小索引定容/定时merge合入大索引，这是在大促高流量场景下已验证的成熟方案，hnsw的增量更新面对的问题实际上是一样的，完全可以解决。这将是我们的一大亮点。

        PS：经源码调研，faiss-ivf系索引(ivf-flat、ivfpq系列)同样完全可以实现增量，某公司的开源，即是对IVFPQ做了(相对粗糙的)的增量工程化