【机器学习】梯度下降算法原理和实现
梯度下降是许多机器学习模型中都会直接或间接使用的算法。
什么是梯度
以二元函数![]() 为例,假设其中每个变量都具有连续的一阶偏导数
为例,假设其中每个变量都具有连续的一阶偏导数![]() 和
和 ![]() ,则这两个偏导数构成向量:
,则这两个偏导数构成向量:![]() ,即为该二元函数的梯度向量,一般记作
,即为该二元函数的梯度向量,一般记作![]() 。根据这个概念,可以看看多元函数求梯度的例子。
。根据这个概念,可以看看多元函数求梯度的例子。
![]()
在一元函数中,梯度是微分,是函数的变化率,在多元函数中,梯度变成了向量,同样表示函数的变化方向。从几何意义来讲,梯度的方向表示的是函数增加最快的方向,这正是我们下山要找的“最陡峭的方向”的反方向!因此后面要讲到的迭代公式中,梯度前面的符号为“-”,代表梯度方向的反方向。在多元函数中,梯度向量的模(一般指二模)表示函数变化率,同样的,模数值越大,变化率越快。
梯度下降的目的
绝大多数的机器学习模型都有一个损失函数。
比如常见的均方误差(Mean Squared Error)损失函数:
其中,![]() 表示样本数据的实际目标值,
表示样本数据的实际目标值,![]() 表示预测函数
表示预测函数![]() 根据样本数据
根据样本数据![]() 计算出的预测值。
计算出的预测值。
损失函数是用来衡量机器学习模型的精确度的。一般来说,损失函数的值越小,模型的精确度就越高。提高机器学习模型的精确度,需要尽可能降低损失函数的值,而降低损失函数的值,一般采用梯度下降方法。
梯度下降的目的,为了最小化损失函数。
梯度下降的原理
第一步:需要寻找损失函数的最低点(前进方向),在这里,使用微积分里的导数,通过求出函数导数的值,从而找出函数下降的方向或者是最低点。
损失函数里一般有两种参数,一种是控制输入信号量的权重(Weight, 简称![]() ),另一种是调整函数与真实值距离的偏差(Bias,简称
),另一种是调整函数与真实值距离的偏差(Bias,简称![]() )。我们所要做的工作,就是通过梯度下降方法,不断地调整权重
)。我们所要做的工作,就是通过梯度下降方法,不断地调整权重 ![]() 和偏差
和偏差![]() ,使得损失函数的值变得越来越小。
,使得损失函数的值变得越来越小。
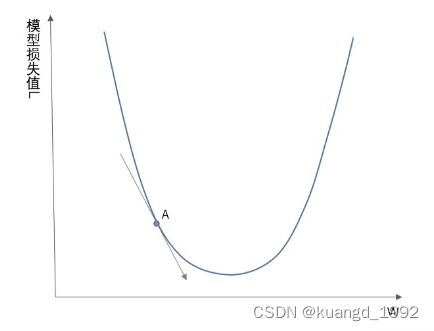
假设某个损失函数中,模型损失值![]() 与权重
与权重![]() 是下图中的关系。
是下图中的关系。
上图中,权重![]() 目前的位置是在A点,此时求出A点的梯度:
目前的位置是在A点,此时求出A点的梯度:![]() ,便能知道需要向右移动,可以是损失函数的值变得更小。
,便能知道需要向右移动,可以是损失函数的值变得更小。
通过上面的简单示例可以知道,通过计算梯度,可以知道权重![]() 的移动方向。
的移动方向。
上述例子中,只出现了一个权重![]() ,实际上项目中样本数据会有很多个。对于每一个样本数据,都可以求出一个权重的梯度。这时,需要把各个样本数据的权重梯度加起来,求出平均值,用平均值来作为样本整体的权重梯度。
,实际上项目中样本数据会有很多个。对于每一个样本数据,都可以求出一个权重的梯度。这时,需要把各个样本数据的权重梯度加起来,求出平均值,用平均值来作为样本整体的权重梯度。
第二步:确定应该前进多少
通过计算梯度,知道了权重的移动方向。那么,需要移动多少呢?
这里要用到学习率(Learning Rate)。通过学习率,可以计算前进的步长。
用![]() 表示权重初始值,
表示权重初始值,![]() 表示更新后的权重值,用
表示更新后的权重值,用![]() 表示学习率,则有:
表示学习率,则有:
在梯度下降中,会重复上面公式多次,直到损失函数值收敛不变。
如果学习率 ![]() 设置得过大,有可能我们会错过损失函数的最小值;如果设置得过小,可能我们要迭代式子(2)非常多次才能找到最小值,会耗费较多的时间。因此,在实际应用中,我们需要为学习率
设置得过大,有可能我们会错过损失函数的最小值;如果设置得过小,可能我们要迭代式子(2)非常多次才能找到最小值,会耗费较多的时间。因此,在实际应用中,我们需要为学习率 ![]() 设置一个合适的值。
设置一个合适的值。
对于偏差![]() 的优化过程,和上面的过程相同。
的优化过程,和上面的过程相同。
梯度下降法的一般求解框架
1、给定待优化连续可微函数
、学习率
以及一组初始值
2、计算待优化函数梯度:
3、更新迭代公式:
4、计算
处函数梯度
5、计算梯度向量的模来判断算法是否收敛:
6、若收敛,算法停止,否则根据迭代公式继续迭代
梯度下降的过程
1.for i = 0 to 训练数据的个数:
(1) 计算第 i 个训练数据的权重 w 和偏差 b 相对于损失函数的梯度。于是我们最终会得到每一个训练数据的权重和偏差的梯度值。
(2) 计算所有训练数据权重 w 的梯度的总和。
(3) 计算所有训练数据偏差 b 的梯度的总和。
2. 做完上面的计算之后,我们开始执行下面的计算:
(1) 使用上面第(2)、(3)步所得到的结果,计算所有样本的权重和偏差的梯度的平均值。
(2) 使用下面的式子,更新每个样本的权重值和偏差值。
重复上面的过程,直至损失函数收敛不变。
伪代码如下:
def train(X, y, W, B, alpha, max_iters):
'‘’
选取所有的数据作为训练样本来执行梯度下降
X : 训练数据集
y : 训练数据集所对应的目标值
W : 权重向量
B : 偏差变量
alpha : 学习速率
max_iters : 梯度下降过程最大的迭代次数
'''
dW = 0 # 初始化权重向量的梯度累加器
dB = 0 # 初始化偏差向量的梯度累加器
m = X.shape[0] # 训练数据的数量
# 开始梯度下降的迭代
for i in range(max_iters):
dW = 0 # 重新设置权重向量的梯度累加器
dB = 0 # 重新设置偏差向量的梯度累加器
# 对所有的训练数据进行遍历
for j in range(m):
# 1. 遍历所有的训练数据
# 2. 计算每个训练数据的权重向量梯度w_grad和偏差向量梯度b_grad
# 3. 把w_grad和b_grad的值分别累加到dW和dB两个累加器里
W = W - alpha * (dW / m) # 更新权重的值
B = B - alpha * (dB / m) # 更新偏差的值
return W, B # 返回更新后的权重和偏差。其他常见的梯度下降算法
上面介绍的梯度下降算法里,在迭代每一次梯度下降的过程中,都对所有样本数据的梯度进行计算。虽然最终得到的梯度下降的方向较为准确,但是运算会耗费过长的时间。于是人们在上面这个算法的基础上对样本梯度的运算过程进行了改进,得到了下面这两种也较为常见的算法:
1. 小批量样本梯度下降(Mini Batch GD)
这个算法在每次梯度下降的过程中,只选取一部分的样本数据进行计算梯度,比如整体样本1/100的数据。在数据量较大的项目中,可以明显地减少梯度计算的时间。
2. 随机梯度下降(Stochastic GD)
随机梯度下降算法只随机抽取一个样本进行梯度计算,由于每次梯度下降迭代只计算一个样本的梯度,因此运算时间比小批量样本梯度下降算法还要少很多,但由于训练的数据量太小(只有一个),因此下降路径很容易受到训练数据自身噪音的影响,看起来就像醉汉走路一样,变得歪歪斜斜的。
参考文档:https://www.jianshu.com/p/424b7b70df7b