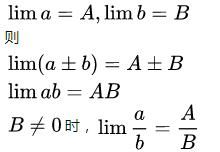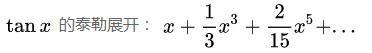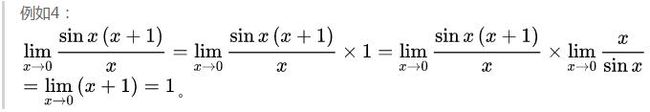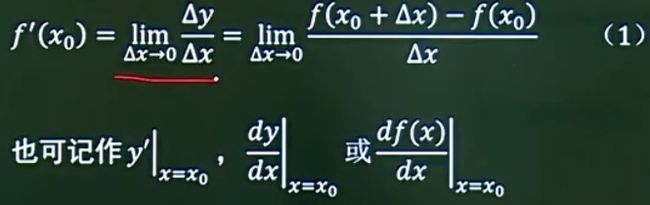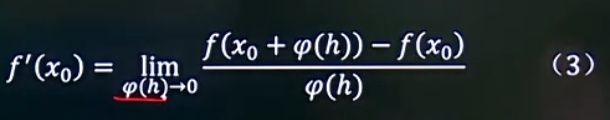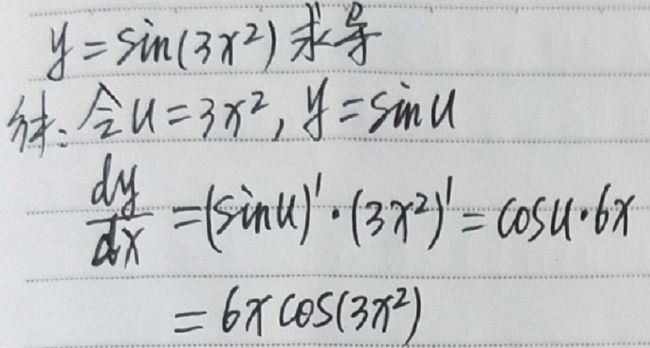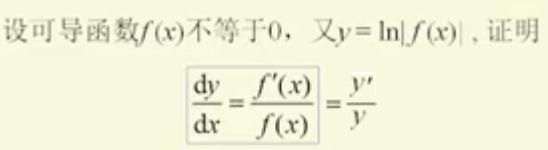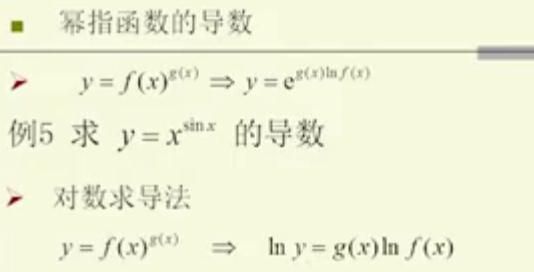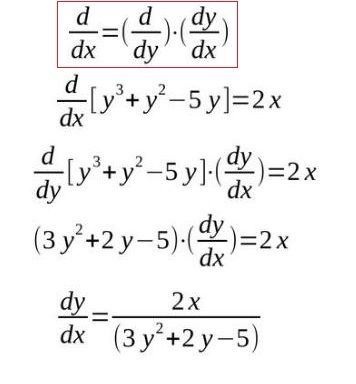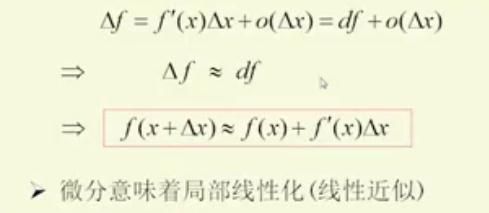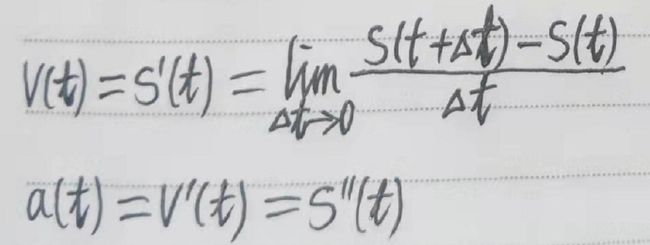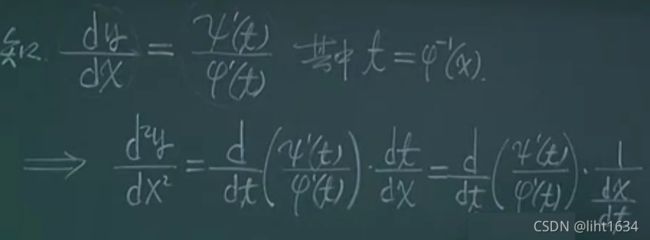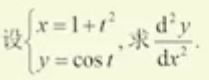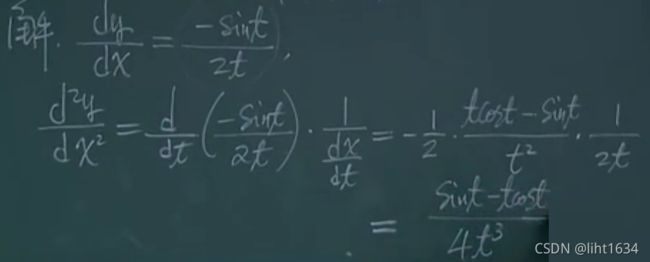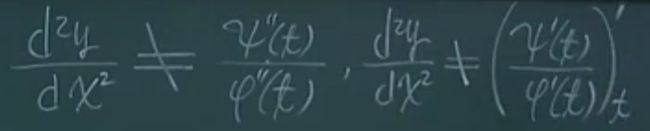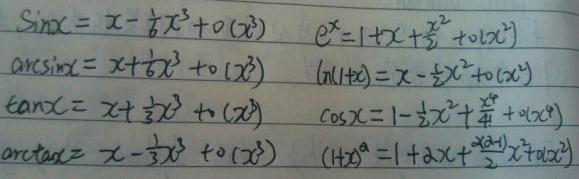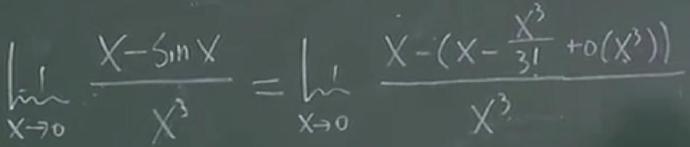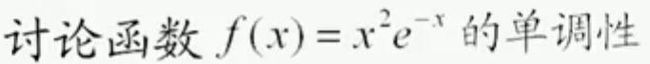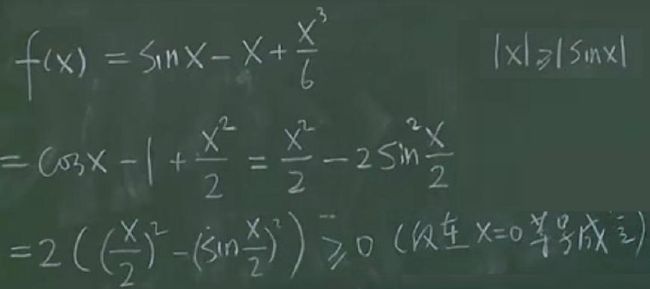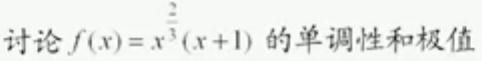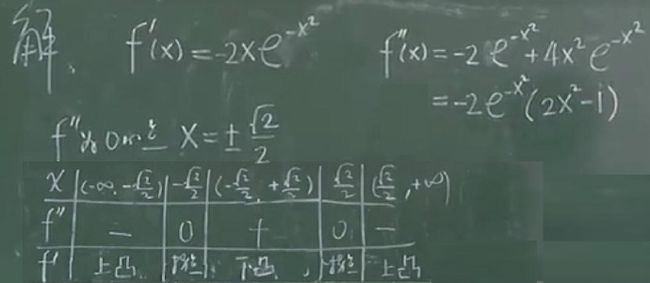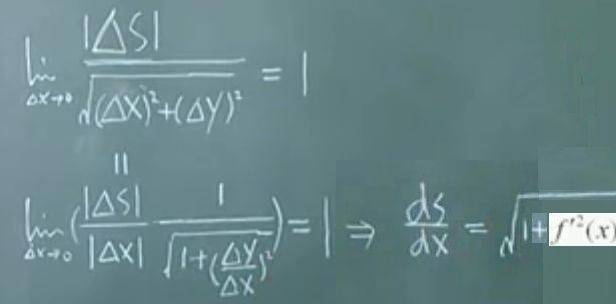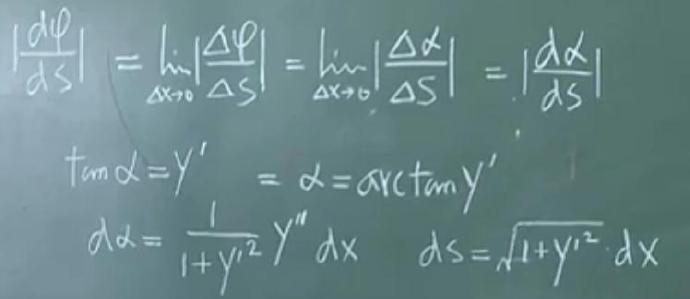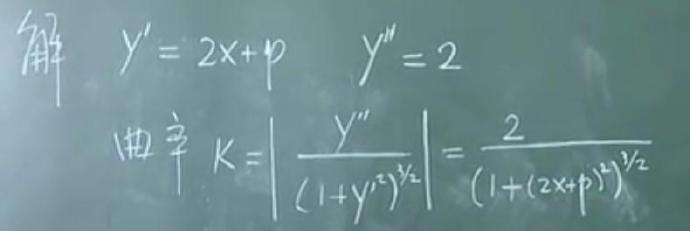微积分基础1-微分篇

目录：

一、预备知识

1、极限的定义

1）数列的极限   2）函数的极限

2、邻域

1）为什么函数极限的定义要求邻域去心   2）为什么函数连续的定义不要求邻域去心

3、等价无穷小替换

4、间断点

二、微分

1、导数的定义

2、导函数

1）基本初等函数求导公式   2）函数的和、差、积、商的求导法则  3）复合函数求导

4）反函数的求导法则   5）隐函数求导   6）极座标方程表示的函数的导数

7）导数的应用

3、可导与连续

4、微分的概念

1）微分定义   2）可微与可导的关系   3）几何意义   4）近似计算   5）复合函数的微分

5、高阶导数

1）高阶导数的概念   2）隐函数的二阶导数   3）参数方程确定的函数的二阶导数

4）高阶导数求法   5）高阶导数公式

6、微分中值定理与导数的应用

1）费马、罗尔、拉格朗日定理   2）柯西定理

7、洛必达法则

8、泰勒Taylor公式及其应用

1）一点附近的泰勒公式    2）区间(a,b)上的泰勒公式   3）常用泰勒公式

9、利用导数研究函数性态

1）函数的单调性与极值   2）极值判别法   3）最值的求法   4）函数凹凸性与拐点

5）二阶导数的意义总结   6）函数的作图(借助图解数学)

10、平面曲线的曲率

1）弧长与弧微分   2）曲率

11、方程的近似解

-----------------------------------------------------------

‘无限细分’就是微分，‘无限求和’就是积分。无限就是极限，极限的思想是微积分的基础，它是用一种运动的思想看待问题。比如，子弹飞出枪膛的瞬间速度就是微分的概念，子弹每个瞬间所飞行的路程之和就是积分的概念。你也能懂的微积分

-----------------------------------------------------------------------------------------------------------------

一、预备知识

1、极限的定义

1）数列的极限

任给ε>0，就是一个任意小的正数，总是存在N，这个N是指第N项，不管这个N有多大，只要n一超过N就有后面的不等式成立。

两个数作差的绝对值也就是两个数之间的距离，这个距离要小于任意小的一个数ε，意思就是这两个无限接近，这就说清了当n趋向于无穷大时，这个数列的值是无限接近于A。

n>N指这个数列不一定每一项都是趋向于这个数A，但是必须在数列的某一项后面的所有项都趋向于这个数。

图1.1.1

--------------------------------

2）函数的极限

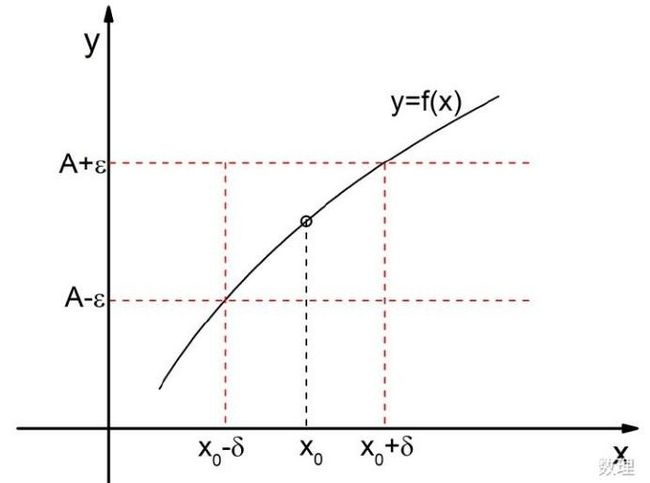
（1）极限定义

图1.1.2

 

举例：

 对于连续函数f(x)，f(x)在A以及A的邻域有定义，有。

关于连续：设函数f(x)在点x0的某个邻域内有定义,若 lim(x→x0)f(x)=f(x0), 则称f(x)在点x0处连续。 若函数f(x)在区间I的每一点都连续,则称f(x)在区间I上连续。

主要运用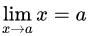，以及前面这些性质。那么这个过程必须要这么做：

（1）极限表达式本身是个连续函数（对于大部分初等表达式都满足条件）

（2）不拆分成四则运算的时候，对整个极限表达式中求极限的变量，要么全都“代入”，要么不代入，不能只代入一部分。这是因为本质上是求连续函数在极限点的值。比如说对于nexp(f(n))这样的，不能只在指数中代入n，外面保留，会出问题。

（3）函数必须满足在该点有定义，比如说如果分母求值是0，那么这一点就没有定义了；再比如对数里面是0，tan里面是π/2之类。

（4）拆成四则运算的时候，一般来说是将极限拆成了两个独立的部分，必须保证这两部分各自的极限都是存在的，尤其是乘除法的时候。对于除法，还要保证分母部分的极限不为0。

比如说你这个过程当中，

（1）是首先把极限拆成了极限的和，而且两部分极限都仍然存在，这样第二部分就直接可以用连续函数代入；

（2）是把极限拆成了极限的乘积，两部分极限都仍然存在，所以是正确的；

（3）直接代入不行是因为分子分母都是0，没有定义，所以变形到分母不为0的形式，就可以代入了。

-----------------

（2）两个重要极限

图1.1.3

-----------------------------------------------------------

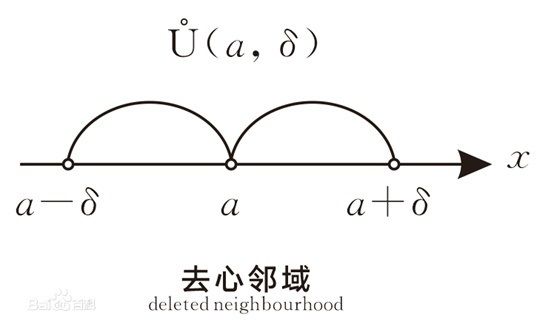
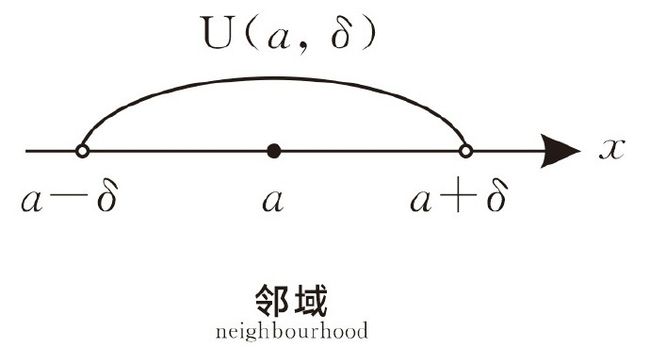
2、邻域

图1.2.1

图1.2.2

以a为中心的邻域是用来刻画与a接近的程度，那么以a为中心的去心邻域刻画的是什么呢？是与a接近的【趋势】。

如何理解这个概念？又如何区分这两者对应的数学定义呢？

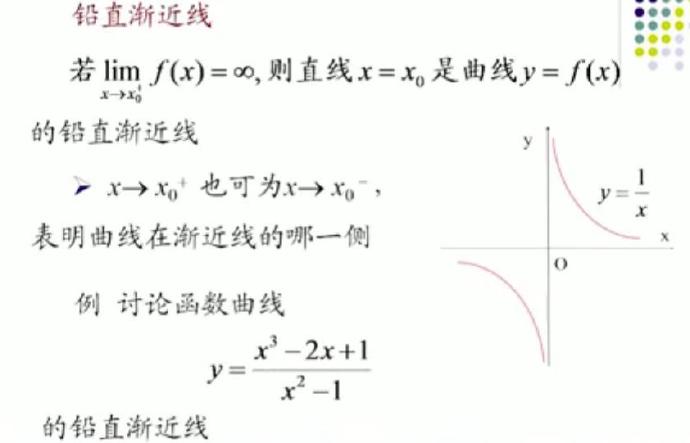
1）为什么函数极限的定义要求邻域去心

在描述x→x0这个趋近的过程时，描述的就是 x→x0表示的就是由x向x0无限接近的过程，但这个过程中我们有x≠x0。

为了体现x→x0但不相等的这个过程，将函数极限的定义取作去心邻域，让x无法取得x0的值。

如此一来，函数极限的定义就变得更为广泛，即使f(x)在x0处没有意义也可以求极限。也就是说，函数在x0处的极限只和函数在该点附近有关，与函数在该点是否有定义可以没有关系。

由此，我们建立了函数极限的定义，于此衍生出来的局部有界性、局部保序性、夹逼定理也自然都是在去心邻域内建立的了。

--------------------------------

2）为什么函数连续的定义不要求邻域去心

在上面的分析中我们知道，函数在x0处的极限只和函数在该点附近有关，与函数在该点是否有定义可以没有关系。

因此，在一段函数图像上，点x处的邻域就可以被拆分成点x与点x的去心邻域两个部分。于是我们很自然地就得到了，要使得一段函数图像连续，那么点x处就必须与它对应的去心邻域结合成一个整体。

上面的分析中，我们知道去心邻域对应的就是点x处的极限值，而点x处对应的就是函数值，如此一来，要将他们联系成一个整体，

只需要让函数值等于极限值即可。

由此，我们建立了函数连续的定义，自然就可以使用连成一个整体的【邻域】，以此类推，可导概念的建立也自然就是使用【邻域】。

-----------------------------------------------------------

3、等价无穷小替换

图1.3.1

-----------------

（1）被替换的量无穷小（取极限时值为0）

-----------------

（2）被替换的量，必须是作为被乘或被除的元素，不能是被加减的元素。

        必须处于因子位置。

无穷小量的等价，不过取了泰勒展开式的第一项去等价罢了。等价无穷小量就是精度较低的泰勒展开。

所以加减可能会导致项的抵消，抵消后，根据分母的阶数可能会需要泰勒展开第一项后的高阶近似，但因为等价无穷小量只取了泰勒展开的第一项，对后续的近似无能为力。

以例3说明，当sinx的一阶代表元（也就是它的等价无穷小量）与tanx的一阶代表元消掉以后，按理说该二阶代表元站出来了，但因为等价无穷小量只取了泰勒展开的第一项，消掉等于0。但我们知道在取完第一项之后后面的项还是有用（根据分母是x的几阶无穷小量）。

-----------------

（3）替换时必须整体替换，而不能替换局部

整体替换是什么意思呢？其实等价无穷小量的替换，我们可以看做是原极限乘以一个极限为1的分式。

整体替换，就是要对整个求极限的式子乘1。

-----------------------------------------------------------

4、间断点

图1.4.1

图1.4.2

-----------------------------------------------------------------------------------------------------------------

二、微分

1、导数的定义

 

利用x - x0 = Δx变形得到

一般地，导数的定义式，还可以写成以下形式(导数的广义定义式)：使用Ψ(h)代替Δx

 

单侧导数：

右导数

左导数

左、右导数统称为单侧导数。

-----------------------------------------------------------

2、导函数

若函数y=f（x）在开区间内每一点都可导，就称函数f（x）在区间内可导。这时函数y=f（x）对于区间内的每一个确定的x值，都对应着一个确定的导数值，这就构成一个新的函数，称这个函数为原来函数y=f（x）的导函数，记作y'、f'（x）、dy/dx或df（x）/dx，简称导数。

--------------------------------

1）基本初等函数求导公式

图2.2.1

解(2)式：

图2.2.2

记忆：这里令n=2，nx^(n-1)=2x^(2-1)=2x。

解(3)式：

图2.2.3

解(9)式：

图2.2.4

--------------------------------

2）函数的和、差、积、商的求导法则

图2.2.5

--------------------------------

3）复合函数求导

图2.2.6

图2.2.7

图2.2.8

图2.2.9

--------------------------------

4）反函数的求导法则

图2.2.10

--------------------------------

5）隐函数求导

图2.2.11

图2.2.12

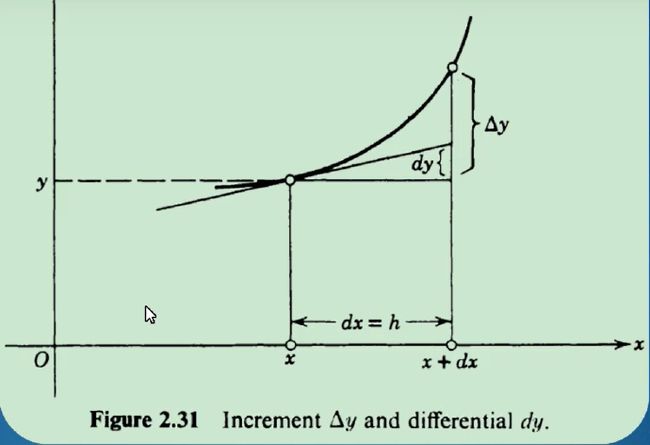
（1）dx是Δx的近似值，其中Δx比dx多了一个高阶无穷小，即：Δx=dx+o(dx) (如图2.4.3所示), 其中o(dx)是比dx高阶的无穷小，这一项非常小故可以忽略，dx ≈ Δx；

（2）如果此处的x是自变量，那么dx = x，通常把自变量x的增量x称为自变量的微分，记作dx；如果这里的x是因变量，那么把自变量写作y的话，x是变化量，dx = 导数*y；

（3）dx是x的微分，Δx是x的改变量。一般两者不等，前者是后者的线性主部(如图2.4.1所述)。但对自变量而言，因为x对x的导数恒等于1，两者相等。反之，两者相等的也只有自变量。或者说，x^n的导数为n*x^(n-1)，那么x的导数就是1。

-----------------

例2 

 

图2.2.13

 

图2.2.14

d是微分符号，dx是x的微分；

d/dy是某函数对y的微分，dy/dx是函数y对x的微分。

--------------------------------

6）极座标方程表示的函数的导数

图2.2.15

--------------------------------

７）导数的应用

（１）变化率

 

-----------------------------------------------------------

3、可导与连续

​

图2.3.1

-----------------------------------------------------------

4、微分的概念
1）微分定义

图2.4.1

--------------------------------

2）可微与可导的关系

​

图2.4.2

函数在 x 处的导数为 f'(x)，在 x 处的微分为 f'(x)dx。比如d(cosx) = (cosx)'dx = -sinx dx。

--------------------------------

3）几何意义

斜率是过某一点的直线倾斜程度，而导数是函数，也可以说，导数是原函数曲线上每一个点处切线斜率的集合，可能是常数，也可能是函数式。

导数的几何意义就是曲线上某点的斜率,一点横坐标代入导函数中所得的值是该点的切线的斜率值。某点的导数等于该点切线的斜率。

图2.4.3

Δy = dy + o(dy)

半径为r的圆的面积公式是S=πr²。如果我们让半径增加Δr，那么新的圆面积就应该写成π(r+Δr)²，那么，增加的面积ΔS就应该等于两个圆的面积之差：

这个式子就跟上面的Δy=A·Δx+o(Δx)一模一样。只不过把x和y换成了r和S，A在这里就是2πr，这里的π(Δr)是关于Δr的平方项，这不就是所谓的高阶(平方是2阶，Δr是1阶，2比1更高阶)无穷小o(Δx)么？所以，它的微分ds就是2πr·Δr这一项：

它的几何意义也很清楚：这就是一个长为2πr(这刚好是圆的周长)，宽为Δr的矩形的面积，好像是把这个圆“拉直”了所得的矩形的面积。

--------------------------------

4）近似计算

​

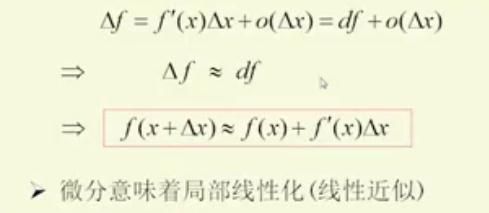
图2.4.4

--------------------------------

5）复合函数的微分

​

图2.4.5

​

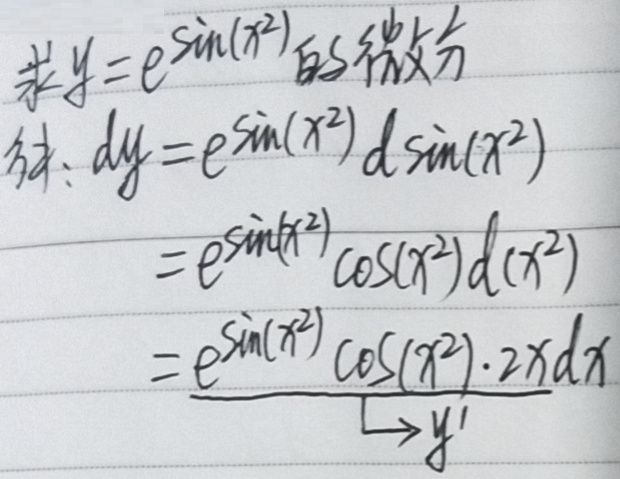
图2.4.6

-----------------------------------------------------------

5、高阶导数

1）高阶导数的概念

​

图2.5.1

​

图2.5.2

位移对时间的二阶导数就是加速度。

​

图2.5.3 

--------------------------------

2）隐函数的二阶导数

​

图2.5.4

--------------------------------

3）参数方程确定的函数的二阶导数

  

--------------------------------

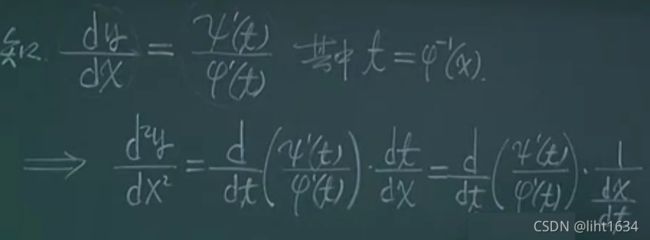
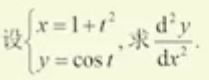
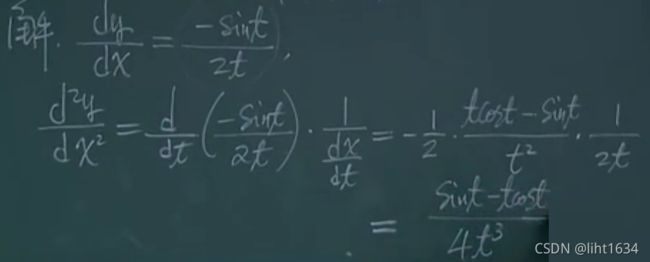
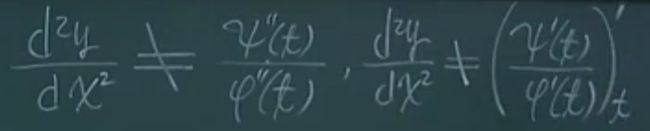
4）高阶导数求法

（1）递归法

 

--------------------------------

5）高阶导数公式

-----------------------------------------------------------

6、微分中值定理与导数的应用

1）费马、罗尔、拉格朗日定理

举例：

--------------------------------

2）柯西定理

​

​

-----------------------------------------------------------

7、洛必达法则

 

举例：

 

-----------------------------------------------------------

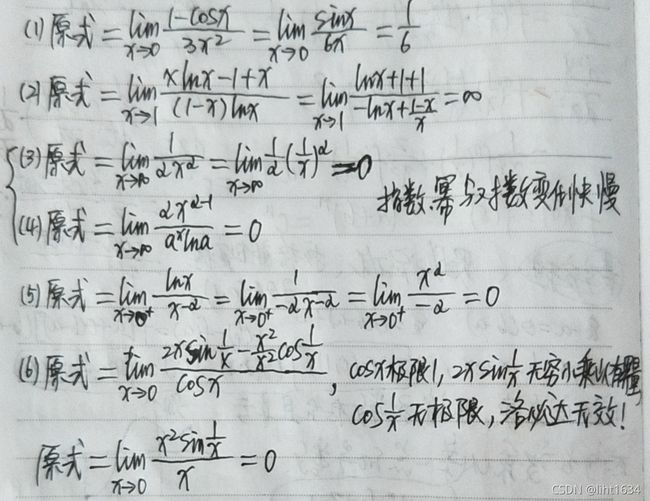
8、泰勒Taylor公式及其应用

前面的内容主要讲解用线性函数近似一个复杂函数，用一条直线近似曲线、一次函数近似复杂函数，这些比较粗糙。

泰勒展开式就是把一个三角函数或者指数函数或者其他比较难缠的函数用多项式替换掉。也就是说，有一个原函数 [公式]，再造一个图像与原函数图像相似的多项式函数 [公式] ,为了保证相似，只需要保证这俩函数在某一点的初始值相等，1阶导数相等，2阶导数相等，……n阶导数相等。怎样更好地理解并记忆泰勒展开式？

 

1）一点附近的泰勒公式

 

 

--------------------------------

2）区间(a,b)上的泰勒公式

举例：

--------------------------------

3）常用泰勒公式

常用泰勒公式近似：

举例：

一个函数只要有任意阶导数，就可以写出它的泰勒级数。泰勒级数若与这个函数相等，那么其余项趋向于0。

-----------------------------------------------------------

9、利用导数研究函数性态

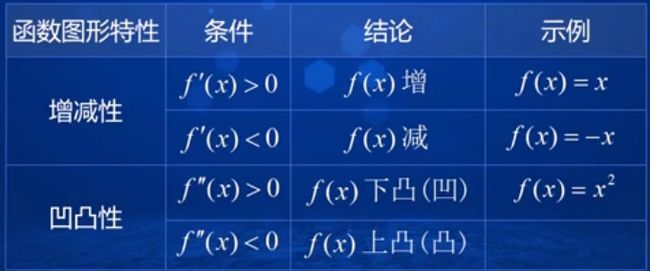
通过简单函数记忆函数图形特性，如下图所示。

1）函数的单调性与极值

举例：

将不等式转换为讨论函数单调性。

--------------------------------

2）极值判别法

（1）极值第一判别法

举例：

-----------------

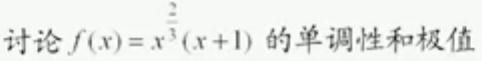
（2）极值的第二判别法

记忆方法：y=x^2二阶导数2>0取得最小值。

--------------------------------

3）最值的求法

前面了解了函数的性态与极值，极值是小范围的最值。

--------------------------------

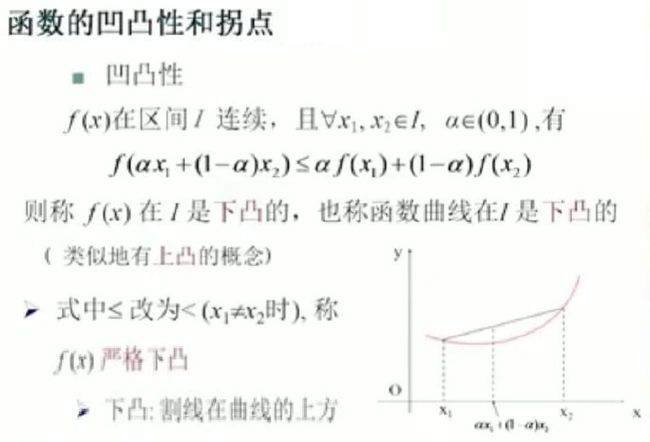
4）函数凹凸性与拐点

（1）函数的凹凸性

记忆方法：y=x^2的两阶导数2>0下凸！
-----------------

（2）拐点

--------------------------------

5）二阶导数的意义总结

二阶导数是对一阶导数再求导一次，意义如下：

（1）斜线斜率变化的速度，表示一阶导数的变化率（如物理上的加速度等）

（2）函数的凹凸性

（3）判断极大值极小值

--------------------------------

6）函数的作图(借助图解数学)

-----------------------------------------------------------

10、平面曲线的曲率

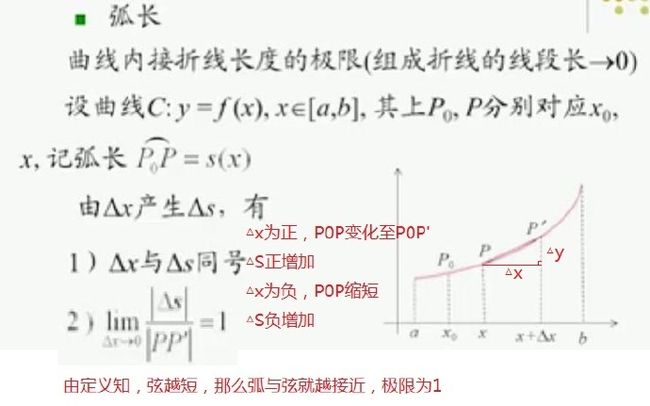
1）弧长与弧微分

--------------------------------
2）曲率

-----------------------------------------------------------

11、方程的近似解

-----------------------------------------------------------------------------------------------------------------