动手学习深度学习 02:预备知识
文章目录
- 01 数据操作 + 数据预处理
-
- 1、数据操作
-
- 1.1、创建数组
- 1.2、访问元素
- 2、数据操作_Code
-
- 2.1、张量
- 2.2、算术运算符
- 2.3、广播机制
- 2.4、索引和切片
- 2.5、节省内存
- 2.6、转换为其他Python对象
- 3、数据预处理
-
- 3.1、读取数据
- 3.2、除去缺失值
- 3.3、转换为张量格式
- 02 线性代数
-
- 1、标量
- 2、向量
-
- 2.1、长度、维度和形状
- 3、矩阵
-
- 3.1、张量
- 3.2、张量算法的基本性质
- 4、线性代数QA
- 5、小结
- 03 微积分
- 04 自动微分
- 05 概率
- 06 查阅文档
01 数据操作 + 数据预处理
1、数据操作
n维数组,也称为张量(tensor),是机器学习和神经网络的主要数据结构
1.1、创建数组
1.2、访问元素
2、数据操作_Code
代码位置: chapter_preliminaries/ndarray.ipynb
- 深度学习存储和操作数据的主要接口是张量(n维数组)。它提供了各种功能,包括基本数学运算、广播、索引、切片、内存节省和转换其他Python对象。
2.1、张量
张量表示由一个数值组成的数组,这个数组可能有多个维度。
- 具有一个轴的张量对应数学上的向量(vector);
- 具有两个轴的张量对应数学上的矩阵(matrix);
- 具有两个轴以上的张量没有特殊的数学名称。
import torch
x = torch.arange(12)
# tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
1、shape :
通过张量的shape属性来访问张量(沿每个轴的长度)的形状
import torch
x = torch.arange(12) # tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
print(x.shape) # torch.Size([12])
2、numel
张量中元素的总数,即形状的所有元素乘积,可以检查它的大小(size)
import torch
x = torch.arange(12) # tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
print(x.shape) # torch.Size([12])
print(x.numel()) # 12
3、reshape
改变一个张量的形状而不改变元素数量和元素值,可以调用reshape函数
import torch
x = torch.arange(12) # tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
print(x.shape) # torch.Size([12])
print(x.numel()) # 12
x = x.reshape(4, 3)
"""
tensor([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
"""
4、zeros
使用全0、全1、其他常量,或者从特定分布中随机采样的数字来初始化矩阵
(1)创建一个形状为(2,3,4)的张量,其中所有元素都设置为0
y = torch.zeros((2, 3, 4))
结果展示:
tensor([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]])
(2)创建一个形状为(2,3,4)的张量,其中所有元素都设置为1
z = torch.ones((2, 3, 4))
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
(3)通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值
n = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(n)
print(n.shape)
print(n.numel())
结果展示:
tensor([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])
torch.Size([3, 4])
12
(4)通过从某个特定的概率分布中随机采样来得到张量中每个元素的值
m = torch.randn(4, 3)
结果展示:
tensor([[ 1.1251, 0.6748, -0.3697],
[ 0.7118, 1.1822, 1.3140],
[-1.1234, 0.8773, 0.2002],
[-0.0407, 0.3170, 0.6610]])
2.2、算术运算符
1、对于任意具有相同形状的张量, 常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。
import torch
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(x + y, x - y, x * y, x / y, x ** y) # **运算符是求幂运算
结果展示:
tensor([ 3., 4., 6., 10.])
tensor([-1., 0., 2., 6.])
tensor([ 2., 4., 8., 16.])
tensor([0.5000, 1.0000, 2.0000, 4.0000])
tensor([ 1., 4., 16., 64.])
2、“按元素”方式可以应用更多的计算,包括像求幂这样的一元运算符。
- torch.exp(x)
import torch
x = torch.tensor([1.0, 2, 4, 8])
print(torch.exp(x))
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
3、除了按元素计算外,我们还可以执行线性代数运算,包括向量点积和矩阵乘法。
- cat : 可以把多个张量连结(concatenate)在一起
我们只需要提供张量列表,并给出沿哪个轴连结。
如:
下面的例子分别演示了,当我们
- 沿行(轴-0,形状的第一个元素)
- 按列(轴-1,形状的第二个元素)
连结两个矩阵
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X1 = torch.cat((X, Y), dim=0) # dim=0 : 按行
Y1 = torch.cat((X, Y), dim=1) # dim=1 : 按列
print("X:", X)
print("Y:", Y)
print("X1:", X1)
print("Y1:", Y1)
结果展示:
一个输出张量的轴-0长度(6)是两个输入张量轴-0长度的总和(3+3);
第二个输出张量的轴-1长度(8)是两个输入张量轴-1长度的总和(4+4)。
X: tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
Y: tensor([[2., 1., 4., 3.],
[1., 2., 3., 4.],
[4., 3., 2., 1.]])
X1: tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]])
Y1: tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]])
4、我们想通过逻辑运算符构建二元张量。 以X == Y为例
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X == Y)
结果展示:
tensor([[False, True, False, True],
[False, False, False, False],
[False, False, False, False]])
5、对张量中的所有元素进行求和,会产生一个单元素张量。
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
print(X.sum())
tensor(66.)
2.3、广播机制
在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作。
这种机制的工作方式如下:
- 首先,通过适当复制元素来扩展一个或两个数组, 以便在转换之后,两个张量具有相同的形状。
- 其次,对生成的数组执行按元素操作。
# a和b分别是和矩阵
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
print(a)
print(b)
print(a + b)
结果展示:
tensor([[0],
[1],
[2]])
tensor([[0, 1]])
tensor([[0, 1],
[1, 2],
[2, 3]])
2.4、索引和切片
就像在任何其他Python数组中一样,张量中的元素可以通过索引访问。
1、如用[-1]选择最后一个元素,用[1:3]选择第二个和第三个元素
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
print(X)
print(X[-1])
print(X[1:3])
结果展示:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
tensor([ 8., 9., 10., 11.])
tensor([[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
2、通过指定索引来将元素写入矩阵。
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
X[1, 2] = 9
print(X)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 9., 7.],
[ 8., 9., 10., 11.]])
3、如果我们想为多个元素赋值相同的值,我们只需要索引所有元素,然后为它们赋值。
例如,[0:2, :]访问第1行和第2行,其中“:”代表沿轴1(列)的所有元素。
虽然我们讨论的是矩阵的索引,但这也适用于向量和超过2个维度的张量。
(1) X[0:2, :]
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
X[0:2, :] = 12
print(X)
tensor([[12., 12., 12., 12.],
[12., 12., 12., 12.],
[ 8., 9., 10., 11.]])
(2) X[0:2, 2:4]
X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
X[0:2, 2:4] = 12
print(X)
tensor([[ 0., 1., 12., 12.],
[ 4., 5., 12., 12.],
[ 8., 9., 10., 11.]])
2.5、节省内存
运行一些操作可能会导致为新结果分配内存。
例如,如果我们用
Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
id() : 提供了内存中引用对象的确切地址
1、Y = Y + X
before = id(Y)
Y = Y + X
print(id(Y) == before) # False
这可能是不可取的,原因有两个:
- 首先,我们不想总是不必要地分配内存。 在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。 通常情况下,我们希望原地执行这些更新。
- 其次,如果我们不原地更新,其他引用仍然会指向旧的内存位置, 这样我们的某些代码可能会无意中引用旧的参数。
2、可以使用切片表示法将操作的结果分配给先前分配的数组
例如Y[:] = 。 为了说明这一点,我们首先创建一个新的矩阵Z,其形状与另一个Y相同, 使用zeros_like来分配一个全0的块。
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
结果展示:
id(Z): 140316199714544
id(Z): 140316199714544
3、如果在后续计算中没有重复使用X, 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
print(id(X) == before) # True
2.6、转换为其他Python对象
1、将深度学习框架定义的张量转换为NumPy张量(ndarray)很容易,反之也同样容易。
torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量。
A = X.numpy()
B = torch.tensor(A)
print(type(A), type(B))
(numpy.ndarray, torch.Tensor)
2、要将大小为1的张量转换为Python标量,我们可以调用item函数或Python的内置函数。
a = torch.tensor([3.5])
print(a, a.item(), float(a), int(a))
结果展示:
(tensor([3.5000]), 3.5, 3.5, 3)
3、数据预处理
3.1、读取数据
(1)创建数据
存储在csv文件
import os
# 1、创建数据集
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
(2)读取数据
要从创建的CSV文件中加载原始数据集,我们导入pandas包并调用read_csv函数。
data = pd.read_csv(data_file)
print(data)
结果展示:
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
进程已结束,退出代码为 0
3.2、除去缺失值
“NaN”项代表缺失值。
为了处理缺失的数据,典型的方法包括插值法和删除法
- 插值法用一个替代值弥补缺失值
- 删除法则直接忽略缺失值
在这里,我们将考虑插值法:
通过位置索引iloc,我们将data分成inputs和outputs, 其中前者为data的前两列,而后者为data的最后一列。 对于inputs中缺少的数值,我们用同一列的均值替换“NaN”项。
- 关键代码:
# 3、处理缺失值
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
# mean()函数功能:求取均值
# fillna() 使用指定的方法填充NA/NaN值。
- 运行结果:
NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
- 整体代码:
import os
import pandas as pd
# 1、创建数据集
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
# 2、读取数据
# 基于pandas
data = pd.read_csv(data_file)
print(data)
# 3、处理缺失值
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
# mean()函数功能:求取均值
# fillna() 使用指定的方法填充NA/NaN值。
print(inputs)
对于inputs中的类别值或离散值,我们将“NaN”视为一个类别。
由于“巷子类型”(“Alley”)列只接受两种类型的类别值“Pave”和“NaN”, pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。
巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。
缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
代码:
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
处理前:
NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
处理后:
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
3.3、转换为张量格式
现在inputs和outputs中的所有条目都是数值类型,它们可以转换为张量格式。
关键代码:
import torch
# 4、转换为张量格式
x, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(x)
print(y)
结果展示:
tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64)
tensor([127500, 106000, 178100, 140000])
PS:64位浮点数相对较占内存,我们平时使用中使用32位即可
完整代码:
import os
import pandas as pd
import torch
# 1、创建数据集
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
# 2、读取数据
# 基于pandas
data = pd.read_csv(data_file)
print(data)
# 3、处理缺失值
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
# mean()函数功能:求取均值
# fillna() 使用指定的方法填充NA/NaN值。
print(inputs)
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
# 4、转换为张量格式
x, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(x)
print(y)
02 线性代数
1、标量
我们称仅包含一个数值的叫标量(scalar)。
- 数学表示法中标量变量由普通小写字母表示(例如,x、y和z)
标量由只有一个元素的张量表示。 在下面的代码中,我们实例化两个标量:
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y
结果展示:
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))
2、向量
你可以将向量视为标量值组成的列表。 我们将这些标量值称为向量的元素(element)或分量(component)。
- 在数学表示法中,我们通常将向量记为粗体、小写的符号 (例如,x、y和z))
我们通过一维张量处理向量。一般来说,张量可以具有任意长度,取决于机器的内存限制。
x = torch.arange(4)
x
tensor([0, 1, 2, 3])
2.1、长度、维度和形状
- len(x)
- x.shape
示例程序:
import torch
x = torch.arange(4)
print(x)
print(x[3])
# 2.1、长度、维度和形状
print(len(x))
print(x.shape)
结果展示:
tensor([0, 1, 2, 3])
tensor(3)
4
torch.Size([4])
3、矩阵
- 创建矩阵
- 转置矩阵
- 对称矩阵
示例代码:
import torch
# 3、矩阵
A = torch.arange(20).reshape(5, 4)
print(A)
# 转置矩阵
print(A.T)
# 对称矩阵
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
print(B)
print(B == B.T)
运行结果:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
3.1、张量
就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构。 张量(本小节中的“张量”指代数对象)为我们提供了描述具有任意数量轴的n维数组的通用方法。 例如,向量是一阶张量,矩阵是二阶张量。 张量用特殊字体的大写字母表示(例如,X、Y和Z)
PS:
此时你可能会对“张量、标量、向量”的概念产生疑惑
当我们开始处理图像时,张量将变得更加重要,图像以n维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)
下面我们先学习一些张量的基础知识:
先创建一个张量:
X = torch.arange(24).reshape(2, 3, 4)
print(X)
结果展示:
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
3.2、张量算法的基本性质
1、同形状矩阵的二元计算
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
print(A)
print(A + B)
运行结果:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]])
2、Hadamard积
两个矩阵的按元素乘法称为Hadamard积
print(A * B)
运行结果:
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
3、张量*标量
将张量乘以或加上一个标量不会改变张量的形状
a = 2
A = torch.arange(24).reshape(2, 3, 4)
print(A + a)
print(a * A)
运行结果:
tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]])
tensor([[[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]],
[[24, 26, 28, 30],
[32, 34, 36, 38],
[40, 42, 44, 46]]])
4、降维
4.1、求和
import torch
import numpy as np
# x = np.arange(4)
# x,x.sum()
# 这里规避一个错误,我们调用的是 torch.arange() 而非 numpy ,否则后面代码花里胡哨的错误
x = torch.arange(4, dtype=torch.float32)
x, x.sum()x = np.arange(4)
x,x.sum()
运行结果:
(tensor([0., 1., 2., 3.]), tensor(6.))
我们可以表示任意形状张量的元素和
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A, A.shape, A.sum()
运行结果:
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
torch.Size([5, 4]),
tensor(190.))
4.2、降维
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。
我们还可以指定张量沿哪一个轴来通过求和降低维度。
(1)沿轴0
以矩阵为例,为了通过求和所有行的元素来降维(轴0),我们可以在调用函数时指定axis=0。
- 由于输入矩阵沿0轴降维以生成输出向量,因此输入轴0的维数在输出形状中消失。
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
运行结果:
(tensor([40., 45., 50., 55.]), torch.Size([4]))
(2)沿轴1
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
运行结果:
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))
(3)沿行和列
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。
A.sum(axis=[0, 1])
运行结果:
tensor(190.)
(4)求平均值
# 将总和除以元素总数来计算平均值
A.mean(), A.sum() / A.numel()
运行结果:
(tensor(9.5000), tensor(9.5000))
计算平均值的函数也可以沿指定轴降低张量的维度。
(tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))
4.3、非降维求和
有时在调用函数来计算总和或均值时保持轴数不变会很有用(或者说我们在运算时,不想把维度丢掉,想保持轴数不变)。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
"""
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
"""
sum_A = A.sum(axis=1, keepdims=True)
sum_A
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])
通过广播将A除以sum_A
A / sum_A
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
如果我们想沿某个轴计算A元素的累积总和, 比如axis=0(按行计算),我们可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。
A.cumsum(axis=0)
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
4.4 点积(Dot Product)
点积是相同位置的按元素乘积的和
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y) # 对 x, y两个张量,相同位置的按元素乘积,再求和
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积
x*y, torch.sum(x*y)
(tensor([0., 1., 2., 3.]), tensor(6.))tensor(6.)
4.5、矩阵-向量积
PS:
比如: α=(1,2,3), β=(4,5,6)
则 α, β的内积等于 1 * 4 +2 * 5 + 3 * 6 = 32
示例:
当我们为矩阵A和向量x调用torch.mv(A, x)时,会执行矩阵-向量积。 注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)
A, x ,A.shape, x.shape
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([0., 1., 2., 3.]),
torch.Size([5, 4]),
torch.Size([4]))
torch.mv(A, x)
tensor([ 14., 38., 62., 86., 110.])
4.6、矩阵-矩阵乘法
我们可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积,并将结果拼接在一起,形成一个n×m矩阵。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)
B, torch.mm(A, B)
(tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]),
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]]))
矩阵-矩阵乘法可以简单地称为矩阵乘法,不应与”Hadamard积”混淆。
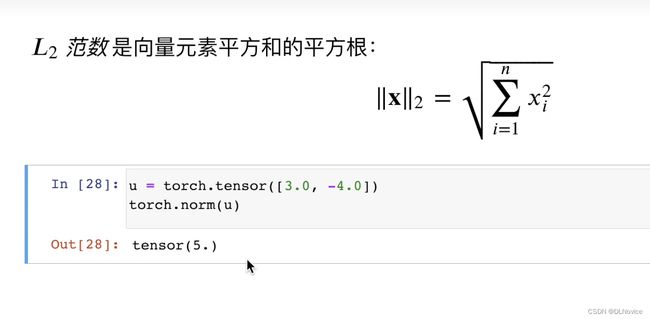
4.7、范数
- 向量的范数可以简单形象的理解为向量的长度,或者向量到零点的距离,或者相应的两个点之间的距离。
- 向量的范数定义:向量的范数是一个函数||x||,满足非负性||x||>=0,三角不等式||x+y||<=||x||+||y||。
范数在机器学习中的应用:
范数和L2范数,用于机器学习的L1正则化、L2正则化。对于线性回归模型,使用L1正则化的模型叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
参考博客:范数在深度学习中的应用 - 知乎 (zhihu.com)
4.7.1、范数和目标
在深度学习中,我们经常试图解决优化问题: 最大化分配给观测数据的概率; 最小化预测和真实观测之间的距离。 用向量表示物品(如单词、产品或新闻文章),以便最小化相似项目之间的距离,最大化不同项目之间的距离。 目标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数。
补充:按特定轴求和
视频链接:按特定轴求和_哔哩哔哩_bilibili
4、线性代数QA
视频链接:线性代数 QA_哔哩哔哩_bilibili
选择框架,学pytorch or tensorflow or …?
==》 学开车,选什么车都行,每隔一个时段都有新的流行的工具产生,会用工具,而不限制于工具
5、小结
- 标量、向量、矩阵和张量是线性代数中的基本数学对象。
- 向量泛化自标量,矩阵泛化自向量。
- 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
- 一个张量可以通过
sum和mean沿指定的轴降低维度。 - 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。
- 在深度学习中,我们经常使用范数,如L1范数、L2范数和Frobenius范数。
- 我们可以对标量、向量、矩阵和张量执行各种操作。
03 微积分
- 1. 导数和微分
- 2. 偏导数
- 3. 梯度
- 4. 链式法则
- 5. 小结
- 6. 练习
04 自动微分
- 1. 一个简单的例子
- 2. 非标量变量的反向传播
- 3. 分离计算
- 4. Python控制流的梯度计算
- 5. 小结
- 6. 练习
05 概率
-
- 基本概率论
- 1.1. 概率论公理
- 1.2. 随机变量
-
- 处理多个随机变量
- 2.1. 联合概率
- 2.2. 条件概率
- 2.3. 贝叶斯定理
- 2.4. 边际化
- 2.5. 独立性
- 2.6. 应用
-
3. 期望和方差
-
4. 小结
-
5. 练习
06 查阅文档
- 1. 查找模块中的所有函数和类
- 2. 查找特定函数和类的用法
- 3. 小结
- 4. 练习