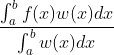数学分析-一元微积分
1. 点集拓扑预备知识
(1)集合基础:包含关系、交并补、笛卡尔积运算、交换律/结合律/分配律/De-Morgan定律、集合的势cardX(两集合等势表示集合之间存在双射)、元素可数(表示与自然数集等势)、幂集![]() (由X的一切子集构成的集)
(由X的一切子集构成的集)
(2)Cantor定理:![]() 。证明思路用反证法,假设
。证明思路用反证法,假设![]() 是双射,构造并分析集合
是双射,构造并分析集合![]() 中的元素,引发与双射的矛盾。
中的元素,引发与双射的矛盾。
(3)度量空间(X, d):度量(也叫距离)d: ![]() 的定义,需要满足正则性、对称性、三角不等式d(x, z)<=d(x, y) + d(y, z)。例如对Euclidean空间
的定义,需要满足正则性、对称性、三角不等式d(x, z)<=d(x, y) + d(y, z)。例如对Euclidean空间![]() ,可用向量距离d(x, y)=|x-y|作为一个度量。
,可用向量距离d(x, y)=|x-y|作为一个度量。
(4)内点/边界点/聚点/孤立点/导集/闭包:
内点:表示存在p的邻域![]() 全部包含在集合E中。直观上表示该点周围都围满了其他在该集合中的点。
全部包含在集合E中。直观上表示该点周围都围满了其他在该集合中的点。
边界点:表示任一邻域中至少有一个点在E中,且至少有一个点不在E中。注意边界点不一点属于E。E的边界点组成的集合叫作边界,记作![]() 。
。
聚点(极限点):p为集E的聚点,表示p的任一邻域内至少有异于p的一点在E中。这说明E中至少有一个无穷点列趋近于p。注意聚点并一定属于E,E的所有聚点构成E的导集![]() ,E并上E的聚点构成E的闭包
,E并上E的聚点构成E的闭包![]() 。注意欧氏空间中的内点一定是聚点,但一般拓扑空间中的内点就不一定是聚点(因为它有可能是孤立点)。反过来,聚点也不一定是内点。
。注意欧氏空间中的内点一定是聚点,但一般拓扑空间中的内点就不一定是聚点(因为它有可能是孤立点)。反过来,聚点也不一定是内点。
孤立点:E中的非聚点称为E的一个孤立点。即存在一个邻域,其中不含E中除x的其他点。直观上表示该点在集合中被孤立,但是还没离队。欧氏空间中的孤立点一定是边界点,但一般拓扑空间中的孤立点就不一定是边界点。反过来,集合的边界点也不一定是孤立点。
(5)开集:集合中的点全部为内点。
(6)闭集/完全集:即聚点都在集合E内。另外若聚点都在集合内,且集合内的所有点都是聚点,则称为完全集。
(7)有界/稠密:有界表示存在一个圈,使得E中所有点都在这个圈内。即![]() ,则称E有界。注意x和r是事先固定。
,则称E有界。注意x和r是事先固定。
稠密表示X的所有点都是E的聚点或E的点,即![]() ,则称E在X中稠密。直观上稠密表示X的任何局部(即开子集)都有E中的点,E充满了X的各个地方,但E在X中可能还有"缝隙"。
,则称E在X中稠密。直观上稠密表示X的任何局部(即开子集)都有E中的点,E充满了X的各个地方,但E在X中可能还有"缝隙"。
(8)开覆盖:是一个开集序列![]() ,它的并集能覆盖E。任一集合的开覆盖总是存在的。
,它的并集能覆盖E。任一集合的开覆盖总是存在的。
(9)紧集:集合的任意开覆盖都含有至少一个有限子覆盖(覆盖中只含有有限个集合)。注意紧集是用集合的有限开覆盖来定义的,一般拓扑中没有度量结构,怎么定义紧呢?拿开集去覆盖,就只需要有限多个。换言之,每一点都找一个开领域,那么只需要有限多个即可,其它的紧紧地围绕在他们身边。与极限类似,集合覆盖这种概念的引入体现的也是外部变化过程+无限逼近的思想。只不过极限是用一个点列去逼近某个数学对象,覆盖则是用一个集合序列通过不断相套夹逼这种“外部挤压”的方式去逼近某个数学对象。一个对象不好做数学定义和研究时(比如对它有什么好的性质一无所知),可以外部化,附加上某些已知的结构,或者“外部挤压”的方式去定义和研究它。
(10)格(矩形):取![]() ,
,![]() 中的集合
中的集合![]() 称为一个k-格。格可以理解为高维的矩形,一维k-格是闭区间,2维则是矩形,3维立方体,以此类推。实际上它是这k个闭区间集合的笛卡尔积
称为一个k-格。格可以理解为高维的矩形,一维k-格是闭区间,2维则是矩形,3维立方体,以此类推。实际上它是这k个闭区间集合的笛卡尔积 ![]() 。定义它的体积
。定义它的体积 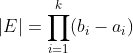 ,定义正方体为满足
,定义正方体为满足![]() 的矩形。
的矩形。
(11)分离/连通:集合A和B是分离的,表示![]() (这里
(这里![]() 是A的闭包)。反之,若
是A的闭包)。反之,若![]() 或者
或者![]() ,则称集合A与B连通。集合"相离”这个条件要比“不交”强一点,它相当于两集合不交中“相贴”的情况也去掉了。例如[0, 1]和(1, 2)不交,但却是连通的,而(0, 1)与(1, 2)则是分离的。
,则称集合A与B连通。集合"相离”这个条件要比“不交”强一点,它相当于两集合不交中“相贴”的情况也去掉了。例如[0, 1]和(1, 2)不交,但却是连通的,而(0, 1)与(1, 2)则是分离的。
(12)连通集:实数域R上的E为连通集 ![]()
![]() 。
。
(13)主要定理:
(13.1)开集闭集的性质:任意邻域都是开集。聚点的任一邻域都有无穷多个点在E里,即![]() ,有
,有![]() 为无限集。任一有限集都不含有聚点。E为开集
为无限集。任一有限集都不含有聚点。E为开集![]()
![]() 为闭集。
为闭集。
(13.2)开集闭集的运算:对开集序列有限交运算封闭(仍为开集),任意并运算(有限或无限)也封闭。对闭集序列有限并运算封闭(仍为闭集),任意交运算封闭。
(13.3)闭包性质:闭包![]() 为闭集,且是包含E的"最小"闭集。
为闭集,且是包含E的"最小"闭集。![]() 为闭集。
为闭集。
(13.4)紧集性质:度量空间内所有的紧集都是闭集。紧集的闭子集仍然是紧集。闭集与紧集的交是紧集。任一k-格都是紧集。
(13.5)Cantor区间套定理:无限的非空紧集序列若构成一个区间套(即前一个紧集覆盖后一个紧集),则这个紧集序列的交是非空的;另外若这个区间套中的紧集越来越小(度量直径趋于0),则交集中只含一个点。(推论)特别地,实数系R上的任一无限闭区间套的交是非空的,并且含有唯一的一个实数。任一无限k-格区间套的交集是非空的。
(f)Heine-Borel有限覆盖定理:![]() 上的子集E为紧集等价于E为有界闭集。特别地,R上的任一个闭区间都是紧集。
上的子集E为紧集等价于E为有界闭集。特别地,R上的任一个闭区间都是紧集。
(g)Bolzano-Weierstrass聚点定理:紧集中的任一无限子集至少存在一个聚点。特别地,![]() 的任一有界无限子集都有聚点。注意聚点定理可用区间套定理来证明。
的任一有界无限子集都有聚点。注意聚点定理可用区间套定理来证明。
(h) (14)拓扑空间:对集合X上的一个子集族 (15)拓扑的基:是一个子集族B(其中每个子集称为基元素),它遍历X中的每个元素(即X的每个元素 (16)滤子/滤子基:X的滤子是一个非空子集族E,其中单一交封闭,单一覆盖也封闭( (17)集合直径(长度): 集合的距离: 点到集合的距离: 2. 极限ε-δ语言 变化过程+无限逼近的思想。用一个变化过程(离散或连续的点列)无限接近一个数学对象。 (1)数列极限/数列收敛: (2)数列上下极限:上极限为广义子列极限的最大者(即极限可能是 (3)函数极限:f是度量空间X的子集E到度量空间Y的一个映射,函数极限 x->∞的函数极限:则是 含义:无论事先给定多么小的正数ε,总可以找到一个正数δ,当x在a的去心邻域U(a, δ)内变化,f(x)与a的距离都小于ε。关键是根据确定的ε去找到这个δ,通常δ是ε和a的函数。这里0<|x-a|<δ表示x的变化过程(去心邻域),|f(x)-a|<ε表示函数与点a无限接近。这些定义说明极限存在的必要条件是“对于任意小的误差范围总可以找到相应的缩放级别”,这个条件保证了不会漏掉“中途被外星人吸走又放回去”的情况。 几何意义:当点x一旦进入到a的充分小的去心邻域时,它的像点f(x)就落入到b的一个预先给定的ε邻域中。 极限这个概念的严格化是分析的基础。导数、微分、连续、积分、级数收敛等等概念,都是用极限来定义的。函数极限的ε-δ定义第一次使极限和连续性摆脱了与几何和运动的任何牵连,给出了只建立在数与函数概念上的清晰的定义,从而使一个模糊不清的动态描述,变成为一个严密叙述的静态观念,这不能不认为是变量数学史上的一次重大创新。今天ε-δ语言的精髓已经深入到现代数学的每一根血管,牵动着每一根神经。注意ε-δ定义的极限离不开度量概念,所以只适用于度量空间。对于非度量空间,在拓扑学发展的基础上,发展出了用开集、滤子等去定义极限。 (4)Cauchy列(基本列): 完备空间/Cauchy空间:任一Cauchy列都收敛的度量空间。 致密集(列紧集):E是致密集,表示E中任何点列都有子列收敛于度量空间X中的某点。注意该点不一定在该致密集中。 (5)极限的性质:唯一性、有界性、局部保号性、保不等式性 (6)极限存在性的判定: (6.1)夹逼定理(挤压定理):对数列,从某项开始, (6.2)度量空间中任一数列子列极限组成的集合都是闭集。致密的闭集是紧集。度量空间中的任意收敛数列都是Cauchy列。 (6.3)Bolzano-Weierstrass致密性定理:紧度量空间中的数列必有收敛子列。特别地, (6.4)Cauchy收敛原理:紧度量空间中的数列收敛等价于该数列是Cauchy列。特别地, (6.5)单调有界定理:实数域的单调数列收敛等价于有界。作为一个应用,可用于证明 (6.6)Heine定理: (8)实数的完备性(连续性):完备性公理是戴德金原理,另外7个连续性基本定理是确界原理、单调有界定理、闭区间套定理、有限覆盖定理、聚点定理、致密性定理、Cauchy收敛原理。这8个定理是等价的。可以互相推出,它们通过不同的数学处理方法,揭示了实数系R具有完备性(连续性)。 戴德金原理:对R中的任何两个非空子集划分A和B(即A中的实数a小于B中的实数),存在实数c,对任意的 确界原理:R中有上界(下界)的子集必有上确界(下确界),记作sup S(inf S)。它与戴德金原理是等价的。 3. 级数 (1)级数收敛的必要条件:级数的项趋于0。即级数 (2)Cauchy准则判别法:级数收敛的充要条件是对任意的 (3)Weierstrass比较判别法:若从某项开始恒有 (4)Cauchy根值判别法:对项根值的上极限 (5)D'Alembert比值判别法:对相邻项比值的上极限 (6)正项级数:收敛的充要条件是部分和数列有界。特别地,对单调递减的正项级数 (7)乘项级数 (8)Leibnitz定理:应用于交错级数(正项和负项交替出现的级数)。若数列 (10)调和级数 (11)黎曼zeta函数: (12)Mertens定理:应用于级数的乘积,两个级数的Cauchy乘积 (13)Abel定理:若级数 (14)级数重排:若级数 (15)Riemann定理:若 下面讨论复数项级数: (1)棣莫弗公式:对复数的三角表示 (2)复数列收敛到 (3)复数列收敛的柯西准则:复数列收敛当且仅当它是基本列。也就是对于任意的 (3)Cauchy–Hadamard定理(幂级数收敛定理):幂级数 (4)阿贝尔第一定理:若幂级数 (5)若幂级数 (6)若复数级数绝对收敛,则它的任意重排都收敛到同一个和。绝对收敛级数的乘积是绝对收敛级数,它的和等于二者和的积。 (7)欧拉公式: 4. 函数连续性 (1)函数连续的定义:y=f(x)是度量空间X到Y的一个映射,连续定义为 (2)函数连续的充要条件:Y=f(X)连续,等价于对Y中的任意开集V,其逆像 (3)连续函数的性质:局部有界性、局部保号性、局部保不等式性 (4)闭区间上连续函数的性质:有界定理(有最大值最小值)、介值定理(函数可以取两端点内的一切值)、零点定理(两端点异号则必存在零点)、一致连续定理(闭区间上连续等价于一致连续)。这些定理可以使用确界原理、区间套定理、有限覆盖定理、聚点定理等加以证明。 (5)初等函数连续性:常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数,以及经过有限次四则运算与复合运算得到函数。一切初等函数在其定义域上都是连续函数。 (6)Dirichlet函数: (7)Riemann函数: (8)间断点:单调函数的间断点个数至多可数。 5. 微分学 (1)导数/微分:像点对原像点的变化率。可导定义为 几何意义:导数为函数图像上该点处切线的斜率。切线方程 物理意义:例如位移对时间的变化率,表示速度。 复变函数的连续、导数、微分也是类似地定义。 (2)微分学基本定理(MVT定理): 微分中值定理反映函数与和导数/微分之间的联系,是沟通两者的桥梁。 (2.1)Rolle中值定理:闭区间[a, b]上连续,开区间(a, b)上可微,两端点处函数值相等f(a)=f(b),则在开区间(a, b)上存在一点c的导数为0, (2.2)Lagrange中值定理:闭区间[a, b]上连续,开区间(a, b)上可微,则在开区间(a, b)上存在一点c,有 (2.3)Cauchy中值定理:f(x), g(x)在[a, b]上连续,在(a, b)上可微,则在(a, b)上至少存在一点c,有 (2.4)Taylor定理:函数f(x)在 根据泰勒定理,如果函数无穷可微,可以将某定义域内的一般函数f(x)展开成多项式表示的泰勒级数,但是该级数不一定收敛,即使收敛也不一定收敛到f(x)的值。一些函数无法被展开为泰勒级数,因为那里存在一些奇点。但是如果变量x是负指数幂的话,仍然可以将其展开为一个级数。例如 例子:由 (2.5)Darboux定理:f(x)在闭区间[a, b]上可微,则其导函数 (3)洛必达法则:0/0型不定式求极限,在(a, b)上,f(x)和g(x)都可微、g′(x) ≠ 0, (4)用微分学方法研究函数: (4.1)函数单调性:一阶导为正,函数递增;一阶导为负,函数递减。 (4.2)函数极值:极值点必要条件是不可导或一阶导为0(称为稳定点)。若左侧邻域导数为负右侧邻域导数为正则是极小值;若左侧邻域导数为正右侧邻域导数为负则是极大值。若n-1阶导为0,n阶导不为0,则n为奇数时无极值,n为偶数时有极值,且n阶导为负时是极大值,n阶导为正时是极小值。 (4.3)函数凹凸性:二阶导恒>=0,则下凸;二阶导恒<=0,则下凹。 (5)用微分学方法研究不等式: 不等式是做放缩、挤压处理的基本技巧,分析中的大量命题都是通过放缩、挤压来进行证明的。 (5.1)Bernoulli不等式:对实数 等号成立当且仅当a=0,1,或x=-1时。伯努利不等式是从幂函数到一次函数的放缩,经常用作证明其他不等式的关键步骤。y=1+ax可视为 (5.2)Young不等式:若 (5.3)Holder不等式:若 当且仅当向量 (5.4)Minkowski不等式:若 当且仅当向量 (5.6)均值不等式:调和平均 (6)复数项幂级数的可微性:幂级数 (7)代数基本定理:每个次数大于等于1的复系数多项式 下面讨论不定积分(导数的逆运算): (1)线性性质: (2)分部积分: (3)换元积分: (3.1)凑微分法:若f(u)具有原函数,u又是另一变量的函数 它表明若f(x)能凑成 (3.2)变量替换法:若f(x)有原函数,对积分变量x作代换 它表明通过变量代换把求f(x)的积分转化成求 (4)三角代换:对有二次根式的积分,常常作三角代换 (5)正弦积分/余弦积分/对数积分: (6)有理函数积分: (7) (8) (9)椭圆积分:形如 6. 积分学 (1)Lebesgue外测度:所有矩形覆盖(每个覆盖有至多可数的集合)的体积值的下确界,记作 外测度的性质:非负性、单调性、次可加性 体积值|A|:对点集A指定的一个非负实数,其定义不受限制。通常一维闭区间[a, b]的体积值 (2)Lebesgue测度:对任意 勒贝格可测集的基本性质:可测集的可列交、并、补都封闭。可列可加性。任意 (3)勒贝格零测集的等价定义:对任意 零测集的性质:有限或可数个点构成的集合是零测集。零测集的可列并、可列交都封闭。零测集的子集是零测集。 (4)函数振幅:函数在集合上的振幅为E的所有像点距离的最大值,即 (5)区间的划分(分割):在闭区间[a, b]上,一个有限点列表示一个划分P,其中 (6)划分的延拓:对取样划分 (7)黎曼和(积分和):在[a, b]上,函数f一个取样划分(P,t),黎曼和为 (8)黎曼积分:所有取样划分长度趋于0时的黎曼和极限。对函数f在闭区间[a, b]上的任意一个取样划分(P, t),当长度 更具可操作性的等价定义:对任意的 (9)可积的必要条件:函数f在[a, b]上有界。 (10)可积的充分条件:对任意的 可见,当函数值急剧变化,使函数振幅不变小的区间很多时,就会有Riemann不可积的情况发生。由此可证Dirichlet函数不可积。因为它在每个小区间上的振幅都是1。 (11)函数可积的充要条件:当且仅当f(x)有界,且对任意的划分P,都有 (12)Riemann–Lebesgue定理:函数f在闭区间[a, b]上可积,当且仅当它在[a, b]上有界,且间断点集是勒贝格零测集。 推论:闭区间上连续函数可积。闭区间上的有界函数若只有可数个间断点则可积。闭区间上的单调函数可积。 由此可见,Riemann函数是可积的,因为它有界,间断点集可数,是零测集。 (13)积分第一中值定理:若函数f在[a, b]上连续,则存在点 积分中值定理反映函数与函数积分之间的联系,是沟通两者的桥梁。 (14)积分第二中值定理:在[a, b]上,若f, g可积,且g单调,则存在点 (15)原函数存在定理:闭区间上的连续函数f(x)一定有原函数,且都是 (16)在闭区间上,若函数f(x)有界,且只有有限个间断点,则它有广义的原函数F(x)(即只在有限个点处 (17)牛顿-莱布尼茨公式:如果函数f(x)在闭区间[a, b]上有界,并且只有有限个间断点,则f(x)在[a, b]上可积,且 证明思路定义变上限积分函数,利用函数导数定义和积分中值定理将积分的计算与原函数联系起来。 (17)分部积分公式: (18)定积分的应用: (18.1)空间曲线(道路):空间 (18.2)两条曲线围成的面积:微分 (18.3)旋转体体积:曲线f(x)绕x轴旋转一周形成的旋转体,用圆盘法, 绕y轴旋转一周的旋转体,用柱壳法, (18.4)曲线长度: (18.5)旋转体表面积: (18.6)曲线平均值: 下面讨论反常积分(变上限积分): (1)反常积分:对有限或无限区间[a, t),函数f(x)在每个子区间 (2)反常积分柯西判别法:反常积分 由柯西判别法知,绝对收敛的反常积分必收敛,那么对绝对收敛性的研究就化为对非负函数的积分收敛性研究。 (3)级数收敛积分准则:若f(x)定义在 (4)阿贝尔-狄利克雷准则:f(x), g(x)在[a, t)的每个子区间上可积,g(x)是单调函数,则 ![]() 中的任一非空完全集不可数。推论R上任一区间 [a, b] 不可数。card N
中的任一非空完全集不可数。推论R上任一区间 [a, b] 不可数。card N![]() ,它包含空集和X,其中的有限交封闭(有限个集合的交仍在
,它包含空集和X,其中的有限交封闭(有限个集合的交仍在![]() 中),任意并也封闭,则
中),任意并也封闭,则![]() 称为X上的一个拓扑,(X,
称为X上的一个拓扑,(X, ![]() )为拓扑空间。若
)为拓扑空间。若![]() ,则称A是该拓扑空间中的一个开集。若
,则称A是该拓扑空间中的一个开集。若![]() ,则称A是该拓扑空间中的一个闭集。开(闭)集是相对拓扑空间而言的,在这个拓扑空间里它是开(闭)集,可能它在另一个拓扑空间中就不是开(闭)集了。另外从闭集的定义可以看出所谓开集和闭集只是对同一拓扑空间的不同描述,因为一个空间,你只要定义了什么是闭集(就是全部闭集组成的集族是啥),自然也就定义了什么叫开集。
,则称A是该拓扑空间中的一个闭集。开(闭)集是相对拓扑空间而言的,在这个拓扑空间里它是开(闭)集,可能它在另一个拓扑空间中就不是开(闭)集了。另外从闭集的定义可以看出所谓开集和闭集只是对同一拓扑空间的不同描述,因为一个空间,你只要定义了什么是闭集(就是全部闭集组成的集族是啥),自然也就定义了什么叫开集。![]() 都属于某个基元素),并且若有两个基元素
都属于某个基元素),并且若有两个基元素![]() 都包含
都包含![]() 时,存在一个包含元素
时,存在一个包含元素![]() 的嵌套基元素
的嵌套基元素![]() 。
。![]() 时有
时有![]() )。仅有单一交封闭时称为滤子基(简称为基)。
)。仅有单一交封闭时称为滤子基(简称为基)。![]() ,即E中“最大”的距离。
,即E中“最大”的距离。![]() ,即两个集合间“最小”的距离。
,即两个集合间“最小”的距离。![]()
![]() ,称数列
,称数列![]() 收敛于a。数列收敛于a等价于每个子列都收敛于a。
收敛于a。数列收敛于a等价于每个子列都收敛于a。![]() ),即全部广义子列极限组成的集合的上确界,即
),即全部广义子列极限组成的集合的上确界,即![]() 。下极限为广义子列极限的最小者,即全部广义子列极限组成的集合的下确界,即
。下极限为广义子列极限的最小者,即全部广义子列极限组成的集合的下确界,即![]() 。
。![]() 定义为,对于
定义为,对于![]() ,使得
,使得![]() 。注意a是聚点是相当重要的一个条件,如果不是聚点,就不能谈极限了,因为我们甚至有可能到找不到满足
。注意a是聚点是相当重要的一个条件,如果不是聚点,就不能谈极限了,因为我们甚至有可能到找不到满足![]() 的点x了。特别地,对实数系内的函数有
的点x了。特别地,对实数系内的函数有![]()
![]() ,这时去心邻域是|x|>δ。例如x->∞时,有sinx/x->0。
,这时去心邻域是|x|>δ。例如x->∞时,有sinx/x->0。![]() 。注意在一般度量空间中,基本列不一定收敛,基本列是收敛数列的弱化版。
。注意在一般度量空间中,基本列不一定收敛,基本列是收敛数列的弱化版。![]() ,并且
,并且![]() ,则
,则![]() 极限存在,且
极限存在,且![]() 。求数列或函数极限的基本方法,通过不等式放缩构造,再运用夹逼定理。
。求数列或函数极限的基本方法,通过不等式放缩构造,再运用夹逼定理。![]() 中的任意有界数列必存在收敛子列。注意致密性定理可由聚点定理直接推出,并且可知数列的任一聚点对应一个子列的极限,因此聚点也叫极限点。
中的任意有界数列必存在收敛子列。注意致密性定理可由聚点定理直接推出,并且可知数列的任一聚点对应一个子列的极限,因此聚点也叫极限点。 ![]() 中的数列收敛等价于它是Cauchy列。由此可知,紧度量空间与Euclidean空间都是完备的。
中的数列收敛等价于它是Cauchy列。由此可知,紧度量空间与Euclidean空间都是完备的。![]() 。
。![]() 存在,等价于对任何定义域内收敛于
存在,等价于对任何定义域内收敛于![]() ,且每项恒不为
,且每项恒不为![]() 的数列
的数列![]() ,都有
,都有![]() 。海涅定理也叫归结原理,是沟通函数极限和数列极限之间的桥梁。求函数极限则可化为求数列极限,同样求数列极限也可转化为求函数极限。因此,函数极限的所有性质都可用数列极限的有关性质来加以证明。
。海涅定理也叫归结原理,是沟通函数极限和数列极限之间的桥梁。求函数极限则可化为求数列极限,同样求数列极限也可转化为求函数极限。因此,函数极限的所有性质都可用数列极限的有关性质来加以证明。![]() 和
和![]() 都有
都有![]() 。
。
![]() 收敛,则
收敛,则![]() 。
。![]() ,存在N,对任意的
,存在N,对任意的![]() ,都有
,都有 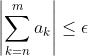 。
。![]() ,且级数
,且级数 ![]() 收敛,则级数
收敛,则级数 ![]() 绝对收敛。若从某项开始恒有
绝对收敛。若从某项开始恒有![]() ,且
,且 ![]() 发散,则
发散,则 ![]() 发散。
发散。![]() ,q<1时级数绝对收敛,q>1时级数发散,q=1时无结果。
,q<1时级数绝对收敛,q>1时级数发散,q=1时无结果。![]() ,q<1时级数绝对收敛,q>1时级数发散,q=1时无结果。
,q<1时级数绝对收敛,q>1时级数发散,q=1时无结果。![]() ,其收敛的充要条件是级数
,其收敛的充要条件是级数 ![]() 收敛。本定理可以将一些级数转化成几何级数来判别。
收敛。本定理可以将一些级数转化成几何级数来判别。![]() :若
:若![]() 的部分和数列有界,
的部分和数列有界,![]() 单调递减,且
单调递减,且![]() ,则乘项级数收敛。注意这只是一个充分条件。
,则乘项级数收敛。注意这只是一个充分条件。![]() 单调递减,且
单调递减,且![]() ,则交错级数收敛。
,则交错级数收敛。![]() :调和级数发散。对一般级数
:调和级数发散。对一般级数 ![]() ,
,![]() 时收敛,
时收敛,![]() 时发散。证明思路通过放缩转化成几何级数。
时发散。证明思路通过放缩转化成几何级数。![]() ,这里s为复数,与黎曼猜想有关系。
,这里s为复数,与黎曼猜想有关系。![]() 就是调和级数,
就是调和级数,![]() ,求解
,求解![]() 这个问题被称为巴塞尔问题,目前已经有很多种不同的证明。
这个问题被称为巴塞尔问题,目前已经有很多种不同的证明。![]() 定义为
定义为 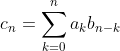 。对任意两个收敛的级数,如果它们中有一个级数绝对收敛,它们Cauchy乘积的和就是它们和的乘积。
。对任意两个收敛的级数,如果它们中有一个级数绝对收敛,它们Cauchy乘积的和就是它们和的乘积。![]() ,
,![]() ,以及Cauchy乘积
,以及Cauchy乘积![]() 分别收敛于A,B,C,则C=AB。
分别收敛于A,B,C,则C=AB。![]() 绝对收敛,则它的任意重排都收敛于同一值。特别地,正项级数收敛等价于它的所有重排都收敛于同一个值。
绝对收敛,则它的任意重排都收敛于同一值。特别地,正项级数收敛等价于它的所有重排都收敛于同一个值。![]() 条件收敛,则{
条件收敛,则{ ![]() 全部重排的和 }=
全部重排的和 }=![]() 。
。![]() ,有
,有![]() ,r为复数模长
,r为复数模长![]() ,θ为复数幅角
,θ为复数幅角 ![]() 。利用它可以得到一些三角函数高次幂与倍角公式。
。利用它可以得到一些三角函数高次幂与倍角公式。![]() ,是指
,是指 ![]() 。复数是复平面上的点,因此度量空间的收敛定理也都适用于复数列。一般地有,复数列收敛当且仅当它的项的实部和虚部的序列都收敛。
。复数是复平面上的点,因此度量空间的收敛定理也都适用于复数列。一般地有,复数列收敛当且仅当它的项的实部和虚部的序列都收敛。![]() ,存在正整数N,使得对于任意 m>n>N,都有
,存在正整数N,使得对于任意 m>n>N,都有![]() 。
。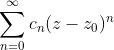 在以点
在以点![]() 为中心,以R为半径的圆
为中心,以R为半径的圆 ![]() 内收敛,其中R按阿达马公式确定
内收敛,其中R按阿达马公式确定 ![]() 。在这个圆的外部任何点处幂级数都发散;在这个圆的任何内点处幂级数绝对收敛。在
。在这个圆的外部任何点处幂级数都发散;在这个圆的任何内点处幂级数绝对收敛。在 ![]() 时无法判定级数收敛或发散。可用柯西根值判别法来证明。
时无法判定级数收敛或发散。可用柯西根值判别法来证明。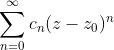 在某个点
在某个点![]() 处收敛,则它对任意满足
处收敛,则它对任意满足 ![]() 的点都绝对收敛。
的点都绝对收敛。![]() 的收敛半径为1,且
的收敛半径为1,且![]() 单调递减,
单调递减,![]() ,则幂级数在单位圆
,则幂级数在单位圆 ![]() 上除却z=1两点外的每一点都收敛。
上除却z=1两点外的每一点都收敛。![]() 。可以得到关系
。可以得到关系 ![]() ,复数的指数表示
,复数的指数表示 ![]() 。可以用exp z,cos z,sin z的泰勒级数展开来推导出欧拉公式。
。可以用exp z,cos z,sin z的泰勒级数展开来推导出欧拉公式。
![]() ,等价的定义
,等价的定义![]() 。另外也可以写成对点
。另外也可以写成对点![]() 处的任意邻域
处的任意邻域![]() ,都存在点
,都存在点![]() 处的邻域
处的邻域![]() ,满足
,满足![]() 。注意
。注意![]() 必须为X的聚点,f必须在
必须为X的聚点,f必须在![]() 处有定义。而收敛则不需要。
处有定义。而收敛则不需要。![]() 在X中也是开集。类似地,也等价于对Y中的任意闭集V,其逆像
在X中也是开集。类似地,也等价于对Y中的任意闭集V,其逆像![]() 在X中也是闭集。
在X中也是闭集。![]() ,它在所有点都间断,且都是第二类间断点(左右极限至少有一个不存在)。
,它在所有点都间断,且都是第二类间断点(左右极限至少有一个不存在)。![]() ,它在任意无理点处连续,在有理点处是第一类间断点(左右极限都存在但至少有一个与函数值不相等)。
,它在任意无理点处连续,在有理点处是第一类间断点(左右极限都存在但至少有一个与函数值不相等)。
![]() ,可导表示左导数和右导数都存在并且相等。对自变量的微小扰动如果有
,可导表示左导数和右导数都存在并且相等。对自变量的微小扰动如果有 ![]() ,其中A(x)h是h的线性函数,g(h)=A(x)h称为f在点x处的微分,记作
,其中A(x)h是h的线性函数,g(h)=A(x)h称为f在点x处的微分,记作![]() 。可微与可导是等价的。记作
。可微与可导是等价的。记作![]() ,微分的本质是一个函数在局部可以用简单的线性函数去逼近它。
,微分的本质是一个函数在局部可以用简单的线性函数去逼近它。![]()
![]() 。直观理解存在一点处的切线平行于两端点的水平直线。
。直观理解存在一点处的切线平行于两端点的水平直线。![]() 。直观理解存在一点处的切线平等两端点的连线。证明思路根据曲线上的点与连线的y轴距离构造辅助函数,运用罗尔定理。
。直观理解存在一点处的切线平等两端点的连线。证明思路根据曲线上的点与连线的y轴距离构造辅助函数,运用罗尔定理。![]() 。证明思路构造辅助函数用拉格朗日中值定理。
。证明思路构造辅助函数用拉格朗日中值定理。![]() 处的泰勒多项式为
处的泰勒多项式为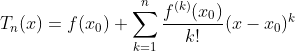 。若f(x)在[a, b]上有n阶连续的导函数,在(a, b)上有n+1阶导函数,则对任意的
。若f(x)在[a, b]上有n阶连续的导函数,在(a, b)上有n+1阶导函数,则对任意的 ![]() ,在x和
,在x和![]() 之间至少存在一点,使得
之间至少存在一点,使得 ![]() 。泰勒定理是拉格朗日中值定理的推广,它表明可以用多项式函数逼近一般的函数。
。泰勒定理是拉格朗日中值定理的推广,它表明可以用多项式函数逼近一般的函数。![]() 可以展开为一个洛朗级数。
可以展开为一个洛朗级数。![]() 的泰勒级数展开可推出
的泰勒级数展开可推出![]() ,因为
,因为![]() 的泰勒级数收敛到
的泰勒级数收敛到![]() 。
。![]() 在[a, b]上具有介值性,可以取到
在[a, b]上具有介值性,可以取到![]() 与
与![]() 之间的一切值。达布定理比连续函数的介值定理更强,因为
之间的一切值。达布定理比连续函数的介值定理更强,因为![]() 不一定是连续的。有原函数的函数(不一定要连续)就满足介值性。达布定理是原函数存在的一个必要条件。(推论)有介值性的函数没有第一类间断点。
不一定是连续的。有原函数的函数(不一定要连续)就满足介值性。达布定理是原函数存在的一个必要条件。(推论)有介值性的函数没有第一类间断点。![]() ,如果
,如果 ![]() ,则有
,则有![]() 。对
。对![]() 型不定式的极限也有类似的法则。
型不定式的极限也有类似的法则。![]() ,有
,有![]()
![]() 的切线。证明思路构造函数求极值,以确定不等号的方向。
的切线。证明思路构造函数求极值,以确定不等号的方向。![]() ,则
,则 ![]() ,当且仅当
,当且仅当![]() 时等号成立。当p<1且不为0时,不等式
时等号成立。当p<1且不为0时,不等式![]() 变为
变为![]() 。杨氏不等式是加权算术-几何平均值不等式的特例。证明思路根据函数lnx的凹凸性及凹凸性的定义来证明。
。杨氏不等式是加权算术-几何平均值不等式的特例。证明思路根据函数lnx的凹凸性及凹凸性的定义来证明。![]() ,则有
,则有![]() 与
与![]() 共线时等号成立。当p<1且不为0时,不等式
共线时等号成立。当p<1且不为0时,不等式![]() 变为
变为![]() 。可用杨氏不等式通过累加的方式来证明。有离散形式和积分形式赫尔德不等式。这是一条揭示Lp空间相互关系的基本不等式。
。可用杨氏不等式通过累加的方式来证明。有离散形式和积分形式赫尔德不等式。这是一条揭示Lp空间相互关系的基本不等式。![]() ,则有
,则有![]()
![]() 与
与![]() 共线时等号成立。当p<1且不为0时,不等式
共线时等号成立。当p<1且不为0时,不等式![]() 变为
变为![]() 。可以用赫尔德不等式来证明。闵可夫斯基不等式是Lp空间中的三角不等式,和赫尔德不等式一样,闵可夫斯基不等式取可数测度可以写成序列或向量的特殊形式。当n=3, p=2时,就是三维欧几里得空间中的三角不等式。
。可以用赫尔德不等式来证明。闵可夫斯基不等式是Lp空间中的三角不等式,和赫尔德不等式一样,闵可夫斯基不等式取可数测度可以写成序列或向量的特殊形式。当n=3, p=2时,就是三维欧几里得空间中的三角不等式。
(5.5)Jensen不等式:若f(x)在(a, b)上是下凸函数,![]() ,则有
,则有![]() ,琴生不等式可利用凸函数性质,通过归纳法证明。
,琴生不等式可利用凸函数性质,通过归纳法证明。![]() 几何平均
几何平均 ![]() 算术平均
算术平均 ![]() 平方平均。即
平方平均。即![\frac{1}{\frac{1}{x_{1}}+...+\frac{1}{x_{n}}}\leq \sqrt[n]{x_{1}...x_{n}}\leq \frac{x_{1}+...+x_{n}}{n}\leq \sqrt{\frac{{x_{1}}^{2}+...+{x_{n}}^{2}}{n}}](http://img.e-com-net.com/image/info8/b39083c90a2c4d549604f19424795c01.gif) 。可以用数学归纳法、琴生不等式、拉格朗日乘数法、排序不等式、柯西不等式等方法证明。
。可以用数学归纳法、琴生不等式、拉格朗日乘数法、排序不等式、柯西不等式等方法证明。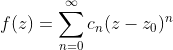 的和是定义在其收敛圆内的无穷可微函数,可以像实值函数一样求导,其k阶导数为
的和是定义在其收敛圆内的无穷可微函数,可以像实值函数一样求导,其k阶导数为![]() 在C中都有零点。(推论)任何复系数多项式
在C中都有零点。(推论)任何复系数多项式![]() 都可以表示成
都可以表示成 ![]() ,若不计次序,这种表示唯一。
,若不计次序,这种表示唯一。![]()
![]() ,可以用乘积函数求导法则
,可以用乘积函数求导法则 ![]() 两边积分来证明。
两边积分来证明。![]() ,且
,且![]() 可微。则根据复合函数微分法,有换元积分公式
可微。则根据复合函数微分法,有换元积分公式![]()
![]() 的形式,则求积分
的形式,则求积分![]() 可转化成求
可转化成求![]() ,求出后再把
,求出后再把![]() 代换回去。
代换回去。![]() ,其中
,其中![]() 有反函数,可导且导数不为0,则有换元积分公式
有反函数,可导且导数不为0,则有换元积分公式![]()
![]() 的积分,求出后再把
的积分,求出后再把 ![]() 代换回去。
代换回去。![]()
![]()
![]()
![]() ,它们都不是初等函数的复合,并且
,它们都不是初等函数的复合,并且![]()
![]() 是有理函数,其中
是有理函数,其中![]() 是多项式。任何有理函数Q(x)的原函数都可以由有理函数、超越函数lnx和arctanx表出,原函数的有理部分如果同分,应该有这样的公分母:它是多项式Q(X)分解出的全部因子的乘积,只是幂次比Q(x)中少1。
是多项式。任何有理函数Q(x)的原函数都可以由有理函数、超越函数lnx和arctanx表出,原函数的有理部分如果同分,应该有这样的公分母:它是多项式Q(X)分解出的全部因子的乘积,只是幂次比Q(x)中少1。![]() 型原函数:这里
型原函数:这里![]() 是u和v的有理函数,其中
是u和v的有理函数,其中![]() 和
和![]() 是单项式
是单项式![]() 的组合。可以作代换
的组合。可以作代换![]() ,利用万能公式,化为有理函数积分。而
,利用万能公式,化为有理函数积分。而![]() 或
或![]() 型积分,用t=tanx替换更方便。这些都是利用三角函数的特征做换元积分。
型积分,用t=tanx替换更方便。这些都是利用三角函数的特征做换元积分。![]() 型原函数:主要思路是找到替换
型原函数:主要思路是找到替换![]() ,且它们都是t有有理函数,就化为了有理函数的积分。
,且它们都是t有有理函数,就化为了有理函数的积分。![]() 型的积分也很重要,其中P(x)是次数n>2的多项式。Liouville曾证明这种积分一般不能用初等函数表示。当n=3,4时这种积分称为椭圆积分,n>4时称为超椭圆积分。椭圆积分经过初等变换、三角代换化为更简洁的形式,再查表获得值。
型的积分也很重要,其中P(x)是次数n>2的多项式。Liouville曾证明这种积分一般不能用初等函数表示。当n=3,4时这种积分称为椭圆积分,n>4时称为超椭圆积分。椭圆积分经过初等变换、三角代换化为更简洁的形式,再查表获得值。
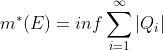 。这里
。这里![]() 是
是![]() 空间内的一个闭矩形点集(闭方体),其体积值
空间内的一个闭矩形点集(闭方体),其体积值![]() 是一个确定的非负数
是一个确定的非负数![]() 。矩形覆盖
。矩形覆盖![]() 是可列的。这相当于对一个点集E,从外部不断的去收缩,收缩到完全贴近为止的极限情况。这也是“外测度”名字的由来。注意不一定要求是闭方体的覆盖,也可以是其他类型的点集,甚至是开球这样的结构。一个集合的测度与它的划分方式无关。换句话说,构造一系列可列集合做覆盖时,可以将集合的体积规定的任意小,因为划分它并不影响集合本身的测度。
是可列的。这相当于对一个点集E,从外部不断的去收缩,收缩到完全贴近为止的极限情况。这也是“外测度”名字的由来。注意不一定要求是闭方体的覆盖,也可以是其他类型的点集,甚至是开球这样的结构。一个集合的测度与它的划分方式无关。换句话说,构造一系列可列集合做覆盖时,可以将集合的体积规定的任意小,因为划分它并不影响集合本身的测度。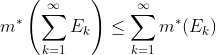 、平移不变性
、平移不变性![]() 。外测度不具有可加性。实际上无法对
。外测度不具有可加性。实际上无法对![]() 中的每个子集指定一个非负数,使得同时满足非负性/单调性/次可加性/平移不变性/可加性。这说明存在不可测集。对可测集还要增加更严格的条件。
中的每个子集指定一个非负数,使得同时满足非负性/单调性/次可加性/平移不变性/可加性。这说明存在不可测集。对可测集还要增加更严格的条件。![]() 取其区间长度b-a,高维矩形体的体积值取其各维区间长度的乘积值
取其区间长度b-a,高维矩形体的体积值取其各维区间长度的乘积值 ![]() 。测度是长度/面积/体积概念的推广。
。测度是长度/面积/体积概念的推广。![]() ,都存在一个盖住E的开集
,都存在一个盖住E的开集![]() ,使得
,使得 ![]() ,则E是勒贝格可测的。且定义其勒贝格测度为
,则E是勒贝格可测的。且定义其勒贝格测度为 ![]() 。测度为0的集合称为零测集。可测集全体记作
。测度为0的集合称为零测集。可测集全体记作![]() ,
,![]() 的元素称为不可测集。
的元素称为不可测集。![]() 中的开集或闭集都可测。因此可测集族M是空间
中的开集或闭集都可测。因此可测集族M是空间![]() 上的一个sigma代数。
上的一个sigma代数。![]() ,都存在一个能盖住E的可列开覆盖
,都存在一个能盖住E的可列开覆盖 ![]() ,使得
,使得 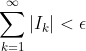 ,则集合E是勒贝格零测度集,即m(E)=0。
,则集合E是勒贝格零测度集,即m(E)=0。![]() ,即像点集的直径。函数在点处的振幅为邻域半径趋于0时的振幅极限,即
,即像点集的直径。函数在点处的振幅为邻域半径趋于0时的振幅极限,即![]() 。
。![]() ,划分的各个区间中最大的直径为划分P的长度
,划分的各个区间中最大的直径为划分P的长度![]() 。若在划分的每个区间
。若在划分的每个区间 ![]() 中取一个点
中取一个点![]() ,则
,则![]() 称为区间上一个取样划分。
称为区间上一个取样划分。![]() ,在该划分中再添加一些分割点和对应的取样点,得到一个新的划分
,在该划分中再添加一些分割点和对应的取样点,得到一个新的划分![]() ,称为原来划分的延拓。一个给定的划分可以一直延拓下去,直观上延拓后的划分比原来划分更精细,长度越来越小
,称为原来划分的延拓。一个给定的划分可以一直延拓下去,直观上延拓后的划分比原来划分更精细,长度越来越小 ![]() ,这相当于对所有取样划分定义了一个偏序关系。
,这相当于对所有取样划分定义了一个偏序关系。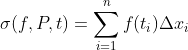 ,其中
,其中![]() 。
。![]() 趋于0时,黎曼和都收敛于同一个常数S,则称S为函数f在[a, b]上的黎曼积分,黎曼积分记为
趋于0时,黎曼和都收敛于同一个常数S,则称S为函数f在[a, b]上的黎曼积分,黎曼积分记为![]() ,都存在一个取样划分(P, t),使得对任何比它更精细的划分延拓
,都存在一个取样划分(P, t),使得对任何比它更精细的划分延拓![]() ,都有
,都有![]() ,则S为其黎曼积分。
,则S为其黎曼积分。![]() ,都存在
,都存在![]() ,使得对任何
,使得对任何![]() 的划分P,都有
的划分P,都有 ![\left | \sum_{i=1}^{n} \omega (f,[x_{i-1},x_{i}])(x_{i}-x_{i-1})\right |<\epsilon](http://img.e-com-net.com/image/info8/bd789c53d7144ba696d37e4b4d1adc5a.gif)
![]() ,使得
,使得 ![]() 。
。![]() ,使得
,使得 ![]() 的形式,c为常数。
的形式,c为常数。![]() ),且
),且 ![]()
![]() ,其中F(x)是f(x)的任一原函数。
,其中F(x)是f(x)的任一原函数。![]() 中,连续的参变函数 x=x(t), y=(y), z=z(t) 定义的映射
中,连续的参变函数 x=x(t), y=(y), z=z(t) 定义的映射 ![]() ,表示空间中的一条道路,其中 t 在闭区间[a, b]中变化。A=(x(a), y(a), z(a)), B=(x(b), y(b), z(b))为道路的起点和终点。如果起点和终点重合,则称道路是闭曲线。如果该映射是双射,则称为为简单道路或参数化曲线。如果映射函数T可微,且导函数连续,则称曲线是光滑的。对二维平面,则是平面上的曲线
,表示空间中的一条道路,其中 t 在闭区间[a, b]中变化。A=(x(a), y(a), z(a)), B=(x(b), y(b), z(b))为道路的起点和终点。如果起点和终点重合,则称道路是闭曲线。如果该映射是双射,则称为为简单道路或参数化曲线。如果映射函数T可微,且导函数连续,则称曲线是光滑的。对二维平面,则是平面上的曲线 ![]() ,平面曲线可以直接用函数y=f(x)表示。
,平面曲线可以直接用函数y=f(x)表示。![]() ,整个区域的面积
,整个区域的面积![]()
![]() ,体积为
,体积为![]() ,体积为
,体积为![]() ,曲线长度为
,曲线长度为![]()
![]() ,表面积为
,表面积为![]()
![]() 上可积,若极限
上可积,若极限 ![]() 存在,就称为f(x)在[a, t)上的反常积分。如果积分
存在,就称为f(x)在[a, t)上的反常积分。如果积分 ![]() 收敛,就称反常积分绝对收敛。
收敛,就称反常积分绝对收敛。![]() 收敛,当且仅当对任意的
收敛,当且仅当对任意的![]() ,都存在点
,都存在点![]() ,使得对一切大于c的
,使得对一切大于c的 ![]() ,都有
,都有 ![]() 。
。![]() 上,非负,递减,且在每个子区间上可积,则级数
上,非负,递减,且在每个子区间上可积,则级数 ![]() 和积分
和积分 ![]() 同时收敛或发散。
同时收敛或发散。![]() 收敛,只要下述两组条件有一组成立:积分
收敛,只要下述两组条件有一组成立:积分 ![]() 收敛且g(x)在[a, t)上单调有界;或者
收敛且g(x)在[a, t)上单调有界;或者 ![]() 在[a, t)上有界且g(x)当x趋于 t 时单调趋于0。
在[a, t)上有界且g(x)当x趋于 t 时单调趋于0。
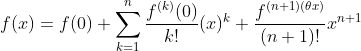
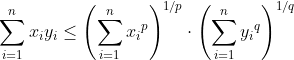
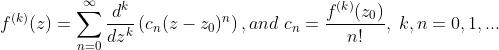
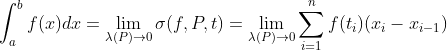
![\lim_{\lambda (P) \to 0}\sum_{i=1}^{n }\omega (f,[x_{i-1},x_{i}])(x_{i}-x_{i-1})=0](http://img.e-com-net.com/image/info8/0f1a19cad0bf4151a1bff22664520c0b.gif)