三维视觉论文阅读:DORN2018单目深度估计
论文
Deep Ordinal Regression Network for Monocular Depth Estimation
摘要
本篇论文认为之前基于encoder-decoer思路的方法虽然好看,但是不中用,不仅训练麻烦,深度图精度也就那样。本篇论文的方法独树一帜,即便是2020年来看,也是非常厉害。
但是就看文章的体验来说,真的把人看傻了。本人在理解思路时,完整看了代码进行辅助,链接如下:
https://github.com/dontLoveBugs/DORN_pytorch
网络模型
以下这个网络模型示意图,大概是我见过最含糊的图了吧;你好像看懂了,但是其实又根本啥也不知道,即不清楚网络结构参数,也不知道符号的具体意思。幸好有代码,不然真的要打人。
Dense Feature Extractor
特征提取器,这个可以用AlexNet,VGG或者ResNet,并没有严格限制。当然最好预训练,然后去掉全连接层。这篇论文推荐使用ResNet。
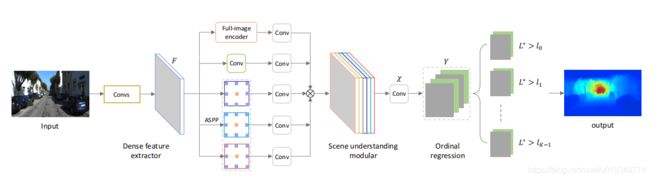
Scene Understangding Modular
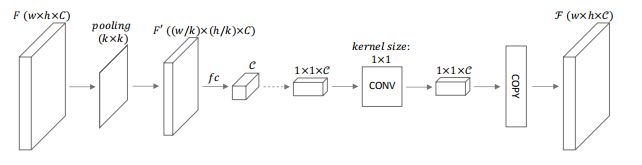
多尺度特征融合,完成对场景的全方位理解。这个地方为充分保证网络的感受野大小,分别用了一个带全链接层的Encoder(使用池化缩小范围,如下图所示)和4个大小不同的空洞卷积层;最后还有一堆1X1卷积对特征进行筛选。这个层有几个蜜汁操作,就是直接对特征图进行上采样,没有感觉出这种分辨率提高有什么价值~~。
不过一种可能时,深度离散化后,相邻像素的深度值很有可能就是同一个值,所以也许就算这样操作也没有问题。
Oridinal Regression
这个部分代码里一笔带过,文章里含含糊糊,真的不知道当时论文是哪方神圣review的,不知道他们是怎么看懂的。在讲这个模块之前,首先必须说一下这篇论文是怎们刻画深度的:
- 使用log空间表示深度,这个在Eigen2015里已经讲过,大家都很明白;
- 大部分论文把深度预测当作回归问题,但是这篇文章是当作分类问题,而且是有序分类。
那问题来了,什么是有序分类?
举个例子,假如在log空间里深度被分成 K = 5 K=5 K=5个。那么一个深度为 d = 3 d=3 d=3像素的深度值被预测 d ^ = 1 \hat{d}=1 d^=1和 d ^ = 4 \hat{d}=4 d^=4的差异其实是不一样的,因为 d ^ = 4 \hat{d}=4 d^=4距离 d = 3 d=3 d=3更近。
如果直接使用交叉熵做分类, d + 3 d+3 d+3和 d − 1 d-1 d−1都是错误预测,损失是一样的;这个原因想必大家都明白,因为交叉熵要用one-hot算,因为 d = 3 d=3 d=3对应 ( 0 , 0 , 1 , 0 , 0 ) (0,0,1,0,0) (0,0,1,0,0), d ^ = 1 \hat{d}=1 d^=1对应 ( 1 , 0 , 0 , 0 , 0 ) (1,0,0,0,0) (1,0,0,0,0), d ^ = 4 \hat{d}=4 d^=4对应 ( 0 , 0 , 0 , 1 , 0 ) (0,0,0,1,0) (0,0,0,1,0)。
本文作者注意到这个问题了,他稍微修改了一下这个表示规则,换成以下这种: d = 3 d=3 d=3对应 ( 1 , 1 , 1 , 0 , 0 ) (1,1,1,0,0) (1,1,1,0,0), d ^ = 1 \hat{d}=1 d^=1对应 ( 1 , 0 , 0 , 0 , 0 ) (1,0,0,0,0) (1,0,0,0,0), d ^ = 4 \hat{d}=4 d^=4对应 ( 1 , 1 , 1 , 1 , 0 ) (1,1,1,1,0) (1,1,1,1,0)。这样的话, d ^ + 3 \hat{d}+3 d^+3和 d ^ − 1 \hat{d}-1 d^−1的错误程度就不一样了。
讲完有序分类,说回论文里的操作。那显然现在也很简单了,如果深度被分成了 K K K个,那么每一个像素都需要在每一个深度值上进行二分类问题,即判断 K i = 0 K_i=0 Ki=0还是 K i = 1 K_i=1 Ki=1。代码里更简单,就是生成 ( b a t c h s i z e , 2 , K , H , W ) (batch size,2,K,H,W) (batchsize,2,K,H,W)维度的特征,然后直接进行 s o f t m a x softmax softmax分类;预测值大于0.5(由于softmax有两个输出结果,随便取一个就行,论文里第二个),就表示 K i = 1 K_i=1 Ki=1,反之就没有。
那问题来了,为啥用softmax预测的时候,又看不到有序性呢(每个$K_i$各自预测,互不相关)? 要回答这个问题,请看损失函数。
损失函数
这篇文章写的烂的第二个模块就是损失函数了,整了一大堆没啥用的东西,就是不说损失函数到底是个啥,搞人心态。
先贴一下损失函数,然后再解释(第一眼看到这个损失函数,我真的是一脸懵逼,倒不是因为符号很多,而是看不到怎们把预测值和GT进行比较,就比如a-b这种。
)。

首先简单解释公式,对于像素 ( w , h ) (w,h) (w,h)可以预测出其一个维度为 ( 1 , K ) (1,K) (1,K)的向量,向量的每个值都表示 P ( w , h ) ( K k = 1 ) P_{(w,h)}(K_k=1) P(w,h)(Kk=1)的概率,对应上图中的 P ( w , h ) k P^k_{(w,h)} P(w,h)k。举个例子,如果 K = 5 K=5 K=5, P ( w , h ) = ( 0.5 , 0.5 , 0.3 , 0.6 , 0.4 ) P_{(w,h)}=(0.5,0.5,0.3,0.6,0.4) P(w,h)=(0.5,0.5,0.3,0.6,0.4)。
l ( w , h ) l_{(w,h)} l(w,h)表示像素 ( w , h ) (w,h) (w,h)真实的深度值最大的 k k k,即 P ( K l ( w , h ) − 1 = 1 ) = 1 P(K_{l_{(w,h)}-1}=1)=1 P(Kl(w,h)−1=1)=1, P ( K l ( w , h ) = 1 ) = 1 P(K_{l_{(w,h)}}=1)=1 P(Kl(w,h)=1)=1, P ( K l ( w , h ) + 1 = 1 ) = 0 P(K_{l_{(w,h)}+1}=1)=0 P(Kl(w,h)+1=1)=0。看起来还是不像说人话,我举个例子。假如真实的深度值是 ( 1 , 1 , 1 , 0 , 0 ) , K = 5 (1,1,1,0,0),K=5 (1,1,1,0,0),K=5,那么 l ( w , h ) = 3 l_{(w,h)}=3 l(w,h)=3。
理解这两个东西,损失函数的计算也就非常简单了。
- 为啥损失函数没有出现类似 a − b a-b a−b的东西,原因是这个损失函数在设计是希望预测向量,小于 l ( w , h ) l_{(w,h)} l(w,h)的部分接近于0,大于等于 l ( w , h ) l_{(w,h)} l(w,h)的部分接近于1。这里用
log函数是因为其可以放大错误的部分,加速收敛。 - 为啥预测的时候不需要考虑有序关系,因为损失函数考虑了。
最后解释一下为啥大于等于$l_{(w,h)}$的部分接近于0,这个道理其实也很简单。我们将深度分成 K K K个格子,每个格子是一个范围值;但是深度值需要一个确定值,这应该怎么办呢?论文给出的答案也很简单,用当前格子的中心作为最终深度值。举个例子,深度分为 K = 5 K=5 K=5个格子,对应深度范围 ( 0 − 1 ] , ( 1 − 2 ] , ( 2 − 3 ] , ( 3 − 4 ] , ( 4 − 5 ] (0-1],(1-2],(2-3],(3-4],(4-5] (0−1],(1−2],(2−3],(3−4],(4−5],那么如果预测值为 ( 1 , 1 , 1 , 0 , 0 ) (1,1,1,0,0) (1,1,1,0,0),那么深度值就应该是 K 3 K_3 K3的上下边界的平均值,对应文章中的深度预测公式如下,其中 t 是 格 子 的 边 界 t是格子的边界 t是格子的边界。

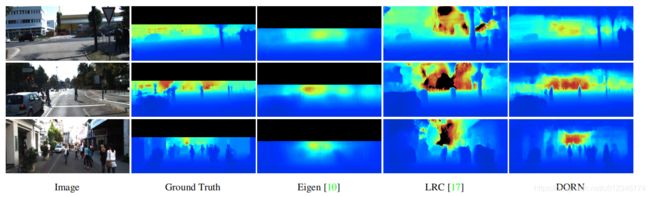
结果
其实不用考虑太多也知道本文的方法效果更好,原因从分类的角度来看就是:深度值直接回归,就是一个分类标签无限的分类任务;而给定大小的分类,则是一个有限的分类任务。网络参数就那么多,肯定是任务越简单越好。
但是真的是吐槽这个作者的行文风格,该说不说清楚,不需要讲的劈里啪啦说了一大堆。本次先总结着,因为心态爆炸,行文感觉也不一定好,以后再改改。