基于沙猫群优化算法的函数寻优算法

一、理论基础

1、沙猫群优化算法

文献[1]提出了一种新的元启发式算法，称为沙猫群优化算法(Sand Cat swarm optimization, SCSO)，该算法模拟了沙猫试图在自然界中生存的行为。

（1）初始化种群

在SCSO算法中，种群被称为沙猫群，每一个猫显示问题变量的值。该算法是一种基于种群的方法，将相关结构定义为向量。在$d$维优化问题中，沙猫是表示问题解的$1\times d$数组。每个变量值$(x_1,x_2,\cdots ,x_d)$都是一个浮点数。这里的每个$x$必须位于上下边界之间($\forall x\in [\text{lower},\text{upper}]$)。为了启动SCSO算法，首先根据问题的大小($N_{pop}\times N_d),(pop=1,2,\cdots ,n)$用沙猫种群创建一个候选矩阵。
此外，通过对定义的适应度函数进行评价，得到每只沙猫的适应度代价。此函数定义问题的相关参数，SCSO将获得参数(变量)的最佳值。将从每个沙猫个体输出相应函数的值。当一次迭代完成时，会选择到目前为止该迭代中适应度函数最优的沙猫，其他沙猫会在下一个迭代中尝试向这个最佳选择的猫移动。因为每次迭代中的最佳解决方案可以代表最接近猎物的猫。如果在下一次迭代中没有找到更好的解决方案，那么该迭代的解决方案就不会不必要地存储在内存中，这确保了内存的有效使用。

（2）搜索猎物(探索)

沙猫的猎物搜索机制依赖于低频噪声发射。每只沙猫的解表示为$X_i=(x_{i1},x_{i2},\cdots ,x_{id})$。SCSO算法得益于沙猫在低频探测方面的听觉能力，这样就声明了每只猫的敏感范围，沙猫可以感知低于2kHz的低频，在数学模型中，根据算法的工作原理，这个值($r_G$)将随着迭代过程的进行从2线性地降低为0，以逐渐靠近猎物而不会丢失或跳过。因此为了搜索猎物，假设沙猫的敏感范围为2kHz到0(式(1))，$S_M$​模拟了沙猫的听觉特性，其假设为2(当然对于不同问题可以适当调整以确定代理行为的速度)。值得一提的是，控制探索和利用之间转换的主要参数是$R$，其是根据式(2)获得的向量。此外，${\text{iter}}_{\text{c}}$是当前迭代次数，${\text{iter}}_{\max }$是最大迭代次数。$$r_G=S_M-\left(\frac{S_M\times {\text{iter}}_{\text{c}}}{{\text{iter}}_{\max }}\right)\text{\hspace{1em}(1)}$$$$R=2\times r_G\times \text{rand}(0,1)-r_G\text{\hspace{1em}(2)}$$$$r=r_G\times \text{rand}(0,1)\text{\hspace{1em}(3)}$$每个搜索代理(沙猫)根据最佳候选位置(${\text{Pos}}_{bc}$)和当前位置(${\text{Pos}}_c$)及其灵敏度范围($r$)更新自己的位置。因此，沙猫能够找到其他可能的最佳猎物位置(式(4))。该公式为算法在搜索区域找到新的局部最优提供了另一个机会。因此，获得的位置位于当前位置和猎物位置之间。此外，这是通过随机性实现的，而不是通过精确的方法。这样，算法中的搜索代理就有利于提高随机性。这使得算法操作成本低，复杂度高效。$$\text{Pos}(t+1)=r\cdot \left({\text{Pos}}_{bc}(t)-\text{rand}(0,1)\cdot {\text{Pos}}_c(t)\right)\text{\hspace{1em}(4)}$$

（3）攻击猎物(开发)

如前所述，沙猫根据听力检测猎物。为了数学建模SCSO的攻击猎物阶段，最佳位置(${\text{Pos}}_b$)(最佳解决方案)和当前位置(${\text{Pos}}_c$)由式(5)计算。此外，沙猫敏感范围假设为一个圆，这样，运动方向由随机角度决定($\theta$)在圆圈上。当然，在指定运动方向时，式(5)中声明的其他参数也是有效的。由于所选的随机角度介于0和360之间，其值将介于-1和1之间。这样，种群中的每个成员都能够在搜索空间的不同圆周方向上移动。SCSO有利于轮盘选择算法为每只沙猫选择一个随机角度。这样，沙猫就可以接近狩猎位置。随机角也用于避免局部最优陷阱。使用式(5)中的随机角度将对搜索代理的狩猎方式产生积极影响，并引导它们。${\text{Pos}}_{\text{rnd}}$表示随机位置，并确保相关猫可以靠近猎物。$$\begin{array}{c}{\text{Pos}}_{\text{rnd}}=\left|\text{rand}(0,1)\cdot {\text{Pos}}_b(t)-{\text{Pos}}_c(t)\right|\\ \text{Pos}(t+1)={\text{Pos}}_b(t)-r\cdot {\text{Pos}}_{\text{rnd}}\cdot \cos (\theta )\end{array}\text{\hspace{1em}(5)}$$

（4）探索和开发

参数$r_G$和$R$的自适应值确保了探索和开发。这些参数允许SCSO在两个阶段之间无缝切换。由于参数$R$取决于$r_G$，因此其波动范围也将减小。如前所述，当$r_G$的值均匀分布时，$R$值也是均匀的，因此根据问题，两阶段之间的操作机会是相当的。换句话说，$R$是区间$[-2r_G,2r_G]$中的一个随机值，其中$r_G$在迭代过程中线性地从2减少到0。当$R$的随机值为$[-1,1]$时，沙猫的下一个位置可以在其当前位置和狩猎位置之间的任何位置。当$R$小于或等于1时，SCSO算法迫使搜索代理开发，否则，搜索代理被迫探索和寻找猎物。在搜索猎物阶段(探索)，每只猫的不同半径避免了局部最优陷阱。这个特征也是攻击猎物(开发)的有效参数之一。式(6)为各沙猫在探索和开发阶段的位置更新情况。$$X_{t+1}=\{\begin{array}{l}{\text{Pos}}_b(t)-{\text{Pos}}_{\text{rnd}}\cdot \cos (theta)\cdot r|R|\le 1;exploitation\\ r\cdot \left({\text{Pos}}_{bc}(t)-\text{rand}(0,1)\cdot {\text{Pos}}_c(t)\right)|R|>1;exploration\end{array}\text{\hspace{1em}(6)}$$

（5）SCSO算法伪代码

SCSO算法伪代码如图1所示。

图1 SCSO算法伪代码

二、仿真实验与结果分析

将SCSO与PSO、BWO、GSA、WOA、GWO和SSA进行对比，以CEC2019的10个测试函数为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

函数：F1
PSO：最差值: 125.7827, 最优值: 19.6411, 平均值: 59.9356, 标准差: 26.2356
BWO：最差值: 0.00028033, 最优值: 4.5543e-17, 平均值: 1.3628e-05, 标准差: 5.2763e-05
GSA：最差值: 8.7194e-16, 最优值: 1.1227e-16, 平均值: 2.6264e-16, 标准差: 1.5211e-16
WOA：最差值: 1.3504e-70, 最优值: 1.5715e-85, 平均值: 4.513e-72, 标准差: 2.4653e-71
GWO：最差值: 1.3777e-26, 最优值: 3.3746e-29, 平均值: 1.9341e-27, 标准差: 3.3278e-27
SSA：最差值: 9.6455e-07, 最优值: 3.2465e-08, 平均值: 1.9702e-07, 标准差: 2.1445e-07
SCSO：最差值: 4.9989e-112, 最优值: 8.4894e-124, 平均值: 1.9095e-113, 标准差: 9.1099e-113
函数：F2
PSO：最差值: 16.4317, 最优值: 3.5316, 平均值: 7.2359, 标准差: 2.567
BWO：最差值: 0.0048713, 最优值: 1.0173e-12, 平均值: 0.00029057, 标准差: 0.0010193
GSA：最差值: 4.5926, 最优值: 5.0411e-08, 平均值: 0.50268, 标准差: 1.1475
WOA：最差值: 1.4167e-49, 最优值: 2.1639e-57, 平均值: 6.472e-51, 标准差: 2.6463e-50
GWO：最差值: 2.4568e-16, 最优值: 1.983e-17, 平均值: 9.2945e-17, 标准差: 6.0002e-17
SSA：最差值: 5.3701, 最优值: 0.24113, 平均值: 1.6728, 标准差: 1.1868
SCSO：最差值: 1.8099e-59, 最优值: 7.9364e-67, 平均值: 1.2948e-60, 标准差: 3.8732e-60
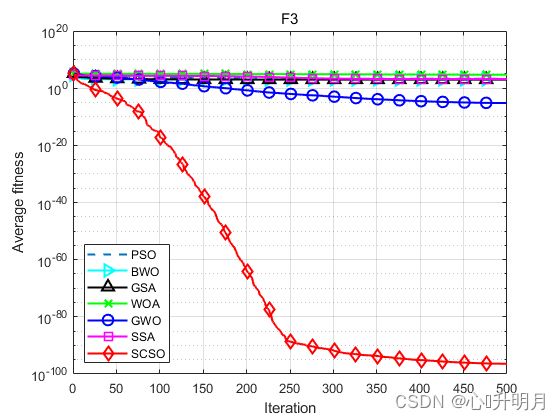
函数：F3
PSO：最差值: 6406.308, 最优值: 709.415, 平均值: 1877.1839, 标准差: 1307.9393
BWO：最差值: 1897.3074, 最优值: 470.3724, 平均值: 1098.3569, 标准差: 355.1772
GSA：最差值: 1708.573, 最优值: 421.7699, 平均值: 1016.1001, 标准差: 369.0638
WOA：最差值: 80939.4343, 最优值: 18230.1482, 平均值: 48500.6855, 标准差: 14018.3009
GWO：最差值: 3.6317e-05, 最优值: 5.0469e-08, 平均值: 6.3304e-06, 标准差: 9.1775e-06
SSA：最差值: 4068.8427, 最优值: 367.7928, 平均值: 1583.1015, 标准差: 907.8237
SCSO：最差值: 7.2776e-96, 最优值: 1.4695e-108, 平均值: 3.8826e-97, 标准差: 1.3846e-96
函数：F4
PSO：最差值: 20.8516, 最优值: 5.1927, 平均值: 14.2613, 标准差: 3.2652
BWO：最差值: 28.1311, 最优值: 5.2836, 平均值: 14.1761, 标准差: 6.3778
GSA：最差值: 10.7451, 最优值: 3.218, 平均值: 6.8793, 标准差: 1.8098
WOA：最差值: 91.445, 最优值: 4.302, 平均值: 56.1648, 标准差: 27.4234
GWO：最差值: 5.3693e-06, 最优值: 3.6414e-08, 平均值: 7.5008e-07, 标准差: 1.0986e-06
SSA：最差值: 18.06, 最优值: 5.7078, 平均值: 12.7243, 标准差: 3.1992
SCSO：最差值: 1.9253e-48, 最优值: 1.6991e-56, 平均值: 8.1861e-50, 标准差: 3.5476e-49
函数：F5
PSO：最差值: 6395.2917, 最优值: 404.4589, 平均值: 2530.1534, 标准差: 1565.2195
BWO：最差值: 72071.2165, 最优值: 130.0167, 平均值: 10228.12, 标准差: 19373.0062
GSA：最差值: 986.7163, 最优值: 26.4624, 平均值: 104.8854, 标准差: 198.0738
WOA：最差值: 28.7723, 最优值: 26.8601, 平均值: 28.1855, 标准差: 0.48047
GWO：最差值: 28.7582, 最优值: 25.6142, 平均值: 27.0459, 标准差: 0.69188
SSA：最差值: 17859.6297, 最优值: 25.7603, 平均值: 1045.14, 标准差: 3406.1233
SCSO：最差值: 28.8573, 最优值: 26.911, 平均值: 28.1894, 标准差: 0.71339
函数：F6
PSO：最差值: 163.0515, 最优值: 26.1644, 平均值: 69.0976, 标准差: 32.0217
BWO：最差值: 0.77032, 最优值: 1.1559e-17, 平均值: 0.025781, 标准差: 0.14062
GSA：最差值: 4.155e-16, 最优值: 1.3325e-16, 平均值: 2.4866e-16, 标准差: 7.7213e-17
WOA：最差值: 0.83709, 最优值: 0.041794, 平均值: 0.37122, 标准差: 0.20128
GWO：最差值: 1.5, 最优值: 0.24132, 平均值: 0.78576, 标准差: 0.36602
SSA：最差值: 3.2412e-06, 最优值: 4.2889e-08, 平均值: 2.832e-07, 标准差: 5.9079e-07
SCSO：最差值: 2.7767, 最优值: 1.0386, 平均值: 1.8505, 标准差: 0.4637
函数：F7
PSO：最差值: 0.18189, 最优值: 0.027113, 平均值: 0.081312, 标准差: 0.037168
BWO：最差值: 0.058094, 最优值: 0.0014321, 平均值: 0.0081523, 标准差: 0.012614
GSA：最差值: 5.4723, 最优值: 0.060644, 平均值: 0.40442, 标准差: 0.97922
WOA：最差值: 0.014203, 最优值: 5.3078e-05, 平均值: 0.0034635, 标准差: 0.0039636
GWO：最差值: 0.0052876, 最优值: 0.00069554, 平均值: 0.0020639, 标准差: 0.0010726
SSA：最差值: 0.40981, 最优值: 0.050968, 平均值: 0.18252, 标准差: 0.085388
SCSO：最差值: 0.00049949, 最优值: 6.3355e-06, 平均值: 0.00010341, 标准差: 0.00010399
函数：F8
PSO：最差值: -4276.493, 最优值: -8666.6644, 平均值: -6277.6633, 标准差: 1008.6792
BWO：最差值: -9088.7154, 最优值: -12289.1304, 平均值: -11128.4944, 标准差: 744.1347
GSA：最差值: -1733.0476, 最优值: -4138.4372, 平均值: -2619.5582, 标准差: 520.0808
WOA：最差值: -7159.7333, 最优值: -12567.448, 平均值: -10220.3663, 标准差: 1695.5833
GWO：最差值: -4266.5189, 最优值: -7263.8177, 平均值: -5933.7807, 标准差: 737.6522
SSA：最差值: -6019.9309, 最优值: -9236.5473, 平均值: -7698.2851, 标准差: 827.5151
SCSO：最差值: -4798.901, 最优值: -8102.1024, 平均值: -6746.3078, 标准差: 781.3359
函数：F9
PSO：最差值: 101.6671, 最优值: 33.772, 平均值: 63.186, 标准差: 14.5775
BWO：最差值: 0.026303, 最优值: 2.2737e-13, 平均值: 0.00099569, 标准差: 0.0047996
GSA：最差值: 53.7277, 最优值: 17.9093, 平均值: 35.8185, 标准差: 9.5504
WOA：最差值: 1.1369e-13, 最优值: 0, 平均值: 5.6843e-15, 标准差: 2.2884e-14
GWO：最差值: 27.3698, 最优值: 0, 平均值: 3.2067, 标准差: 6.4634
SSA：最差值: 80.5915, 最优值: 23.879, 平均值: 51.373, 标准差: 16.4352
SCSO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0
函数：F10
PSO：最差值: 5.9159, 最优值: 3.3858, 平均值: 4.7064, 标准差: 0.74564
BWO：最差值: 0.0064205, 最优值: 7.2316e-09, 平均值: 0.00049742, 标准差: 0.0013234
GSA：最差值: 1.5017, 最优值: 6.8364e-09, 平均值: 0.12823, 标准差: 0.37281
WOA：最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 4.0856e-15, 标准差: 2.3511e-15
GWO：最差值: 1.501e-13, 最优值: 7.5495e-14, 平均值: 1.0036e-13, 标准差: 1.5943e-14
SSA：最差值: 4.4244, 最优值: 5.1279e-05, 平均值: 2.67, 标准差: 0.88093
SCSO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0

实验结果表明：该算法在收敛速度和局部/全局最优解的寻优上均优于其他比较方法。

三、参考文献

[1] Amir Seyyedabbasi, Farzad Kian. Sand Cat swarm optimization: a nature-inspired algorithm to solve global optimization problems[J]. Engineering with Computers, 2022.