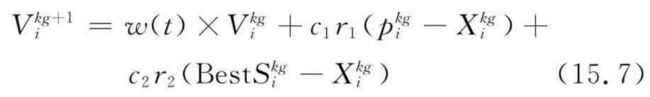粒子群优化算法求解函数最值
一、实验题目
计算如下二元函数的最小值:
(其中自变量x、y的范围均为[-50, 50])
![]()
- 用matlab代码实现。
- 代码必须能一键运行。
- 最后输出x,y和z的最优值及收敛到最优值所需的迭代步数。
- 算法关键参数需要注释清楚(如权重因子、学习因子、速度变化范围等)。
二、算法原理
粒子群优化算法求最优解
1、问题描述
D维空间中,有N个粒子;
粒子i位置:xi=(xi1,xi2,…xiD),将xi代入适应函数f(xi)求适应值;
粒子i速度:vi=(vi1,vi2,…viD)
粒子i个体经历过的最好位置:pbesti=(pi1,pi2,…piD)
种群所经历过的最好位置:gbest=(g1,g2,…gD)
通常,在第d(1≤d≤D)维的位置变化范围限定在![]() 内,速度变化范围限定在
内,速度变化范围限定在![]() 内(即在迭代中若
内(即在迭代中若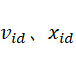 超出了边界值,则该维的速度或位置被限制为该维最大速度或边界位置)
超出了边界值,则该维的速度或位置被限制为该维最大速度或边界位置)
2、算法公式
粒子i的第d维速度更新公式:
![]()
粒子i的第d维位置更新公式:
![]()
![]() —第k次迭代粒子i飞行速度矢量的第d维分量
—第k次迭代粒子i飞行速度矢量的第d维分量
![]() —第k次迭代粒子i位置矢量的第d维分量
—第k次迭代粒子i位置矢量的第d维分量
c1,c2—加速度常数,调节学习最大步长
r1,r2—两个随机函数,取值范围[0,1],以增加搜索随机性
w —惯性权重,非负数,调节对解空间的搜索范围
粒子速度更新公式包含三部分:
第一部分为粒子先前的速度
第二部分为“认知”部分,表示粒子本身的思考,可理解为粒子i当前位置与自己最好位置之间的距离。
第三部分为“社会”部分,表示粒子间的信息共享与合作,可理解为粒子i当前位置与群体最好位置之间的距离。
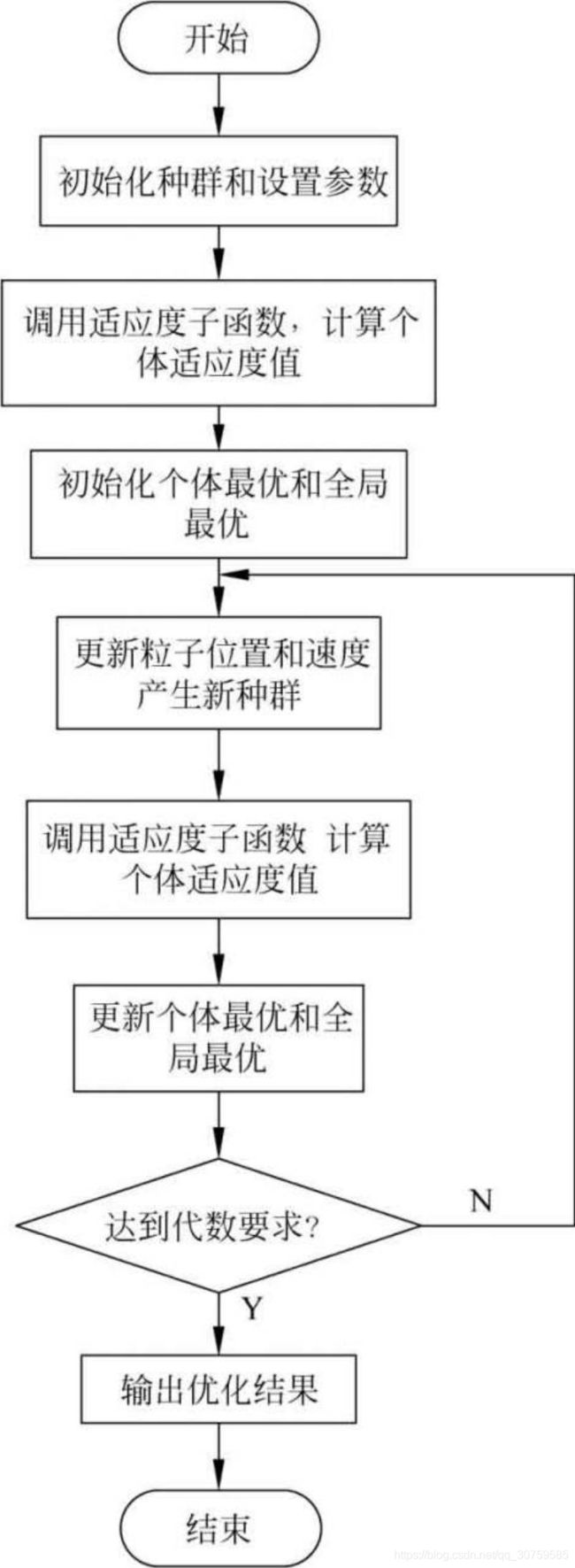
3、算法流程
(1)Initial:
初始化粒子群体(群体规模为n),包括随机位置和速度。
设定参数运动范围,设定学习因子c1、c2,最大进化代数G,kg表示当前的进化代数。在一个D维参数的搜索解空间中,粒子组成的种群规模大小为Size,每个粒子代表解空间的一个候选解,其中第i(1≤i≤Size)个粒子在整个解空间的位置表示为Xi,速度表示为Vi。第i个粒子从初始到当前迭代次数搜索产生的最优解,个体极值Pi,整个种群目前的最优解为BestS。随机产生Size个粒子,随机产生初始种群的位置矩阵和速度矩阵。
(2)Evaluation:
根据fitness function ,评价每个粒子的适应度。
个体评价(适应度评价):将各个粒子初始位置作为个体极值,计算群体中各个粒子的初始适应值f(Xi),并求出种群最优位置。
(3)Update the speed and position:
更新粒子的速度和位置,产生新种群,并对粒子的速度和位置进行越界检查,为避免算法陷入局部最优解,加入一个局部自适应变异算子进行调整。
其中,kg=1,2,…,G,i=1,2,…,Size,r1和r2为0到1的随机数,c1为局部学习因子,c2为全局学习因子,一般取c2大些。
(4)Find the Pbest:
对每个粒子,将其当前适应值与其个体历史最佳位置(pbest)对应的适应值做比较,如果当前的适应值更高,则将用当前位置更新历史最佳位置pbest。
(5)Find the Gbest:
对每个粒子,将其当前适应值与全局最佳位置(gbest)对应的适应值做比较,如果当前的适应值更高,则将用当前粒子的位置更新全局最佳位置gbest。
(6)Update the Velocity:
根据公式更新每个粒子的速度与位置。如未满足结束条件,则返回步骤2。通常算法达到最大迭代次数 或者最佳适应度值的增量小于某个给定的阈值时算法停止。
三、实验代码与结果
1、实验代码
function main
%由于原代码求取的最大值,最小值的话直接将目标函数取成相反数即可
%很显然,结果只能无限逼近 3与5 跟算法原理有关(类似遗传算法)
clear all;
close all;
%(1)初始化粒子群算法参数
min=-50;max=50;%粒子位置范围
Vmax=25;Vmin=-25;%粒子运动速度范围
c1=1.3;c2=1.7; %学习因子[0,4]
wmin=0.20;wmax=0.90;%惯性权重
G=400; % 最大迭代次数
Size=100; %初始化群体个体数目
for i=1:G
w(i)=wmax-((wmax-wmin)/G)*i; %随着优化进行,应降低自身权重
end
for i=1:Size
for j=1:2
x(i,j)=min+(max-min)*rand(1); %随机初始化位置
v(i,j)=Vmin +(Vmax-Vmin)*rand(1); %随机初始化速度
end
end
%(2)计算各个粒子的适应度,并初始化Pi、plocal和最优个体BestS
for i=1:Size
p(i)=func(x(i,:));
y(i,:)=x(i,:);
if i==1
plocal(i,:)=evaluate_localbest(x(Size,:),x(i,:),x(i+1,:));
elseif i==Size
plocal(i,:)=evaluate_localbest(x(i-1,:),x(i,:),x(1,:));
else
plocal(i,:)=evaluate_localbest(x(i-1,:),x(i,:),x(i+1,:));
end
end
BestS=x(1,:);%初始化最优个体BestS
for i=2:Size
if func(x(i,:))>func(BestS)
BestS=x(i,:);
end
end
%(3)进入主循环
for kg=1:G
for i=1:Size
M=1;
if M==1
v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(plocal(i,:)-x(i,:));%局部寻优:加权,实现速度的更新
elseif M==2
v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(BestS-x(i,:)); %全局寻优:加权,实现速度的更新
end
for j=1:2 %检查速度是否越界
if v(i,j)Vmax
v(i,j)=Vmax;
end
end
x(i,:)=x(i,:)+v(i,:)*1; %实现位置的更新
for j=1:2 %检查位置是否越界
if x(i,j)max
x(i,j)=max;
end
end
%自适应变异,避免粒子群算法陷入局部最优
if rand>0.60
k=ceil(2*rand);
x(i,k)=min+(max-min)*rand(1);
end
%(4)判断和更新
if i==1
plocal(i,:)=evaluate_localbest(x(Size,:),x(i,:),x(i+1,:));
elseif i==Size
plocal(i,:)=evaluate_localbest(x(i-1,:),x(i,:),x(1,:));
else
plocal(i,:)=evaluate_localbest(x(i-1,:),x(i,:),x(i+1,:));
end
if func(x(i,:))>p(i) %判断当此时的位置是否为最优的情况,当不满足时继续更新
p(i)=func(x(i,:));
y(i,:)=x(i,:);
end
if p(i)>func(BestS)
BestS=y(i,:);
end
end
Best_value(kg)=func(BestS);
end
figure(1);
kg=1:G;
plot(kg,-Best_value,'r','linewidth',2);
xlabel('generations');ylabel('Fitness function');
% display('Best Sample=');disp(BestS);
display('X=');disp(BestS(1));
display('Y=');disp(BestS(2));
% display('Biggest value=');disp(Best_value(G));
display('Z=');disp(Best_value(G));
for i=1:G
if Best_value(i)==Best_value(end)
disp('收敛到最优值需要的迭代步数');
disp(i);
break;
end
end
end
function f = func(x)
f=-(0.5*(x(1)-3)^2+0.2*(x(2)-5)^2-0.1);
end
function f =evaluate_localbest(x1,x2,x3)%求解粒子环形邻域中的局部最优个体
K0=[x1;x2;x3];
K1=[func(x1),func(x2),func(x3)];
[maxvalue index]=max(K1);
plocalbest=K0(index,:);
f=plocalbest;
end 2、实验结果
X=
3.0022
Y=
5.0068
Z=
0.1000
收敛到最优值需要的迭代步数
379
PS:该代码有智能控制刘金锟第四版更改,更加详细的内容请查看原作。