文献翻译__基于自适应全变差L1正则化的椒盐图像去噪
文章下载–我的Gitee
Adaptive total variation L1 regularization for salt and pepper imagedenoising
ABSTRACT
In this article, we propose an adaptive total variation (TV) regularization model for salt and pepper denoising in digital images. The adaptive TV denoising method is developed based on the general regularized image restoration model with L1 fidelity for handling salt and pepper noise model. An estimation for regularization parameter is also proposed based on the characteristics
of the salt and pepper noise. We implement the proposed adaptive TV-L1 regularization model efficiently for image denoising using the primal dual gradient method. In the experiments, the full-reference image quality assessment metrics are used for evaluating denoising quality across various noise levels in different synthetic and real images. The denoising results are compared to other similar salt and pepper image denoising methods and our results indicate we obtain artifact free edge preserving restorations.
Keywords:Image denoising,Salt and pepper noise,Total variation,Image restoration,Primal dual gradient,Adaptive image denoising,Image quality assessment
基于自适应全变差L1正则化的椒盐图像去噪
本文提出了一种用于数字图像中椒盐去噪的自适应总变分正则化模型。针对椒盐噪声模型,提出了一种基于L1保真度的一般正则化图像恢复模型的自适应图像去噪方法。根据椒盐噪声的特点,提出了一种正则化参数估计方法。我们使用原始对偶梯度法有效地实现了自适应TV-L1正则化模型的图像去噪。在实验中,使用全参考图像质量评价指标对不同噪声水平下的不同合成图像和真实图像的去噪质量进行了评价。将去噪结果与其他类似的盐和胡椒图像去噪方法进行了比较,结果表明我们得到了无伪影的边缘保持复原。
关键词:图像去噪,椒盐噪声,全变差图像恢复,原始对偶梯度,自适应图像去噪,图像质量评价
1.介绍
图像复原[1-6]是图像处理中常见的问题。真实图像通常受到许多因素的破坏,如噪声、灰尘、划痕等。失真降低了其他图像处理任务的有效性,如图像分割[7]和模式识别[8]。因此,图像恢复对提高图像质量起着至关重要的作用。图像去噪是图像复原中最重要的问题之一。噪声通常出现在各种成像系统拍摄的数字图像中,如数码相机、CT/X-射线/MRI扫描仪、显微镜、望远镜等。有一些常见的类型的噪声:高斯噪声[9]、泊松噪声[10]、脉冲噪声[11,12]和混合高斯-泊松噪声[13]。椒盐(SNP)噪声是脉冲噪声的一种简单类型[14]。SNP噪声可以由图像信号[14]中的尖锐和突然的干扰引起。SNP噪波只有两个灰度值:白色像素(最大灰度值)和黑色像素(最小灰度值)。白色像素也称为盐像素,黑色像素称为胡椒像素。
为了消除SNP噪声,使用了许多方法。在本文中,我们只关注不基于机器学习的方法。它们包括正则化、非线性滤波器、小波分析、数学变换和主要成分分析(PCA)。对于非线性滤波,中值滤波是处理SNP噪声的有效方法。经典的中值滤波(MF)是在Lim[15]的工作中提出的。然而,MF仅对低密度SNP噪声有效。对于中密度和高密度噪声,MF不能完全去除噪声,通常会产生许多缺陷。为了消除这一缺陷,提出了自适应中值滤波(AMF)[16]和自适应中心加权中值滤波(ACWMF)[17]。AMF和ACWMF虽然比中频更有效,但在中密度和高密度噪声情况下仍然存在许多缺陷。近年来,Erkan等人提出了基于像素密度滤波(BPDF)的方法。[12]是一种有效的SNP噪声过滤器。然而,对于高密度噪声的情况,BPDF通常会产生破坏图像结构的雨滴效果。否则,BPDF无法在包含接近噪波灰度值的灰度值的图像区域上有效工作(即,对于8位灰度级图像,灰度值通常为0到10或250到255)。
https://doi.org/10.1016/j.ijleo.2019.163677,2019年7月30日收到;2019年10月8日收到;2019年10月26日接受⁎通讯员。
电子邮件地址:than [email protected],than [email protected](D.N.H.Thanh),than [email protected](L.T.Thanh),[email protected](N.N.Hien),[email protected](S.Prasath)。
Optik-国际光与电子光学杂志208(2020)163677 0030-4026/©2019Elsevier GmbH.。版权所有。
维纳滤波[15]是另一种用于处理SNP噪声的众所周知的非线性滤波器。然而,维纳滤波只能去除低密度的SNP噪声。对于中密度和高密度噪声,维纳滤波效果不佳,通常情况下噪声仍然存在。因此,有一些自适应维纳滤波器被提出来提高降噪性能[18,19]。双边滤波器[20]是主要为去除高斯噪声而设计的非线性滤波器。为了去除脉冲噪声和SNP噪声,提出了一种自适应双边滤波(ABF)[21]。ABF在低密度和中密度SNP噪声上工作良好。
另一类SNP去噪方法是基于小波分析的。噪声可以通过各种方法去除,如经验贝叶斯[22]、错误发现率[23]、Stein的无偏风险估计[24]、极小极大估计[25]或通用阈值[25]。该方法可以在各种小波域上实现,如Haar、Coiflet、Symlet等。正则化是一种新的方法,近年来取得了许多成果。正则化对去除高斯噪声、泊松噪声和高斯-泊松噪声特别有效。已有一些工作将正则化方法应用于脉冲噪声,包括SNP噪声。赫曼特等人。提出的广义综合和分析先验算法[11] (GSAP)。Aggarwal等人。[26]提出了一种基于空间光谱图像正则化(SSTV)的脉冲噪声去除模型。SSTV可用于去除高斯噪声或单独的脉冲噪声以及组合的高斯-脉冲噪声。Chan和Esedoglu在[27]中提出了一种基于L1范数全变差的SNP去噪方法(TVL1)。尽管TVL1方法对SNP噪声是有效的,但相应的正则化参数估计仍然是一个开放的问题。
在本文中,我们的贡献主要集中在:重新建立了基于一阶全变分的SNP噪声去噪模型;考虑了一般图像恢复问题,建立了显式SNP去噪模型;提出了一种基于正则化参数的SNP噪声特征估计方法;提出了一种基于原始对偶梯度法的显式模型求解算法[28,29]。我们的方法是一种新的L1范数自适应全变分模型,其中自适应正则化参数是基于受污染像素的平均值来计算的,从而有效地指导保持边缘的全变分来降低SNP噪声。(椒盐噪声)
在实验中,我们在合成图像和加州大学伯克利分校数据集的真实自然图像上测试了所提出的去噪方法[30]。去噪质量基于全参考图像质量评价指标:峰值信噪比(PSNR)和结构相似性(SSIM)。我们将该模型的去噪结果与现有的代表不同领域的方法进行了比较:中值滤波(MF、ACWMF、BPDF)、维纳滤波(Wiener)、自适应双边滤波(ABF)、基于FDR和Coiflet的小波去噪方法(Wavelet)、基于正则化的模型(GSAP、TVL1和SSTV)。在合成图像和真实图像上的实验结果表明,我们在不同的SNP噪声水平上获得了直观和定量的高质量结果。
本文的其余部分安排如下。第二节提出了基于TV-L1的自适应SNP去噪模型,并给出了正则化参数估计。第三节给出了实验结果,并与相关图像去噪方法进行了直观和定量的比较。最后,第四节对文章进行了总结。
2.基于自适应全变差L1正则化的椒盐去噪
2.1 图像复原问题与全变分
设 u ( x ) , v ( x ) ∈ R u(x),v(x) \in R u(x),v(x)∈R分别是灰度恢复图像和灰度损坏(噪声)图像,其中 x = ( x 1 , . . . , x n ) ∈ Ω ⊂ R h x=(x_1,...,x_n) \in \Omega \subset R^h x=(x1,...,xn)∈Ω⊂Rh是像素位置, Ω \Omega Ω是图像域。灰度图像的全变差[31,13]图像复原问题具有如下形式:
其中 ∣ ∣ p ||_p ∣∣p是 L p L^p Lp-范数, E ( ) E() E()是能量泛函, K K K是过滤算子, λ \lambda λ是正则化参数。
我们注意到,彩色图像可以被认为是各种灰度通道的组合。因此,该模型适用于彩色图像。此外,为了简化与其他相关SNP去噪模型的表示和评估,我们这里只考虑2D图像的情况,即 h = 2 , x = ( x 1 , x 2 ) h = 2, x=(x_1,x_2) h=2,x=(x1,x2)。对于彩色图像,可以用类似的方式写出模型。在p=2的情况下,模型(1)用于被高斯噪声污染的图像的有效恢复。如果p=1,则模型(2)对SNP去噪是有效的。
根据恢复的类型,过滤算子 K K K具有各种形式。对于图像去卷积问题, K K K可以是卷积核,例如高斯核。对于文中所考虑的去噪问题,算子 K K K是单位算子 I I I,即 K I KI KI。
对于能量泛函 E ( u ) E(u) E(u)的项,我们有以下几种重要的类型:
- 一阶总变差[32]:
- 非局部总变异[33]:
其中 y = ( y 1 , . . . , y n ) ∈ Ω ; w ( x , y ) y = (y_1,...,y_n)\in \Omega;w(x,y) y=(y1,...,yn)∈Ω;w(x,y)用于测量以像素 x x x和 y y y为中心的面片的相似性的非局部权重。
- 高阶总变差[34]:
![]()
- 分数阶总变差[35]:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UeFWzDzr-1658552558493)(C:%5CUsers%5CAdministrator%5CAppData%5CRoaming%5CTypora%5Ctypora-user-images%5Cimage-20220707094808492.png)]
- Mumford-Shah [5]:
![]()
其中 Γ \Gamma Γ是边缘像素集, H 1 H1 H1 是1D Hausdorff 度量,参数 k k k > 0。
- 欧拉弹性[36]:
其中 a,b > 0。
用一阶全变分(2)去噪可能会产生伪影。其他类型(3)-(7)可以避免这一缺陷。然而,在从复杂结构的噪声(如高斯噪声或泊松噪声)中恢复图像时,通常会出现伪影。
2.2 基于自适应TV-L1正则化的椒盐去噪算法
图像上的SNP噪声具有以下形式[2]:
值 δ m a x \delta_{max} δmax是盐像素(白色像素)的灰度值,而值 δ m i n \delta_{min} δmin是胡椒像素(黑像素)的灰度值。对于8位灰度图像, δ m i n \delta_{min} δmin=0,$\delta_{max} 255 分钟。总和 255分钟。总和 255分钟。总和q =q_1+q_2$称为噪声水平。
如上所述,选择能量函数 E ( u ) E(u) E(u)可以避免伪影。然而,对于SNP噪声,去噪结果中很少出现伪影。因此,在本文中,我们只考虑能量函数为一阶全变分的情况。
另一方面,模型(1)是解决图像恢复问题的一般形式。对于SNP去噪问题,噪声图像的像素可以分为:不变像素(无噪声像素)、盐像素和胡椒像素以及算子 K = I K=I K=I。因此,数据保真项的积分下的表达式(即,模型(1)中的第二项)可以重写如下:
- 如果p=1,我们可以很容易地重写(8)如下:
- 如果p>=2,则表达式(8)等同于以下公式:
从(9)和(10)可以看出,对于SNP去噪问题,值p=1比p>=2的情况更简单,因为模型(1)对应的欧拉-拉格朗日方程不包含数据保真项(取u的导数后,这一问题是恒定的)。因此,SNP去噪问题的模型(1)可以重写如下:
对于总变异范数,我们有两种类型:
- 各向异性总变化:
- 各向同性总变化:
许多去噪工作表明,各向同性全变分比各向异性全变分更有效。因此,在本文中,我们只考虑各向同性全变分。
由此,基于全变差的显式SNP去噪模型可以表示为:
选择合适的正则化参数可以提高去噪质量。正则化参数将根据SNP噪声的特性进行估计。
2.3 自适应正则化参数估计
对于自然图像,像素的灰度值通常不会达到边界值 δ m a x \delta_{max} δmax, δ m i n \delta_{min} δmin。因此,如果像素的灰度值等于边界值,则可以将其视为噪声像素。特别是对于高密度的SNP噪声,其表述更为准确。在实际自然图像去噪的情况下,我们提出了一种估计正则化参数 λ \lambda λ的方法如下:
其中, u v u_v uv是噪声图像 v v v在区间[0,1]内归一化的损坏像素值的平均值, ψ η \psi_{\eta} ψη是盐和胡椒噪声水平。
设 I , I c , I m a x , I m i n I,I_c,I_{max},I_{min} I,Ic,Imax,Imin分别是一幅图像的所有象素的集合、一组被破坏的象素、一组具有灰度值最大的象素 δ m a x \delta_{max} δmax、一组具有灰度值最小的象素 δ m i n \delta_{min} δmin。在SNP噪声的情况下,我们认为这 I c = I m a x ⋃ I m i n I_c = I_{max}\bigcup I_{min} Ic=Imax⋃Imin。对于具有高密度噪声的有噪声的自然图像,平均 u v u_v uv和噪声水平q可以如下评估:
其中, v I c v_{I_c} vIc是 I c I_c Ic中像素的灰度值, c a r d ( ) card() card()是集合基数(集合的元素数量)。
2.4 原始对偶梯度法在椒盐去噪中的应用
我们考虑离散形式的优化问题(12)如下:
其中
问题(14)可以改写为最小-最大问题:
![]()
其中![]()
Div是散度算符,<,>是标量积, ( i , j ) ∈ { 1 , . . . , n } × { 1 , . . . , m } (i,j) \in \{1,...,n\}\times\{1,...,m\} (i,j)∈{1,...,n}×{1,...,m}。
问题(15)包含两个变量 u u u和p。
- 首先,我们通过固定对偶变量p来解决 u u u的优化问题。最优条件是:
我们可以用梯度下降法求解(16):
- 其次,我们解决了给定u的对偶变量p的优化问题。最优条件是:
其中 ∂ ∂ ∂表示次梯度,并且
我们使用投影梯度法求解(17):
其中 ρ > 0 \rho > 0 ρ>0。
我们可以用初始条件 u [ 0 ] = v u^{[0]}=v u[0]=v,p [ 0 ] ^{[0]} [0]=0计算 u [ k + 1 ] u^{[k+1]} u[k+1],p [ k + 1 ] ^{[k+1]} [k+1]。对于停止条件,我们可以使用迭代次数 k>K 或容差 ∣ u [ k + 1 ] − u [ k ] ∣ < = ε |u^{[k+1]}-u^{[k]}|<=\varepsilon ∣u[k+1]−u[k]∣<=ε。算法 1 中介绍了针对 SnP 图像去噪所提出的自适应 TV L$^1 $正则化的详细信息。
| 算法 1. 用于椒盐图像去噪的自适应总变分 L 1 ^1 1 正则化 (ATVL1) |
|---|
 |
3.实验结果与讨论
我们在 MATLAB 上处理了所提出的 SNP 去噪方法的实验。计算系统配置为 Windows 10 Pro,Intel Core i5,1.6 GHz,4GB 2295 MHz DDR3 RAM 内存。我们将提出的基于自适应 TV-L1 的模型及其基于原始双梯度的实现的参数配置如下: ε = α = 1 0 − 5 , τ = 0.02 , ρ = 6.25 \varepsilon=\alpha=10^{-5},\tau=0.02,\rho=6.25 ε=α=10−5,τ=0.02,ρ=6.25此外,我们将最大迭代次数限制为 K=500。
3.1 图像质量评估
为了评估去噪质量,我们使用完整的参考图像质量指标:峰值信噪比 (PSNR) 和结构相似度 (SSIM)。这些指标广泛用于图像处理文献[13,37–40]。
PSNR [40] 定义如下:
![]() 其中是均方误差, u 0 u_0 u0 是原始图像(真实值), u m a x u_{max} umax 表示最大灰度值, m × n m\times n m×n 是图像大小,例如对于 8 位图像 u m a x u_{max} umax=255 。请注意,较高的 PSNR(以分贝 - dB 为单位)表示图像质量更好。
其中是均方误差, u 0 u_0 u0 是原始图像(真实值), u m a x u_{max} umax 表示最大灰度值, m × n m\times n m×n 是图像大小,例如对于 8 位图像 u m a x u_{max} umax=255 。请注意,较高的 PSNR(以分贝 - dB 为单位)表示图像质量更好。
结构相似度(SSIM)[40] 是一种比 PSNR 更好的图像质量比较误差度量,SSIM 值在 [0,1] 范围内,值接近 1 表示结构保存更好。 SSIM 在两个图像 , w 1 , w 2 w_1,w_2 w1,w2 之间计算,它们的大小相同,为 m×n:
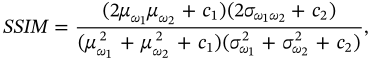
其中 $µ_{w_i} 是 是 是w_i 的平均值, 的平均值, 的平均值,\sigma_{w_i}^2 是 是 是w_i 的方差,协方差 的方差,协方差 的方差,协方差\sigma_{w_1w_2} 和稳定参数 和稳定参数 和稳定参数c_1,c_2 。 S S I M 中的参数设置为 [ 40 ] 中的默认值如下: 。 SSIM 中的参数设置为 [40] 中的默认值如下: 。SSIM中的参数设置为[40]中的默认值如下:c_1=(K_2L)^2,K_1=0.01,K_2=0.03 ,和 ,和 ,和L=255$对于 8 位图像。对于图像去噪,在添加合成噪声的情况下,将原始无噪声图像和恢复图像进行比较,以找出恢复方法在去除噪声的同时保留了多少结构。
3.2 图像数据集和测试用例
我们考虑两个测试用例:对生成的合成图像和 UC-Berkeley 数据集 [30] 的真实自然图像进行去噪。
第一个测试用例:对生成的图像进行去噪。我们创建了一个合成图像 T01,如图 1 所示,黑色背景(灰度值为 0)包含一个白色圆盘(灰度值为 255)、一个白色三角形(灰度值为 255)和一个白色矩形(灰度值为灰度值为 255)包围一个黑色磁盘(灰度值为 0)。图像尺寸为 256×256 像素。形状边缘像素的灰度值约为 250-255。
 |
|---|
| 图 1. 生成的 ID 为 T01 的图像。 |
我们在原始图像中添加噪声水平为 40% 和 60% 的 SNP 噪声。 40%噪声级去噪结果见图2,60%噪声级去噪结果见图3。
对于 40 % 的噪音水平,维纳滤波器无效。仍然有很多噪音。因为图像仅包含相似的灰度值(0 和 255),所以 BPDF 失败。它破坏了所有图像结构。 MF 和 ACWMF 很好地去除了噪音,但它们造成了一些缺陷。 MF和ACWMF的去噪结果差异很小。小波去噪方法可以很好地去除噪声,但会产生很多伪影。否则,形状的边缘会变得太模糊。 GSAP 方法有效地去除了噪声,但形状的边缘没有得到很好的保留。边缘有些模糊。 ABF 的结果中仍然存在噪声,并且各种形状的边缘没有得到很好的保留。 SSTV 模型获得了类似的边缘伪影以及与 TV 正则化相关的阶梯。
TVL1和所提方法的去噪效果最好。我们的方法稍微好一点,但很难通过直观地查看结果来区分。出于这个原因,我们为每个比较模型提供了相应的最佳 PSNR (dB) 和 SSIM 值,并且所提出的方法在两个误差度量中都获得了最高(即最佳去噪结果)值。
噪音水平为60%。维纳滤波器,BPDF,MF,ACWMF,小波去噪方法和GSAP的去噪结果与40%噪声的情况类似。从各种形状内的均匀区域可以看出,ABF不能完全去除噪声,并且也不能保留边缘。SSTV模型具有强烈的楼梯伪影和边缘涂抹。用我们的方法和TVL1去噪结果是最好的。在这种情况下,我们的方法比TVL1更好地保留边缘:在三角形的顶角上清晰可见。此外,PSNR和SSIM值表明我们的方法的去噪结果是最好的。
第二个测试用例:对 UC-Berkeley 数据集的真实自然图像进行去噪。数据集包含以 JPEG 格式存储的真实图像。我们选择了 20 张如图 4 所示的图像来进行测试。
 |
|---|
| 图 4. 从 UC-Berkeley 数据集 (BSDS) 中选择的图像及其 ID。 |
图 5 显示了各种噪声水平的去噪结果:ID 为 157055 的“男人和女人”图像的 20 %、40 %、50 %、60 %、70 % 和 80 %。我们可以看到,噪声水平高达50 %,图像的所有细节都保留得很好。对于更高的噪声水平,一些小细节会丢失,但会保留人体形状。对于非常高的噪声密度(例如 80%),去噪结果是可以接受的(PSNR = 19.2858,SSIM = 0.49292)。虽然丢失了很多细节,但我们仍然可以辨认出还原图像中男人和女人的轮廓。
 |
|---|
| 图 5. 提出的自适应 TV-L1 方法对来自 BSDS 的 ID 为 157,055 的“男人和女人”图像的各种噪声水平的去噪结果 |
图 6 给出了 MF、ACWMF、Wiener 滤波器、小波去噪方法、GSAP、BPDF、TVL1、ABF、SSTV 等方法与所提出的方法在 60% 的噪声水平下的去噪结果比较。可以看出,MF和ACWMF的去噪结果仍然包含大量噪声。维纳滤波器、GSAP 和小波方法无效。 BPDF很好地保留了细节,但它创造了雨滴效果,表现为飞机轮廓上的条纹。这在平面的边缘可以清楚地看到,如果我们将噪声级别提高得更高,雨滴效果会更强。虽然 ABF 可以很好地保留细节,但 SnP 噪声仍然存在。 SSTV 总体上很好地去除了噪音,但它产生了许多阶梯状伪影,如背景中的云层以及平面上的模糊伪影所示。对于TVL1的去噪结果,飞机的头部丢失了。飞机的其他细节没有得到很好的保存。所提出的方法有效地去除了噪声,并保留了一般结构。细节保存得很好,除了一些小细节,比如飞机尾部的字母A丢失了。总体而言,该方法的去噪效果良好,PSNR 和 SSIM 值最高。
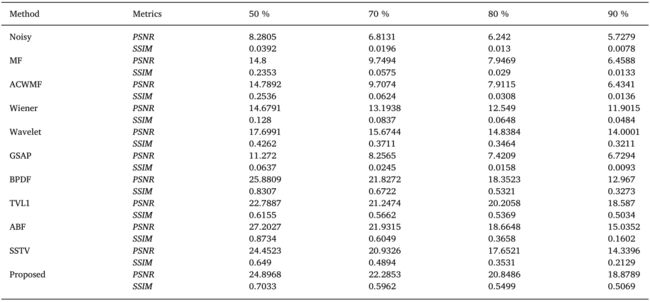
表1给出了噪声水平分别为50%、70%、80%和90%的去噪结果的平均PSNR和平均SSIM值。对于50%的噪声水平,所提出的方法只遵循BPDF和ABF的PSNR和SSIM度量。在噪声水平为70%的情况下,该方法的去噪结果的平均PSNR值高于BPDF和ABF,但平均SSIM值仍然低于BPDF和ABF。在80%和90%的噪声水平下,我们的方法的去噪结果的平均PSNR值和平均SSIM值最高。特别是,由于我们的模型是基于自适应参数估计的全变差,我们注意到表1中先前的TVL1所获得的改进。在高SNP噪声水平下,所提出的自适应电视去噪方法在PSNR和SSIM值上都优于TVL1,这在图6中真实自然图像上的视觉上得到了证实。尽管获得了良好的结果,但我们相信,通过以多尺度方式仔细选择正则化参数[5],可以获得进一步的改进,这可以帮助我们保留较小的纹理(参见图6,前置引擎)。这种纹理保留在其他图像处理以及深度学习分类和检索任务中是重要的,其中图像去噪是不可或缺的一部分。
| 表 1 不同噪声水平方法去噪结果的平均 PSNR 和平均 SSIM 值 |
|---|
 |
4.Conclusion
在文章中,我们提出了一种自适应总变分椒盐图像去噪方法。我们的方法基于一阶总变分、数据保真度的 L1 范数和自适应正则化参数估计。去噪算法是基于原始对偶梯度法实现的。从具有各种噪声水平的各种去噪结果中,我们证实了所提出的方法有效地去除了合成和真实自然图像中的噪声。对于低密度和中密度噪声,所有细节都保留得很好。对于高密度噪声,一些细节丢失了,但是与中值滤波器、维纳滤波器、小波去噪、自适应双边滤波器和正则化区域等最近的一些相关代表性方法相比,我们提出的模型中图像的主要结构仍然保留得很好.所提出的方法可以扩展到对彩色图像进行去噪。扩展到颜色和多光谱 SnP 去噪并在我们的自适应正则化参数估计中添加纹理保持组件是我们目前在这个方向上的工作。
References
[1] J. Shim, M. Yoon, Y. Lee, Feasibility of newly designed fast non local means (FNLM)-based noise reduction filter for X-ray imaging: a simulation study, Optik 160(2018) 124–130.
[1]J.Shim,M.Yoon,Y.Lee,新设计的基于快速非局部平均(FNLM)的降噪过滤器用于X射线成像的可行性:模拟研究,Optik 160。
(2018)124-130。
[2] R. Rojas, P. Rodriguez, “Spatially adaptive total variation image denoising under Salt and pepper noise,”, 19th European Signal Processing Conference EUSIPCO,Barcelona, 2011, pp. 278–282.
[2]R.Rojas,P.Rodriguez,“盐和胡椒噪声下的空间自适应全变差图像去噪”,第19届欧洲信号处理会议EUSIPCO,巴塞罗那,2011年,第278-282页。
[3] D.N.H. Thanh, S. Dvoenko, “A denoising of biomedical images,” the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences XL (5) (2015) 73–78.
[3]D.N.H.Thanh,S.Dvoenko,“生物医学图像去噪”,国际摄影测量、遥感和空间信息科学档案馆XL(5)(2015)73-78。
[4] V.B.S. Prasath, D.N.H. Thanh, N.H. Hai, “Regularization parameter selection in image restoration with inverse gradient: single scale or multiscale,”, IEEE 7th International Conference on Communications and Electronics, Hue, 2018, pp. 278–282.
[4]V.B.S.Prasath,D.N.H.Thanh,N.H.Hai,《图像恢复中的正则化参数选择:单尺度还是多尺度》,IEEE第七届国际通信与电子会议,pp,2018年,第278-282页。
[5] D.N.H. Thanh, V.B.S. Prasath, N.V. Son, L.M. Hieu, “An adaptive image inpainting method based on the modified mumford-shah model and multiscale parameter estimation”, Comput. Opt. 43 (2) (2019) 251–257.
[5]D.N.H.Thanh,V.B.S.Prasath,N.V.Son,L.M.Hieu,《基于改进的Mumford-Shah模型和多尺度参数估计的自适应图像修复方法》,Comput。选择。43(2)(2019)251-257。
[6] T.F. Chan, J. Shen, Image Processing and Analysis: Variational, PDE, Wavelet and Stochastic Methods, SIAM, 2005.
[6]陈天福,沈军,图像处理与分析:变分、偏微分方程、小波与随机方法,SIAM,2005。
[7] D.N.H. Thanh, E. Uğur, V.B.S. Prasath, V. Kumar, N.N. Hien, “A skin lesion segmentation method for dermoscopic images based on adaptive thresholding with normalization of color models,”, IEEE 2019 6th International Conference on Electrical and Electronics Engineering, Istanbul, 2019.
[7]D.N.H.Thanh,E.Uğur,V.B.S.Prasath,V.Kumar,N.N.Hien,《一种基于颜色模型归一化自适应阈值的皮肤镜图像皮肤病变分割方法》,IEEE2019第六届国际电工电子工程会议,伊斯坦布尔,2019年。
[8] V. Naghashi, “Co-occurrence of adjacent sparse local ternary patterns: a feature descriptor for texture and face image retrieval,”, Optik 157 (2018) 877–889.
[8]V.Naghashi,“相邻稀疏局部三元模式的共现:用于纹理和人脸图像检索的特征描述符”,Optik 157(2018)877-889。
[9] V.B.S. Prasath, D.N.H. Thanh, “Structure tensor adaptive total variation for image restoration,”, Turk. J. Electr. Eng. Comput. Sci. 27 (2) (2019) 1147–1156.
[9]V.B.S.Prasath,D.N.H.Thanh,《用于图像恢复的结构张量自适应全变分》,土耳其。J.伊莱特。英语。电脑。SCI。27(2)(2019)1147-1156。
[10] D.N.H. Thanh, V.B.S. Prasath, L.M. Hieu, A review on CT and X-Ray images denoising methods, Informatica 43 (2) (2019) 151–159.
[10]D.N.H.Thanh,V.B.S.Prasath,L.M.Hieu,CT和X射线图像去噪方法综述,Informatica 43(2)(2019)151-159.。
[11] K.A. Hemant, M. Angshul, Generalized synthesis and analysis Prior algorithms with application to impulse denoising, Proceedings of the 2014 Indian Conference on Computer Vision Graphics and Image Processing, Bangalore, 2014.
[11]K.A.Hemant,M.Angshul,广义综合和分析先验算法及其在脉冲去噪中的应用,2014印度计算机视觉图形和图像处理会议论文集,班加罗尔,2014。
[12] U. Erkan, L. Gokrem, A new method based on pixel density in salt and pepper noise removal, Turk. J. Electr. Eng. Comput. Sci. 26 (2018) 162–171.
[12]U·Erkan,L.Gokrem,一种基于像素密度的椒盐噪声去除新方法,土耳其。J.伊莱特。英语。电脑。SCI。26(2018)162-171。
[13] D.N.H. Thanh, S. Dvoenko, A method of total variation to remove the mixed Poisson-Gaussian noise, Pattern Recognit. Image Anal. 26 (2) (2016) 285–293.
[13]D.N.H.Thanh,S.Dvoenko,一种去除混合泊松-高斯噪声的全变分方法,模式识别。影像肛门。26(2)(2016)285-293。
[14] D.N.H. Thanh, V.B.S. Prasath, L.T. Thanh, Total variation L1 fidelity Salt-and-pepper denoising with adaptive regularization parameter, IEEE 5th Nafosted Conference on Information and Computer Science NCIS’18, Ho Chi Minh City, 2018.
[14]D.N.H.Thanh,V.B.S.Prasath,L.T.Thanh,总变分L1保真度自适应正则化参数的椒盐去噪,IEEE第五届Nafosted信息与计算机科学会议NCIS‘18,胡志明市,2018。
[15] J.S. Lim, Two-dimensional Signal and Image Processing, Prentice-Hall, New Jersey, 1990.
[15]J.S. Lim,,二维信号与图像处理,新泽西,1990。
[16] H. Hwang, R.A. Haddad, Adaptive median filters: new algorithms and results, IEEE Trans. Image Process. 4 (4) (1995) 499–502.
[16]H.Hwang,R.A.Haddad,自适应中值滤波:新算法和结果,IEEE学报。图像处理。4(4)(1995)499-502。
[17] T. Chen, H.R. Wu, Adaptive impulse detection using center-weighted median filters, IEEE Signal Process. Lett. 8 (1) (2001) 1–3.
[17]T.Chen,Wu H.R.基于中心加权中值滤波的自适应脉冲检测,IEEE信号处理。Lett。8(1)(2001)1-3。
[18] F. Jin, P. Fieguth, L. Winger, E. Jernigan, “Adaptive Wiener filtering of noisy images and image sequences,”, Proceedings 2003 International Conference on Image Processing, Barcelona, 2003.
[18]F.jin,P.Figuth,L.Winger,E.Jernigan,《噪声图像和图像序列的自适应维纳滤波》,2003年巴塞罗那国际图像处理会议论文集,2003年。
[19] X. Zhang, Image denoising using local Wiener filter and its method noise, Optik 127 (2016) 6821–6828.
[19]张晓华,基于局部维纳滤波的图像去噪及其噪声方法,Optik 127(2016)6821-6828.。
[20] C. Tomasi, R. Manduchi, Bilateral filtering for gray and color images, IEEE The International Conference on Computer Vision (ICCV’98), Bombay, 1998.
[20]C.Tomasi,R.Manduchi,灰度和彩色图像的双边过滤,IEEE国际计算机视觉会议(ICCV‘98),孟买,1998。
[21] S.V. Priya, R. Seshasayanan, Impulse noise removal using adaptive bilateral filter with robust noise detector, J. Comput. Theor. Nanosci. 13 (12) (2016)9090–9097.
[21]S.V.Priya,R.Seshasayanan,使用自适应双边滤波和稳健噪声检测器去除脉冲噪声,J.Comput。西奥。纳诺西。13(12)(2016)9090-9097。
[22] I.M. Johnstone, B.W. Silverman, Needles and Straw in haystacks: empirical bayes estimates of possibly sparse sequences, Ann. Stat. 32 (4) (2004) 1594–1649.
[22]I.M.Johnstone,B.W.Silverman,《干草堆中的针和稻草:可能稀疏序列的经验贝叶斯估计》,Ann。统计一下。32(4)(2004)1594-1649。
[23] F. Abramovich, Y. Benjamini, D.L. Donoho, I.M. Johnstone, Adapting to unknown sparsity by controlling the false discovery rate, Ann. Stat. 34 (2) (2006)584–653.
[23]F.Abramovich,Y.Benjamini,D.L.Donoho,I.M.Johnstone,通过控制错误发现率适应未知稀疏性,Ann。统计一下。34(2)(2006)584-653。
[24] A. Antoniadis, G. Oppenheim, Wavelets and statistics, Lecture Notes in Statistics, Springer Verlag, New York, 1995.
[24]A.Antoniadis,G.Oppenheim,小波与统计,统计学讲稿,Springer Verlag,纽约,1995。
[25] D.L. Donoho, De-noising by Soft-Thresholding, IEEE Trans. Inf. Theory 42 (3) (1995) 613–627.
[25]D.L.Donoho,软阈值去噪,IEEE Trans.。信息。理论42(3)(1995)613-627。
[26] A.K. Aggarwal, A. Majumdar, Hyperspectral image denoising using spatio-spectral total variation, IEEE Geosci. Remote. Sens. Lett. 13 (3) (2016) 442–446.
[26]A.K.Aggarwal,A.Majudar,使用空间光谱总变分的高光谱图像去噪,IEEE Geosi。很遥远。感官,莱特。13(3)(2016)442-446。
[27] T.F. Chan, S. Esedoglu, Aspects of total variation regularized L1 function approximation, SIAM J. Appl. Math. 65 (5) (2005) 1817–1837.
[27]T.F.Chan,S.Esedoglu,全变分正则L1函数逼近的几个方面,SIAM J.应用.。数学课。65(5)(2005)1817-1837。
[28] T.F. Chan, G.H. Golub, P. Mulet, A nonlinear primal-dual method for total variation-based image restoration, SIAM J. Sci. Comput. 20 (6) (1999) 1964–1977.
[28]陈天福,G.H.Golub,P.Mulet,一种基于全变差的非线性原始-对偶图像恢复方法,SIAM J.Sci.。电脑。20(6)(1999)1964-1977。
[29] Z. Zhi, B. Shi, Y. Sun, Primal-dual method to smoothing TV-based model for image denoising, J. Algorithm. Comput. Technol. 10 (4) (2016) 235–243.
[29]Z.Zhi,Shib,Y.Sun,原始对偶方法基于平滑TV的图像去噪模型,J.算法。电脑。泰克诺。10(4)(2016)235-243。
[30] P. Arbelaez, C. Fowlkes and D. Martin, “The Berkeley Segmentation,” UC-Berkeley, [Online]. Available: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/. [Accessed 10 12 2018].
[30]P.Arbelaez,C.Fowlkes和D.Martin,《伯克利分部》,加州大学伯克利分校,[在线]。提供:https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/.。[访问10 12 2018].
[31] V.B.S. Prasath, D. Vorotnikov, R. Pelapur, S. Jose, G. Seetharaman, K. Palaniappan, Multiscale tikhonov-total variation image restoration using spatially varying edge coherence exponent, IEEE Trans. Image Process. 24 (12) (2015) 5220–5235.
[31]V.B.S.Prasath,D.Vorotnikov,R.Pelapur,S.Jose,G.Seetharaman,K.Palaniappan,多尺度Tikhonov-使用空间变化边缘相干指数的全变差图像恢复,IEEE Transans。图像处理。24(12)(2015)5220-5235。
[32] L. Rudin, S. Osher, E. Fatemi, Nonlinear total variation based noise removal algorithms, Physica D 60 (1–4) (1990) 259–268.
[32]L.Rudin,S.Osher,E.Fatei,基于非线性全变分的噪声去除算法,Physica D 60(1-4)(1990)259-268.。
[33] H. Hu, J. Froment, Nonlocal total variation for image denoising, IEEE 2012 Symposium on Photonics and Optoelectronics, Shanghai, 2012.
[33]胡海华,J.Froment,图像去噪的非局部全变分,IEEE 2012光子学与光电子学研讨会,上海,2012。
[34] W. Lu, J. Duan, Z. Qiu, Z. Pan, R.W. Liu, L. Bai, Implementation of high‐order variational models made easy for image processing, Math. Methods Appl. Sci. 39(14) (2016) 4208–4233.
[34]陆文伟,段军中,邱振中,潘宗伟,刘荣文,白立中,高阶变分模型的实现简化了图像处理,数学。方法应用。SCI。39(14)(2016)4208-4233。
[35] D. Li, X. Tian, Q. Jin, K. Hirasawa, Adaptive fractional-order total variation image restoration with split Bregman iteration, ISA Trans. 82 (2018) 210–222.
[35]李东华,田小新,金启中,平泽,基于分裂Bregman迭代的自适应分数阶全变差图像复原,ISA Transans.。82(2018)210-222。
[36] T. Ringholm, J. Lazicyz, C.-B. Schönlieb, Variational image regularization with Euler’s elastica using a discrete gradient scheme, SIAM J. Imaging Sci. 11 (4)(2018) 2665–2691.
[36]T.Ringholm,J.Lazicyz,C.-B.Schönlieb,Euler‘s Elastica的变分图像正则化使用离散梯度方案,SIAM J.成像科学。11(4)(2018)2665-2691。
[37] V.B.S. Prasath, D.N.H. Thanh, N.H. Hai, On selecting the appropriate scale in image selective smoothing by nonlinear diffusion, IEEE 7th International Conference of Communications and Electronics, Hue, 2018, pp. 267–272.
[37]V.B.S.Prasath,D.N.H.Thanh,N.H.Hai,《在非线性扩散的图像选择性平滑中选择合适的尺度》,IEEE第七届国际通信和电子会议,色调,2018年,第267-272页。
[38] V.B.S. Prasath, D.N.H. Thanh, N.H. Hai, N.X. Cuong, Image restoration with total variation and iterative regularization parameter estimation, The Eighth International Symposium on Information and Communication Technology SoICT, NhaTrang, 2017, pp. 378–384.
[38]V.B.S.Prasath,D.N.H.Thanh,N.H.Hai,N.X.Cuong,全变分图像恢复和迭代正则化参数估计,第八届信息与通信技术国际研讨会,NhaTrang,2017,第378-384页。
[39] D.N.H. Thanh, S. Dvoenko, D.V. Sang, Colour image denoising based on a combined model, Seventh Symposium on Information and Communication Technology, Ho Chi Minh City, 2016, pp. 308–315.
[39]D.N.H.Thanh,S.Dvoenko,D.V.Sang,基于组合模型的彩色图像去噪,胡志明市第七届信息与通信技术研讨会,2016,第308-315页。
[40] Z. Wang, A. Bovik, H. Sheikh, E. Simoncelli, Image quality assessment: from error visibility to structural similarity, IEEE Trans. Image Process. 13 (4) (2004)600–612.
image denoising based on a combined model, Seventh Symposium on Information and Communication Technology, Ho Chi Minh City, 2016, pp. 308–315.
[39]D.N.H.Thanh,S.Dvoenko,D.V.Sang,基于组合模型的彩色图像去噪,胡志明市第七届信息与通信技术研讨会,2016,第308-315页。
[40] Z. Wang, A. Bovik, H. Sheikh, E. Simoncelli, Image quality assessment: from error visibility to structural similarity, IEEE Trans. Image Process. 13 (4) (2004)600–612.
[40]王振中,A.Bovik,H.Sheikh,E.Simoncelli,图像质量评估:从错误可见性到结构相似性,IEEE摘编。图像处理。13(4)(2004)600-612









