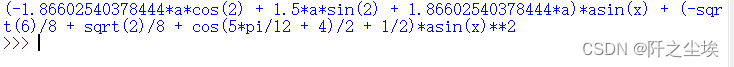Python自动化小技巧07——符号计算求方程解、二重积分
平时做高数数分的作业,手算定积分二重积分什么的太复杂了,虽然scipy能实现在方程和定积分上面求数值解,但是很多时候我们的题目里面都会带着a、x等未知参数,这个时候涉及符号运算,需要用到Python的sympy库。下面我们介绍这个库的使用,方程的求解,积分的运算。
定义符号变量
字符是题目里面的未知量,但是我们不能直接把它传入代码,因为就变成了字符串.....
我们需要先使用sympy去定义符号变量:
import sympy as sp
a,x=sp.symbols('a,x')
#或者
sp.var('a ,x ,y')
y=sp.Function('y') #符号函数上面代码展示 了两种可以把变量定义为符号变量的方法,还展示了一种定义符号函数的方法。
解方程组
我们拿最经典的一元二次方程ax^2+bx+c=0 求解试试:
import sympy as sp
a,b,c,x=sp.symbols('a,b,c,x')
x0=sp.solve(a*x**2+b*x+c,x)
print(x0)输出结果没问题
求定积分
还是拿一个简单的定积分来做案例,这样好验证对错。
我们对函数‘a*sin(x)’ 在0到π上进行积分,学过最简单的高数应该知道就是正弦函数一个拱门和x轴围城的面积,理论值应该是2a。
import sympy as sp
a,x=sp.symbols('a,x')
x0=sp.integrate(sp.sin(x)*a,(x,0,sp.pi))
print(x0)sp.integrate()里面第一个参数是要积分的函数,第二个参数是一个元组(),里面有三个参数,第一个是积分的变量,后面两个参数是这个变量的积分区间。
运行没问题。
求二重积分
这次拿一个复杂一点的函数,定义在代码里面。
import sympy as sp
sp.var('a ,x ,d')
f = sp.cos (x) *3*a/2+sp.sin(x)*(3**0.5+2)*a/2+d/2*1-sp.sin(2*x+5*sp.pi/12)*2**2*d/2
p=sp.integrate(f, (x, 0, 2), (d, 0, sp.asin(x)))
print (p)
可以看到sp.integrate()里面这次是三组参数,第一个依旧是求积分的函数,第二个是x变量和其区间,第三个是d变量和其区间。
三重积分同理,就是多一组参数。