【损失函数：2】Charbonnier Loss、SSIM Loss（附Pytorch实现）

写在前面

下面介绍各个函数时，涉及到一下2变量，其含义如下：假设网络输入为x，输出为$\overline{\text{y}}$=f(x)，x的真实标签为y，其中：
、、
上述定义中的N通常表示一个批次中所包含的样本数量，因为在网络训练时我们通常是逐批次送入网络训练，每个批次计算一次损失，然后进行参数更新。

一、Charbonnier损失

参考文章链接：http://xxx.itp.ac.cn/pdf/1710.01992

参考文章适用于图像超分辨任务，对于普通的有监督任务，Charbonnier Loss可定义为如下形式：

其中，

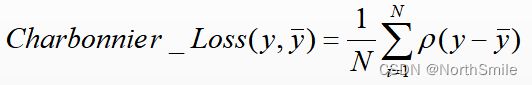
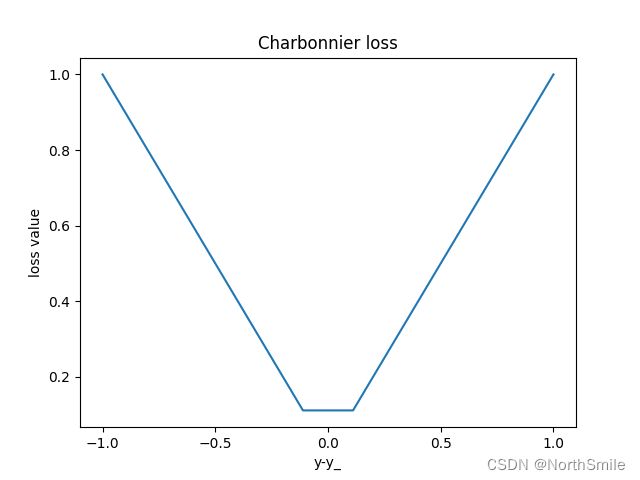
主要看一下(-1,1)这个区间内Charbonnier Loss的曲线，我们知道L1损失存在不可导点y-y_=0（见https://blog.csdn.net/qq_43665602/article/details/127037761），而Charbonnier Loss通过引入常量epslion解决了L1的缺陷，曲线在y-y_接近0的地方也可导。在此区间之外，该函数曲线近似L1损失，相比L2损失而言，对异常值不敏感，避免过分放大误差。

1）代码实现

# 4.Charbonnier Loss
class CharbonnierLoss(nn.Module):
    def __init__(self,epsilon=1e-3):
        super(CharbonnierLoss, self).__init__()
        self.epsilon2=epsilon*epsilon

    def forward(self,x):
        value=torch.sqrt(torch.pow(x,2)+self.epsilon2)
        return torch.mean(value)
creation=CharbonnierLoss()
loss=creation(y_-y)
print(loss)

tensor([[6., 6., 6., 8., 3., 6., 6., 7., 0., 5.],
        [6., 9., 7., 1., 5., 5., 6., 2., 7., 0.],
        [0., 4., 4., 6., 9., 1., 1., 4., 6., 0.],
        [8., 5., 8., 1., 7., 5., 9., 1., 4., 7.]])
tensor([[9., 4., 9., 7., 5., 5., 5., 4., 9., 6.],
        [5., 4., 8., 8., 3., 2., 7., 4., 2., 8.],
        [2., 1., 5., 3., 1., 1., 3., 9., 5., 9.],
        [8., 8., 1., 0., 1., 5., 9., 8., 9., 0.]])
-------------------------
tensor(3.2751)

二、SSIM损失

在正式介绍SSIM损失之前，我们需要先知道SSIM是什么，SSIM该如何计算？

1.结构相似性（SSIM：Structural Similartiy）

《Image Quality Assessment: From Error Visibility to Structural Similarity》中提出使用结构相似性度量进行图像质量评价任务，详细介绍了SSIM发展的由来。下面我们随原文介绍SSIM整个的定义及计算过程：
总的相似性度量定义为：

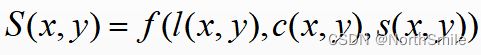
其中l(x,y)、c(x,y)和s(x,y)分别表示亮度比较、对比度比较及结构比较，三个部分相对独立，即其中任意一个成分的变化不影响其他成分，并且他们各自的定义都需要满足以下三个条件：

• 对称性：S(x,y)=S(y,x)；
• 有界性：S(x,y)<=1；
• 最大值唯一性：当且仅当x=y时（在离散表示中，x=y表示他们的对应元素均相等，即x_i=y_i），S(x,y)=1；

1）亮度比较（luminance compare）：
定义如下：

其中u_x和u_y有着类似的表示，计算输入信号的平均强度：

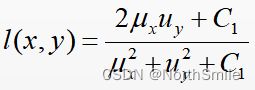
C₁是一个常量，用于避免当u_x²+u_y²接近于0时的 不稳定性，其定义如下（对于后面的C₂、C₃定义类似）：

其中K₁是一个远小于1的常数，而L表示像素值的动态范围（比如8位灰度图像L为255）.
很明显，l(x,y)的定义满足对称性等三个条件，且l(x,y)符合韦伯定律，其亮度变化ΔI与背景亮度I成正比，即ΔI/I=C，C为常数。使用R表示亮度相对背景亮度变化的大小，将失真信号表示为u_y=u_x(1+R)，由此进一步得到（假设C₁相比u_x²可忽略不不计）：

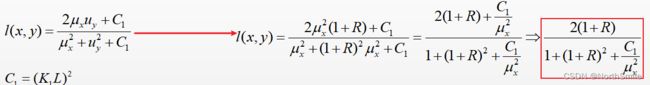
2）对比度比较（contrast compare）：
使用输入信号强度的均方差来表示对比度，均方差计算：

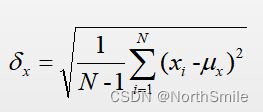
c(x,y)定义如下：

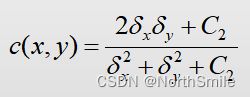
其中C₂=(K₂L)²，K₂远小于1，均为常数。
3）结构比较（structure compare）：
定义如下：

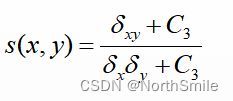
其中表示各自对应的均方差，而：

结合l(x,y)、c(x,y)和s(x,y)即可得到SSIM的计算公式：

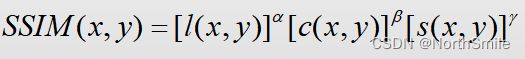
其中参数α>0，β>0，γ>0，用来调整三部分的相对重要性，简单起见均设置为1，且C₃=C₂，所以有：

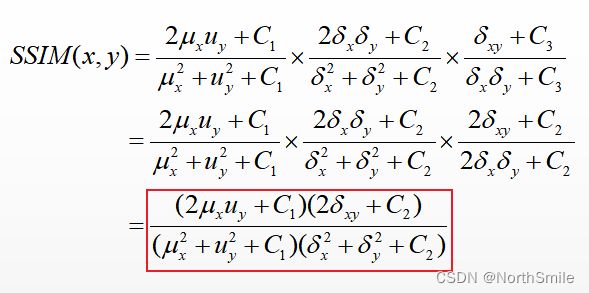
2.平均结构相似性（Mean SSIM）

前面介绍的SSIM计算公式只能计算图像中的局部区域的结构相似性，在一整幅图像中不同区域的均值、方差以及信号失真程度可能存在明显的差异，所以我们不能使用局部计算公式去衡量全局的相似性，作者提出了解决办法：MSSIM（Mean SSIM），将图像划分为多个Patch，分别计算每个Patch的局部结构相似度，再计算他们的平均值作为全局度量，此时：

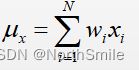
其中w_i表示每个像素点的权重，且：

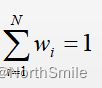
前面讲到的局部计算公式中均值计算为w_i=1/N时的特殊情况，此外：

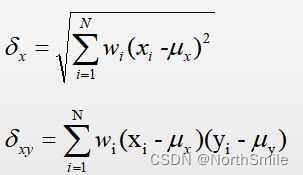
假设共有M个Patch，则全局度量为：

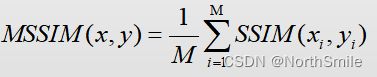
3.代码实现

在代码编写之间还需要明确几点：
1）Patch的含义
卷积操作本身就是一个“加权求和”的过程，Patch类似卷积操作中的滑动窗口，权重由卷积核的元素指定。
2）局部均值、均方差、协方差的计算
（1）局部均值通过一次卷积即可完成；
（2）均方差：方差开方；方差：

• 先将输入图像x乘方，然后对其进行卷积得到E(x²)；
• 然后对输入图像x进行卷积得到E(x)；
• 最后j计算E(x²)-E(x)²即可；

（3）类似的可得到协方差计算过程：

• 先将输入图像x、y相乘，然后对其进行卷积得到E(xy)；
• 然后分别对输入图像x、y进行卷积得到E(x)、E(y)；
• 最后计算E(xy)-E(x)E(y)即可；

下面就是最后的代码实现（在使用下面代码需要提前将输入图像像素值进行归一化处理）：

import torch
import torch.nn as nn
from torch.nn import functional as F
from torch.autograd import Variable
from PIL import Image
from torchvision import transforms
from math import exp
# 5.SSIM loss
# 生成一位高斯权重，并将其归一化
def gaussian(window_size,sigma):
    gauss = torch.Tensor([exp(-(x - window_size // 2) ** 2 / float(2 * sigma ** 2)) for x in range(window_size)])
    return gauss/torch.sum(gauss)  # 归一化


# x=gaussian(3,1.5)
# # print(x)
# x=x.unsqueeze(1)
# print(x.shape) #torch.Size([3,1])
# print(x.t().unsqueeze(0).unsqueeze(0).shape) # torch.Size([1,1,1, 3])

# 生成滑动窗口权重，创建高斯核：通过一维高斯向量进行矩阵乘法得到
def create_window(window_size,channel=1):
    _1D_window = gaussian(window_size, 1.5).unsqueeze(1)  # window_size,1
    # mm:矩阵乘法 t:转置矩阵 ->1,1,window_size,_window_size
    _2D_window = _1D_window.mm(_1D_window.t()).float().unsqueeze(0).unsqueeze(0)
    # expand:扩大张量的尺寸，比如3,1->3,4则意味将输入张量的列复制四份，
    # 1,1,window_size,_window_size->channel,1,window_size,_window_size
    window = Variable(_2D_window.expand(channel, 1, window_size, window_size).contiguous())
    return window


def _ssim(img1, img2, window, window_size, channel, size_average=True):
    mu1 = F.conv2d(img1, window, padding=window_size // 2, groups=channel)
    mu2 = F.conv2d(img2, window, padding=window_size // 2, groups=channel)

    mu1_sq = mu1.pow(2)
    mu2_sq = mu2.pow(2)
    mu1_mu2 = mu1 * mu2

    sigma1_sq = F.conv2d(img1 * img1, window, padding=window_size // 2, groups=channel) - mu1_sq
    sigma2_sq = F.conv2d(img2 * img2, window, padding=window_size // 2, groups=channel) - mu2_sq
    sigma12 = F.conv2d(img1 * img2, window, padding=window_size // 2, groups=channel) - mu1_mu2

    C1 = 0.01 ** 2
    C2 = 0.03 ** 2

    ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) * (sigma1_sq + sigma2_sq + C2))

    if size_average:
        return ssim_map.mean()
    else:
        return ssim_map.mean(1).mean(1).mean(1)


# 构造损失函数用于网络训练或者普通计算SSIM值
class SSIM(torch.nn.Module):
    def __init__(self, window_size=11, size_average=True):
        super(SSIM, self).__init__()
        self.window_size = window_size
        self.size_average = size_average
        self.channel = 1
        self.window = create_window(window_size, self.channel)

    def forward(self, img1, img2):
        (_, channel, _, _) = img1.size()

        if channel == self.channel and self.window.data.type() == img1.data.type():
            window = self.window
        else:
            window = create_window(self.window_size, channel)

            if img1.is_cuda:
                window = window.cuda(img1.get_device())
            window = window.type_as(img1)

            self.window = window
            self.channel = channel

        return _ssim(img1, img2, window, self.window_size, channel, self.size_average)


# 普通计算SSIM
def ssim(img1, img2, window_size=11, size_average=True):
    (_, channel, _, _) = img1.size()
    window = create_window(window_size, channel)

    if img1.is_cuda:
        window = window.cuda(img1.get_device())
    window = window.type_as(img1)

    return _ssim(img1, img2, window, window_size, channel, size_average)

4.测试案例

这里讲到两点：

• 仅计算图像之间的SSIM数值；
• 通过SSIM构造损失函数，进行网络训练；

输入图像：

数据读入：

# 读取数据
haze_path='./01_hazy.png'
gt_path='./01_GT.png'


def read_img(path):
    img=Image.open(path)
    return transforms.ToTensor()(img)  # 数据转为张量并进行数值归一化


haze_img,gt_img=read_img(haze_path),read_img(gt_path)
# print(type(haze_img))
haze_img,gt_img=torch.unsqueeze(haze_img,0),torch.unsqueeze(haze_img,0)

1）计算SSIM值

# 1)计算SSIM值
# 方式1
ssim_value=ssim(haze_img,gt_img)
# 方式2
ssim_loss=SSIM()(haze_img,gt_img)
print(ssim_value)
print(ssim_loss)

tensor(1.)
tensor(1.)

2）构造损失
SSIM表示输入数据之间的结构相似性，计算结果越接近于1则说明二者在结构上具有更高的相似性，所以在作为损失进行优化时，优化器需要接受的是ssim_loss的负值（优化器默认寻找的是极小值，所以需要转换为负值，如此等价于原值求极大值）。

# 2）构造损失
haze_img,gt_img=Variable(haze_img,requires_grad=True),Variable(gt_img,requires_grad=False)


ssim_loss=SSIM()
optimizer=torch.optim.Adam([haze_img],lr=0.01)

# 初始化变量
ssim_value=ssim(haze_img,gt_img)
train_steps=0
for epoch in range(10):
    print("epoch:",epoch)
    # 训练过程
    while ssim_value<0.95:
        print("train times:", train_steps)
        ssim_value=-ssim_loss(haze_img,gt_img)
        optimizer.zero_grad()
        ssim_value.backward()
        optimizer.step()
        train_steps+=1

epoch: 0
epoch: 1
epoch: 2
epoch: 3
epoch: 4
epoch: 5
epoch: 6
epoch: 7
epoch: 8
epoch: 9

输出结果很好解释，因为这里两张图象SSIM为1，内层循环不执行，主要是给大家看看SSIM Loss的一个代码框架。

参考：

1）https://blog.csdn.net/qq_35914625/article/details/113789903
2）https://github.com/Po-Hsun-Su/pytorch-ssim