Matlab线性规划函数linprog-小白详解
Matlab线性规划linprog函数
最近开始想学一学数学建模的相关知识,也找了不少视频,感觉无论是PPT做的还是讲解内容没有看起来很舒服的,只能多找几个版本多看几遍然后做一下笔记,先从最基础的线性规划函数开始写。
假设需要解决以下这个线性规划问题
m a x z = 2 x 1 + 3 x 2 − 5 x 3 s . t . { x 1 + x 2 + x 3 = 7 2 x 1 − 5 x 2 + x 3 ≥ 10 x 1 + 3 x 2 + x 3 ≤ 12 x 1 , x 2 , x 3 ≥ 0 max\quad z = 2x_1+3x_2-5x_3\\s.t. \begin{cases} x_1+x_2+x_3=7 \\ 2x_1-5x_2+x_3\geq10 \\ x_1+3x_2+x_3\leq12 \\ x_1,x_2,x_3\geq0 \end{cases} maxz=2x1+3x2−5x3s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧x1+x2+x3=72x1−5x2+x3≥10x1+3x2+x3≤12x1,x2,x3≥0
z = x 1 + 2 x 2 + 5 x 3 z = x_1+2x_2+5x_3 z=x1+2x2+5x3就是目标函数,求解的目的就是求满足条件的 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3的这三个变量的值使 z z z的值最大,用到的理论其实是我研一上的一门课程优化方法里的单纯型法,是可以手算的,但是从应用角度讲用Matalb函数就可以直接得到结果,似乎参加数学建模不需要十分掌握原理。
那知道了规划问题那怎么将这些线性规划问题的系数输入到函数中呢
linprog函数的对应公式
x = l i n p r o g ( f , A , b ) x = linprog(f,A,b) x=linprog(f,A,b)
x = l i n p r o g ( f , A , b , A e q , b e q ) x = linprog(f,A,b,Aeq,beq) x=linprog(f,A,b,Aeq,beq)
x = l i n p r o g ( f , A , b , A e q , b e q , l b , u b ) x = linprog(f,A,b,Aeq,beq,lb,ub) x=linprog(f,A,b,Aeq,beq,lb,ub)
linprog参数的对应公式如下
m i n f x s . t . { A x ≤ b A e q ⋅ x = b e q l b ≤ x ≤ u b min\quad fx\\ s.t. \begin{cases} Ax\leq b \\ Aeq\cdot x=beq\\ lb\leq x \leq ub \end{cases} minfxs.t.⎩⎪⎨⎪⎧Ax≤bAeq⋅x=beqlb≤x≤ub
在变量数量大于1时 f , A , A e q , l b , u b f,A,Aeq,lb,ub f,A,Aeq,lb,ub这些参数都是矩阵 b , b e q b,beq b,beq这两个参数根据不等式和等式的数量可能是一个数也可能是一个矩阵。
在实际应用时就是将原规划转换成公式所需的的形式,然后将对应的系数参数提取出来,输入到函数中进行求解。
这里值得注意到的是 l i n p r o g linprog linprog函数只能求最小值,以及约束的条件只能是小于等于,所以需要对原来的线性规划进行一些转化,让线性规划的的目标变成求最小值,并且让约束条件都变成小于等于
让约束变成小于等于很简单左右两边都乘一个负号就行了那把 2 x 1 − 5 x 2 + x 3 ≥ 10 2x_1-5x_2+x_3\geq10 2x1−5x2+x3≥10这个约束条件左右加一个负号变成 − 2 x 1 + 5 x 2 − x 3 ≤ 10 -2x_1+5x_2-x_3\leq10 −2x1+5x2−x3≤10放到一起
m a x z = 2 x 1 + 3 x 2 − 5 x 3 s . t . { x 1 + x 2 + x 3 = 7 − 2 x 1 + 5 x 2 − x 3 ≤ 10 x 1 + 3 x 2 + x 3 ≤ 12 x 1 , x 2 , x 3 ≥ 0 max\quad z = 2x_1+3x_2-5x_3\\s.t. \begin{cases} x_1+x_2+x_3=7 \\ -2x_1+5x_2-x_3\leq10 \\ x_1+3x_2+x_3\leq12 \\ x_1,x_2,x_3\geq0 \end{cases} maxz=2x1+3x2−5x3s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧x1+x2+x3=7−2x1+5x2−x3≤10x1+3x2+x3≤12x1,x2,x3≥0
接下来就是将求最大值转变为求最小值举个最简单的但是应该很有助于理解的例子
假设一个我们求函数 y = − x 2 + 5 y=-x^2+5 y=−x2+5的最大值 y = − x 2 + 5 y=-x^2+5 y=−x2+5函数图像如下,很明显最大值是 x = 0 x=0 x=0这一点此时最大值 y = 5 y=5 y=5

那求最小值是把函数图像调过来求最小值吗?可以看到此时的函数 y 1 = x 2 − 5 y_1=x^2-5 y1=x2−5最小值是是 x = 0 x=0 x=0这一点此时最大值 y 1 = − 5 y_1=-5 y1=−5
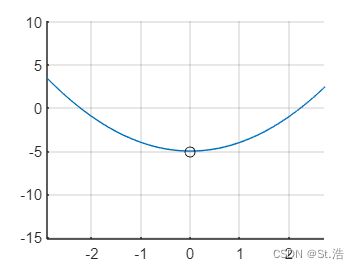
但是我们求解的 y = − x 2 + 5 y=-x^2+5 y=−x2+5函数的最大值是5实际上是 y = x 2 − 5 y=x^2-5 y=x2−5函数最小值的负数。那应该怎么理解呢
假设对于 y = − x 2 + 5 y=-x^2+5 y=−x2+5最大值解为 x = x ∗ x=x^* x=x∗, y = y ∗ y=y^* y=y∗则 y ∗ = − x ∗ 2 + 5 y^*=-x^{*2}+5 y∗=−x∗2+5 对两边取负值则 − y ∗ = x ∗ 2 − 5 -y^*=x^{*2}-5 −y∗=x∗2−5 之前我们将 − y ∗ -y^* −y∗看成 y 1 y_1 y1所以求得的 y 1 = x 2 − 5 y_1=x^2-5 y1=x2−5中的最小值 y 1 ∗ y_1^* y1∗其实是 − y ∗ -y^* −y∗也就是 y = − x 2 + 5 y=-x^2+5 y=−x2+5最大值解的负数
因此我们将原线性规划问题变为
m i n z 1 = − 2 x 1 − 3 x 2 + 5 x 3 s . t . { x 1 + x 2 + x 3 = 7 − 2 x 1 + 5 x 2 − x 3 ≤ 10 x 1 + 3 x 2 + x 3 ≤ 12 x 1 , x 2 , x 3 ≥ 0 min\quad z_1 = -2x_1-3x_2+5x_3\\s.t. \begin{cases} x_1+x_2+x_3=7 \\ -2x_1+5x_2-x_3\leq10 \\ x_1+3x_2+x_3\leq12 \\ x_1,x_2,x_3\geq0 \end{cases} minz1=−2x1−3x2+5x3s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧x1+x2+x3=7−2x1+5x2−x3≤10x1+3x2+x3≤12x1,x2,x3≥0
其中 z 1 = − z z_1=-z z1=−z
好了我们已经将原问题转换为了符合使用linprog函数的形式接下来就是将函数所需要的每一个参数找出来然后放进函数里去求解,再把这个公式站过来,首先找 f f f
m i n f x s . t . { A x ≤ b A e q ⋅ x = b e q l b ≤ x ≤ u b min\quad fx\\ s.t. \begin{cases} Ax\leq b \\ Aeq\cdot x=beq\\ lb\leq x \leq ub \end{cases} minfxs.t.⎩⎪⎨⎪⎧Ax≤bAeq⋅x=beqlb≤x≤ub
f x = [ − 2 − 3 5 ] [ x 1 x 2 x 3 ] fx=\left[\begin{array}{c}-2 & -3 & 5 \end{array}\right]\left[\begin{array}{c}x_1 \\ x_2 \\ x_3 \end{array}\right] fx=[−2−35]⎣⎡x1x2x3⎦⎤
所以
f = [ − 1 − 2 − 5 ] f=\left[\begin{array}{c}-1 & -2 & -5 \end{array}\right] f=[−1−2−5]
然后再来找 A A A
A x = [ − 2 5 − 1 1 3 1 ] [ x 1 x 2 x 3 ] Ax=\left[\begin{array}{c}-2 & 5 & -1 \\1 & 3 & 1 \end{array}\right]\left[\begin{array}{c}x_1 \\ x_2 \\ x_3 \end{array}\right] Ax=[−2153−11]⎣⎡x1x2x3⎦⎤
所以A为
A = [ − 2 5 − 1 1 3 1 ] A=\left[\begin{array}{c}-2 & 5 & -1 \\1 & 3 & 1 \end{array}\right] A=[−2153−11]
则 b b b为
b = [ − 10 12 ] b=\left[\begin{array}{c}-10 \\ 12 \end{array}\right] b=[−1012]
然后是
A e q ⋅ x = [ 1 1 1 ] [ x 1 x 2 x 3 ] Aeq\cdot x=\left[\begin{array}{c}1 & 1 & 1 \end{array}\right]\left[\begin{array}{c}x_1 \\ x_2 \\ x_3 \end{array}\right] Aeq⋅x=[111]⎣⎡x1x2x3⎦⎤
A e q = [ 1 1 1 ] Aeq=\left[\begin{array}{c}1 & 1 & 1 \end{array}\right] Aeq=[111]
这里由于等式约束只有一个所以 b e q = 7 beq=7 beq=7是一个数
因为原规划中 x 1 , x 2 , x 3 ≥ 0 x_1,x_2,x_3\geq0 x1,x2,x3≥0只有下限没有上限 l b ≤ x ≤ u b lb\leq x \leq ub lb≤x≤ub所以只需要输入 l b lb lb,这里的 l b lb lb就是
l b = [ 0 0 0 ] lb=\left[\begin{array}{c}0 \\ 0 \\0 \end{array}\right] lb=⎣⎡000⎦⎤
[ x 1 x 2 x 3 ] ≥ [ 0 0 0 ] \left[\begin{array}{c}x_1 \\ x_2 \\ x_3 \end{array}\right]\geq\left[\begin{array}{c}0 \\ 0 \\0 \end{array}\right] ⎣⎡x1x2x3⎦⎤≥⎣⎡000⎦⎤
当分解出了所有的参数了之后用matlab进行编程
f = [-2 -3 5];
A = [-2 5 -1; 1 3 1];
b = [-10; 12];
Aeq=[1 1 1];
Beq=7;
lb = zeros(3,1);
[x,z1] = linprog(f,A,b,Aeq,Beq,lb);
z=-z1
最后的结果如下,最优解为
x ∗ = [ 6.4286 0.5714 0 ] x^*=\left[\begin{array}{c}6.4286 \\ 0.5714 \\0 \end{array}\right] x∗=⎣⎡6.42860.57140⎦⎤
最优值 z ∗ = 14.5714 z^*=14.5714 z∗=14.5714
