机器学习——概率模型

概述——用一类图来表达变量相关关系的概率模型（概率模型将学习任务归结于计算变量的概率分布）

P(A|B)=P(A,B)/P(B)——根据联合概率 P(A,B)推断  P(A|B)的过程

具体说：假定所关心的变量集合为 Y，可观测变量集合为 O，其他变量的集合为 R

“生成式”模型：考虑联合分布 P(Y,R,O)

”判别式“模型：考虑联合分布 P(Y,R|O)

“推断”——利用已知变量推测未知变量的分布——核心是：如何基于可观察变量推测出未知变量的条件分布；

          ——给定一组观测变量值，由 P(Y,R,O) 或 P(Y,R|O) 得到条件概率  P(Y|O)

已知图模型	有向图模型——贝叶斯网
	无向图模型——马尔科夫随机场
未知图模型	“评分搜索”——根据训练数据集找出结构最恰当的贝叶斯网

 

 

 

 

1.贝叶斯网/信念网——借助有向无环图图来刻画属性之间的依赖关系，并使用条件概率表来描述属性的联合概率分布 

1.1贝叶斯网三种典型依赖关系

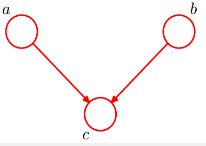
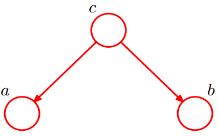
V型结构也成冲撞结构	同父结构	顺序结构

 V型结构也成冲撞结构：给定c的取值，a,b必不独立，但是当c的取值不知道时，a,b反而独立

同父结构：当c已知时，a和b独立

顺序结构：如果已知C，那么a和b条件独立

1.2“有向分离”——分析有向图中变量间的条件独立性

步骤  1）把有向图转变一个无向图

              找出有向图中所有V型结构，在V型结构的两个父结点之间加上一条无向边；

              将所有有向边改为无向边，由此产生的无向图称为“道德图”

          2）基于道德图找到变量间的条件独立性

              假定道德图中有变量x,y和变量集合z={Zi},若变量x和y能在图上被z分开，即从道德图中将变量集合z去除掉后，x和y分属于两个联通分支，则称变量x和y被z有向分离；

1.3结构

以结构表达了属性之间的条件独立性，给定父节点集，假设每个属性与它的非后裔属性独立，于是有联合概率分布定义为

1.4典型图结构

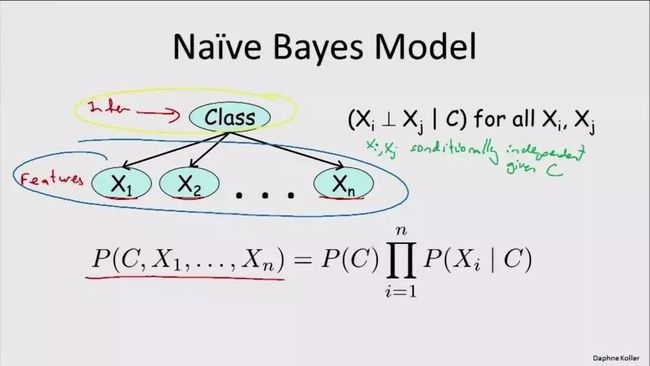
1.4.1 朴素贝叶斯分类器

联合概率的求解：

 朴素贝叶斯分类器的表达式：

1.4.2 隐马尔可夫模型 

联合概率的求解：

确定一个隐马尔可夫模型，还需要三组参数

1）状态转移概率：模型在各个状态间转换的概率,通常用矩阵表示

                                  

2）输出观测概率:根据当前状态获得各个观测值的概率，通常用矩阵表示

                                   

3）初始状态概率：模型在初始时各个状态出现的概率，通常记为：

                                  表示模型初始状态为  的概率

通过制定状态空间Y，观测空间X和以上三个参数，就确定一个隐马尔可夫模型

2.马尔可夫随机场——典型的马尔可夫网，这是一种著名的无向图模型（由无向图表示的联合概率分布）

随机变量间三种典型关系：

  1）全局马尔可夫性——给定随机变量组Yc条件下，随机变量组Ya,Yb是条件独立

  2）局部马尔可夫性——在给定与一个节点连接的邻接变量 w 的情况下，该节点 v 与其他变量 o 条件独立

  3）成对马尔可夫性——描述两个节点条件独立

概率无向图模型的因子分解——将概率无向图模型的联合概率分布表示为其最大团上随机变量的函数的乘积形式

 势函数——定量刻画变量间的相互关系；为了满足非负性，指数函数常被用于定义势函数

条件随机场——主要讨论定义在线性链上的条件随机场