Pytorch：优化器、损失函数与深度神经网络框架

Pytorch: 优化器、损失函数与深度神经网络框架

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

这章内容非常重要，需要大家有一定的机器学习基础，尤其是梯度下降法和损失函数，没有这方面基础，又不太看得懂教程的可以去看如下几个知识点：梯度下降法，随机梯度下降法，均方误差，交叉熵，Logistic Regression，模型的过拟合与欠拟合。

Reference

优化器算法索引网站

Adam 优化器相关论文

各类优化器的论文

优化器

梯度下降是所有机器学习算法的基础，没有这方面经验的同学可以自己查阅相关资料，深入理解背后的数学知识和优化思想。

https://ruder.io/optimizing-gradient-descent/ 是个非常好用的优化器算法索引链接，大家可以用这个链接去找不同的优化器原理。

梯度下降(GD)

在深度学习网络中，通常需要设计一个模型的损失函数来约束我们的训练过程，如针对分类问题可以使用交叉嫡损失，针对回归问题可以使用均方根误差损失等。模型的训练并不是漫无目的的，而是朝着最小化损失函数的方向去训练，这时就会用到梯度下降类的算法。

梯度下降法(gradient descent)是一个阶最优化算法， 是通过函数当前点对应梯度(或者是近似梯度)的反方向，使用规定步长距离进行迭代搜索，从而找到一一个函数的局部极小值的算法，最好的情况是希望找到全局极小值。

优化问题：考虑无约束问题 $minimizef(x)$ 。给定初始点 $x^{(0)}$ ，寻找序列 $x^{(1)},x^{(2)}\cdots$ 使函数沿着该序列单调递减。
$$f(x^{(0)})⩾f(x^{(1)})⩾f(x^{(2)})⩾\cdots$$
梯度下降即构造这样的序列，使函数最终达到一个较为满意的最小值点

梯度下降法是典型的迭代法之一，这类方法的核心，即为如何定义从上一个点到下一个点的规则，一般利用一阶导数(梯度)或者二阶导数(黑塞矩阵)。

原理：假设当前点为 $x^{(k)}$ ，则下一个点为 $x^{(k+1)}=x^{(k)}+t\Delta x^{(k)},\Delta x^{(k)}=-\nabla f(x^{(k)})$ 。

定义：下降方向。如果 $\exists t$ 使得 $f(x_0+tv)<f(x_0)$ ，则 $v$ 为 $f$ 在 $x_0$ 的下降方向。

泰勒展开：$f(x_k+\Delta x)-f(x_k)=(\Delta f(x){)}^T\Delta x+o(||\Delta x||)$

保证移动到下一个点时，函数值减小，则有：
$$\begin{array}{rl}& \Delta x>0,\nabla f(x_k)⩽0\\ & \iff \Delta x^T\nabla f(x_k)⩽0(Taylor)\\ & \iff -\nabla {f(x_k)}^T\nabla f(x_k)(令\Delta x=\nabla f(X_k))\\ & =-||\nabla f(x_k)|{|}_2^2⩽0\end{array}$$
定理：对于连续可导函数 $f$ ，如果 $v^T\nabla f(x_0)<0$ ，则 $v$ 为下降方向。
$$\begin{array}{rl}f(x^{(k+1)})& =f(x^{(k)}+t\Delta x)\\ & =f(x^{(k)}+t\nabla f(x^{(k)}{)}^T\Delta x)\\ & =f(x^{(k)}-t||\nabla f(x^{(k)})||)\end{array}$$
夹角：$\Delta x^T\nabla f(x_k)=||\Delta x||\cdot ||f(x_k)||\cdot \cos \theta$ 。则 $\theta =\pi$ ，即负梯度方向时，函数值下降得是最快的。

步长 $t$ (学习率)是用来保证 $x+\Delta x$ 在 $x$ 的邻域内，从而可以忽略泰勒公式中的 $o(||\Delta x||)$ 项。

迭代终止条件：函数的梯度值为 $0$ 或接近 $0$ ，此时认为已经达到了极值点。

算法过程：( $eps$ 为人工指定的接近 $0$ 的正数，$N$ 为最大迭代次数)
i n i t   x 0 , k = 0 w h i l e   ∣ ∣ ∇ f ( x k ) > e p s ∣ ∣   a n d   K < N : . . . x k + 1 = x k − t ∇ f ( x + k ) . . . k = k + 1 e n d   w h i l e \begin{aligned} &init\ x_0,k=0\\ &while\ ||\nabla f(x_k)>eps||\ and\ K​init x0​,k=0while ∣∣∇f(xk​)>eps∣∣ and K<N:...xk+1​=xk​−t∇f(x+k)...k=k+1end while​

最速下降

它的思想和梯度下降法类似，但是每次需要计算最佳步长 $t^{\ast }$ 。

步长确定：$t^{(k)}=\arg {\min }_{t⩾0}f(x^{(k)}-t\nabla f(x^{(k)}))$ 。

两种优化方法，第一种是取多个典型值，然后分别计算他们的目标函数值，确定最优值。第二种方法是以 $t$ 为自变量，直接求上式的逐点，对于有些情况可以得到解析解。这类方法也成为直线搜索，它沿着某一确定的方向在直线上寻找最优步长。

随机梯度下降(SGD)

在使用梯度下降算法时，每次更新参数都需要使用所有的样本。如果对所有的样本均计算一次最后取梯度平均值，当样本总量特别大时，对算法的速度和效率影响非常大。所以就有了随机梯度下降(stochastic gradient descent, SGD)算法，它是对梯度下降法算法的一种改进，即每次只使用部分样本来计算梯度。

在机器学习和深度学习中，SGD 通常指小批随机梯度下降(mini-batch gradient descent)算法，即每次只随机取一部分样本( $M\ll N$ )进行优化， 样本的数量一般是 $2$ 的整数次幂，取值范围一般是 $32\sim 256$ ，以保证计算精度的同时提升计算速度，是优化深度学习网络中最常用的一类算法。

本质上，即损失从整体样本的平均损失，变成了这个 batch 样本的损失：
$$\begin{gathered} L(w)=\frac{1}{N}\sum _{i=1}^{N}L(w,x_i,y_i)\to \\ L(w)=\frac{1}{M}\sum _{i=1}^{M}L(w,x_i,y_i) \end{gathered}$$
SGD 算法及其一些变种，是深度学习中应用最多的一类算法。其在训练过程中，通常会使用一个固定的学习率进行训练。即：

$$\begin{gathered} g_t={\nabla }_{{\theta }_{t-1}}f({\theta }_{t-1}) \\ {\theta }_t=-\eta \cdot g_t \end{gathered}$$

式中，$g_t$ 是第 $t$ 步的这 $M$ 个样本的平均梯度，$\eta$ 则是学习率，随机梯度下降算法在优化时，完全依赖于当前 batch 数据计算得到的梯度，而学习率则是调整梯度影响大小的参数，通过控制学习率 $\eta$ 的大小，一定程度上可以控制网络的训练速度。

SGD 随机采样产生的梯度的期望值是真实的梯度。在具体实现时，DataLoader 每次都要对样本进行 shuffle ，然后均匀分成多个 batch，每份 $M$ 个样本，接下来用每一份分别计算各自 batch 的梯度，最后迭代优化 $x_k$ 。由于每次优化时，并没有使用全部样本来更新，SGD 其实并不能保证每次迭代后目标函数值一定下降，但是能保证整体是呈下降趋势的，能够收敛到局部极值点处。

SGD 虽然在大多数情况下都很有效，但其还存在一些缺点。如很难确定一个合适的学习率 $\eta$ ，而且所有的参数使用同样的学习率可能并不是最有效的方法。针对这种情况，可以采用变化学习率 $\eta$ 的训练方式，如控制网络在初期以大的学习率进行参数更新，后期以小的学习率进行参数更新。随机梯度下降的另一个缺点就是，其更容易收敛到局部最优解，而且当落人局部最优解后，很难跳出局部最优解的区域。

总结，SGD 的缺点在于，很难确定一个合适的学习率，且容易收敛到局部梯度最小。

动量的变化

针对随机梯度下降算法的缺点，动量的思想被引入优化算法中。动量通过模拟物体运动时的惯性来更新网络中的参数，即更新时在一定程度上会考虑之前参数更新的方向，同时利用当前 batch 计算得到的梯度，将两者结合起来计算出最终参数需要更新的大小和方向。在优化时引人动量思想旨在加速学习，特别是面对小而连续且含有很多噪声的梯度。利用动量在一定程度上不仅增加了学习参数的稳定性，而且会更快地学习到收敛的参数。

在引入动量后，网络的参数则按照下面的方式更新:
$$\begin{gathered} g_t={\nabla }_{{\theta }_{t-1}}f({\theta }_{t-1}) \\ {m}_t=\mu \cdot m_{t-1}+g_t \\ \nabla {\theta }_t=-\eta \cdot m_t=-\eta {\nabla }_{{\theta }_{t-1}}f({\theta }_{t-1})+\mu m_{t-1} \end{gathered}$$
在上述公式中，$m_t$ 为当前动量的累加，$\mu$ 属于动量因子，用于调整上一步动量对参数更新时的重要程度。引入动量后，在网络更新初期可利用上一次参数更新，此时下降方向一致， 乘以较大的 $\mu$ 能够进行很好的加速。在网络更新后期，随着梯度 $g_t$ 逐渐趋近于 $0$ ，在局部最小值来回震荡的时候，利用动量使得更新幅度增大，跳出局部最优解的陷阱。

Nesterov 项(Nesterov 动量)是在梯度更新时做出的校正，避免参数更新太快，同时提高灵敏度。在动量中，之前累积的动量 $m_t$ 并不会直接影响当前的梯度 $g_t$ ，所以 Nesterov 的改进就是让之前的动量直接影响当前的动量，即
$$\begin{gathered} g_t={\nabla }_{{\theta }_{t-1}}f({\theta }_{t-1}-\eta \cdot \mu \cdot m_{t-1}) \\ {m}_t=\mu \cdot m_{t-1}+g_t \\ \nabla {\theta }_t=-\eta \cdot m_t \end{gathered}$$
Nesterov 动量和标准动量的区别在于，在当前 batch 梯度的计算上，Nesterov 动量的梯度计算是在施加当前速度之后的梯度。所以，Nesterov 动量可以看作是在标准动量方法上添加了一个校正因子，从而提升算法的更新性能。

自适应学习率

在训练开始的时候，参数会与最终的最优值点距离较远，所以需要使用较大的学习率，经过几轮训练之后，则需要减小训练学习率。因此，在众多的优化算法中，不仅有通过改变更新时梯度方向和大小的算法，还有一些算法则是优化了学习率等参数的变化，如一 系列 自适应学习率的算法 Adadelta、RMSProp及 Adam 等自适应学习率算法。

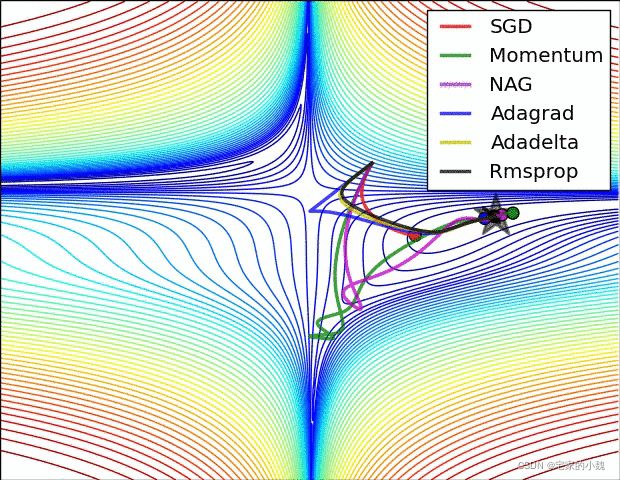
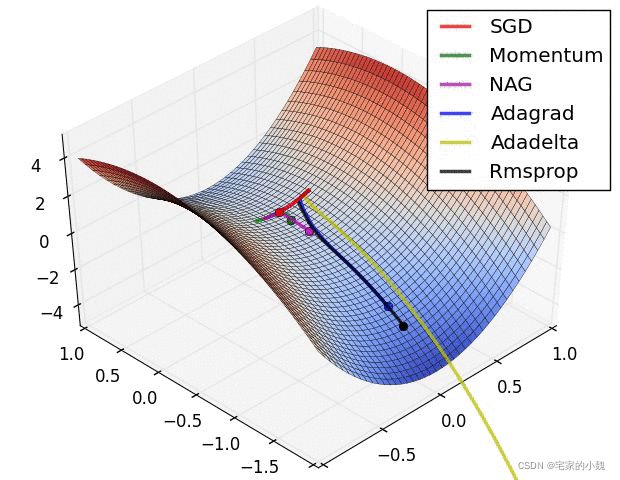
很多网站介绍了多种优化算法，如该网站在一个通用的问题下求解其路径，其过程截图如图所示(打开前记得科学上网)。

在 torch.optim 模块，提供多种深度学习的优化算法。

import torch
from torch import nn
from torch import optim
import matplotlib.pyplot as plt

torch.optim.Adadelta()
torch.optim.Adagrad()
torch.optim.Adam()
torch.optim.ASGD()    # 平均随机梯度下降
torch.optim.LBFCS()
torch.optim.RMSprop()
torch.optim.Rprop()    # 弹性反向传播  
torch.optim.SGD()     # 随机梯度下降

我们将在下面详细讲解其中常用的算法：AdaGrad, RMSProp, AdaDelta, Adam 算法。

Adaptive Gradient 算法(AdaGrad)

torch.optim.Adagrad()

AdaGrad 算法根据前几轮迭代的历史梯度值动态计算步长(学习率)值，且优化向量每一个都有自己的步长：
$$(x_{k+1}{)}_i=(x_k{)}_i-\eta \frac{(g_k{)}_i}{\sqrt{{\sum }_{j=1}^k((g_j{)}_i{)}^2+ϵ}}$$
$\eta$ 是人工设定的全局学习率，$g_k$ 是第 $k$ 次迭代时的梯度向量，$ϵ$ 是为了避免除以 $0$ 操作而增加的接近于 $0$ 的整数，$i$ 为向量的分量下标，这里的计算针对向量的每个分量分别进行。

与 GD 和 SGD 不同，它多了一个分母项，这个分母项用来累积到本次为止的梯度的历史值信息，用于计算新的步长值。历史导数值的绝对值也大，在改分量上的学习率越久越小。

这种方法存在的问题就是，他需要人工设置全局学习率 $\eta$ ；且随着时间的累积，分母项会越来越大，导致学习率为 $0$ ，模型无法更新参数

RMSProp 算法

torch.optim.RMSprop()

RMSProp 算法是对 AdaGrad 算法的改进，避免了长期累积梯度值所导致的学习率趋于 $0$ 的问题。算法维持一个梯度平方累加值的向量 $E[g^2]$ ，其初始值为 $0$ ，更新公式为：
$$E[g^2{]}_k=\delta E[g^2{]}_{k-1}+(1-\delta )g_k^2$$
这里 $g^2$ 是对梯度向量的每个分量分别进行平方，$\delta$ 是人工设定的衰减系数。和 AdaGrad 直接累加所有历史梯度的平方和不一样，RMSProp 算法将历史梯度的平方按照系数 $\delta$ 指数级衰减之后，再累加。本质上使用了移动指数加权平均，其更新公式为：
$$(x_{k+1}{)}_i=(x_k{)}_i-\eta \frac{(g_k{)}_i}{\sqrt{(E[g^2{]}_k{)}_i+ϵ}}$$
$\eta$ 是人工设定的全局学习率。

AdaDelta 算法

torch.optim.Adadelta()

AdaDelta 算法也是对 AdaGrad 算法的改进，避免了长期累积梯度值所导致的学习率趋于 $0$ 的问题，不仅如此，它还去掉了对 $\eta$ 这个全局学习率的依赖。

算法定义了两个 向量，初始值均为 $0$ (为了不依赖学习率)：
$$E[g^2{]}_0=0E[\Delta x^2{]}_0=0$$
$E[g^2]$ 和 RMSProp 算法一致，为梯度平方值，更新公式为：
$$E[g^2{]}_k=\rho E[g^2{]}_{k-1}+(1-\rho )g_k^2$$
接下来计算 RMS 向量：
$$RMS[g{]}_k=\sqrt{E[g^2{]}_k+ϵ}$$
然后计算更新值：
$$\begin{gathered} \Delta x_k=-\frac{RMS[\Delta x{]}_{k-1}}{RMS[g{]}_k}{g}_k \\ =-\frac{\sqrt{E[\Delta x^2{]}_k+ϵ}}{\sqrt{E[g^2{]}_k+ϵ}}{g}_k \end{gathered}$$
$E[\Delta x^2]$ 是优化变量更新值的平方累加值，更新公式为
$$E[\Delta x^2{]}_k=\rho E[\Delta x^2{]}_{k-1}+(1-\rho )[\Delta x_k^2$$
整体公式为：
$$(x_{k+1}{)}_i=(x_k{)}_i-\eta \frac{\sqrt{(E[\Delta x^2{]}_k{)}_i+ϵ}}{\sqrt{(E[g^2{]}_k{)}_i+ϵ}}(g_k{)}_i$$
可以看出，和 AdaGrad 算法比，AdaDelta 算法处理考虑历史梯度的平方和。和 RMSProp 算法比，除了沿用它的历史梯度的衰减机制，来避免分母项过大(导致学习率为 $0$ )；还考虑了历史变量的平方累加值，以便于去掉对人工学习率 $\eta$ 设置的依赖。

Adaptive Moment Estimation(Adam) 算法

torch.optim.Adam()

Adam 优化器结合了前面优化器的思想，综合考虑了动量项和自适应学习率。Adam 算法在 RMSProp 算法基础上对小批量随机梯度也做了指数加权移动平均。Adam 算法可以看做是 RMSProp 算法与动量法的结合。

其主要原理是，对梯度的一阶矩估计( First Moment Estimation ，即梯度的均值)和二阶矩估计( Second Moment Estimation ，即梯度的未中心化的方差)进行综合考虑，计算出每一次迭代更新步长。

Adam 算法使用了动量变量 ${\mathbf{v}}_k$ 和 RMSProp 算法中小批量随机梯度按元素平方的指数加权移动平均变量 ${\mathbf{m}}_k$，并在时间步 $0$ 将它们中每个元素初始化为 $0$ 。

给定超参数 $0\le {\beta }_1<1$ （算法作者建议设为 $0.9$ ），时间步 $k$ 的动量变量 ${\mathbf{m}}_k$ 即小批量随机梯度 ${\mathbf{g}}_k$ 的指数加权移动平均：
$$({\mathbf{m}}_k{)}_i\leftarrow {\beta }_1({\mathbf{m}}_{k-1}{)}_i+(1-{\beta }_1)({\mathbf{g}}_k{)}_i$$
和 RMSProp 算法中一样，给定超参数 $0⩽{\beta }_2<1$ （算法作者建议设为 $0.999$ ）， 将小批量随机梯度按元素平方后的项 $({\mathbf{g}}_k{)}_i^2$ 做指数加权移动平均得到学习率 ${\mathbf{v}}_k$ ，学习率衰减机制，可以确保分母项不会过大导致最后学习率为 $0$：
$$({\mathbf{v}}_k{)}_i\leftarrow {\beta }_2({\mathbf{v}}_{k-1}{)}_i+(1-{\beta }_2)({\mathbf{g}}_k{)}_i\odot ({\mathbf{g}}_k{)}_i$$
类似于 AdaDelta 算法，将 ${\mathbf{v}}_0$ 和 ${\mathbf{m}}_0$ 中的元素都初始化为 $0$ 。在时间步 $k$ 我们得到 ${\mathbf{m}}_k=(1-{\beta }_1){\sum }_{i=1}^k{\beta }_1^{k-i}{\mathbf{g}}_i$ 。引入动量思想，即将过去各时间步小批量随机梯度的权值相加，得到 $(1-{\beta }_1){\sum }_{i=1}^k{\beta }_1^{k-i}=1-{\beta }_1^k$ 。

需要注意的是，当 $k$ 较小时，过去各时间步小批量随机梯度权值之和会较小。例如，当 ${\beta }_1=0.9$ 时，${\mathbf{m}}_1=0.1{\mathbf{g}}_1$ 。为了消除这样的影响，对于任意时间步 $k$ ，我们可以将 ${\mathbf{m}}_k$ 再除以 $1-{\beta }_1^k$ ，从而使过去各时间步小批量随机梯度权值之和为 $1$ 。这也叫作偏差修正。在 Adam 算法中，我们对变量 ${\mathbf{m}}_k$ 和 ${\mathbf{v}}_k$ 均作偏差修正：
$$\begin{gathered} ({\hat{\mathbf{m}}}_k{)}_i\leftarrow \frac{({\mathbf{m}}_k{)}_i}{1-{\beta }_1^k} \\ {\widehat{(\mathbf{v}}}_k{)}_i\leftarrow \frac{({\mathbf{v}}_k{)}_i}{1-{\beta }_2^k} \end{gathered}$$

接下来， Adam 算法使用以上偏差修正后的变量 ${\hat{\mathbf{m}}}_k\leftarrow \frac{{\mathbf{m}}_k}{1-{\beta }_1^k}$ 和 ${\hat{\mathbf{v}}}_k$ ，按照 AdaGrad 算法的思路，将模型参数中每个元素的学习率通过按元素运算重新调整：
$$({\mathbf{g}}_k^{\prime }{)}_i\leftarrow \frac{\eta {\widehat{(\mathbf{m}}}_k{)}_i}{\sqrt{{\widehat{(\mathbf{v}}}_k{)}_i}+ϵ}$$
和上面介绍的几种优化算法一致， $\eta$ 是全局学习率， $ϵ$ 是为了维持数值稳定性而添加的常数，如 $10^{-8}$ 。这样，和 AdaGrad 算法、RMSProp 算法以及 AdaDelta 算法一样，目标函数自变量中每个元素都分别拥有自己的学习率。同时，Adam 也引入了动量项，保证了收敛速度。

最后，使用 ${\mathbf{g}}_k^{\prime }$ 迭代自变量：

$$\begin{array}{rl}{\mathbf{x}}_k& \leftarrow {\mathbf{x}}_{k-1}-{\mathbf{g}}_k^{\prime }\\ {\mathbf{x}}_k& \leftarrow {\mathbf{x}}_{k-1}-\eta \frac{{\mathbf{m}}_k}{\sqrt{{\hat{\mathbf{v}}}_k}+ϵ}\\ & ={\mathbf{x}}_{k-1}-\eta \frac{\sqrt{1-{\beta }_2^k}}{1-{\beta }_1^k}\frac{{\mathbf{m}}_k}{\sqrt{{\mathbf{v}}_k}+ϵ}\\ foreachvariation:({\mathbf{x}}_k{)}_i& \leftarrow ({\mathbf{x}}_{k-1}{)}_i-\eta \frac{\sqrt{1-{\beta }_2^k}}{1-{\beta }_1^k}\frac{({\mathbf{m}}_k{)}_i}{\sqrt{({\mathbf{v}}_k{)}_i}+ϵ}\end{array}$$

使用和调整优化器

优化器使用框架

以 Adam 为例，讲解优化器的使用框架。

torch.optim.Adam(params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,
                 weight_decay=0, amsgrad=False)

params,    # 待优化参数的iterable或定义了参数组的dict，通常为model.parameters()
lr=1e-3,     # 算法学习率，默认为0.001 
betas=(0.9, 0.999),    # 用于计算梯度以及梯度平方的运行平均值
eps=1e-8,    # 为了增加数值计算的稳定性而加到分母里的项
weight_decay=0,    # 权重衰减(L2惩罚)
amsgrad=False

建立测试网络，演示优化器的使用方式：

# 建立一个测试网络
class TestNet(nn.Module):
    def __init__(self):
        super(TestNet, self).__init__()    # 对继承自父类的属性进行初始化
        # 定义隐含层
        self.hidden = nn.Sequential(nn.Linear(13, 10),
                                    nn.ReLU(),)
        # 定义预测回归层
        self.regression = nn.Linear(10, 1)
    def forward(self, x):
        # 定义前向传播路径
        x = self.hidden(x)
        output = self.regression(x)
        return output

testnet = TestNet()    # 构建对象

# 使用迭代器(优化器)，为不同层定义统一的学习率
optimizer = optim.Adam(testnet.parameters(), lr = 0.001)

# 使用迭代器(优化器)，为不同层定义不同的学习率
optimizer = optim.Adam([{'params': testnet.hidden.parameters(), 'lr': 0.0001},
                        {'params': testnet.regression.parameters(), 'lr': 0.01}])

# 目标函数优化框架(非可正确运行实例)

# 定义损失函数为交叉熵(也可以定义其他的损失函数)
loss_function = nn.CrossEntropyLoss()  

for input, target in dataset:
    optimizer.zero_grad()    # 梯度清零
    output = TestNet(input)    # 计算预测值
    loss = loss_function(output, target)    # 计算梯度损失
    loss.backward()    # 损失反向传播
    optimizer.step()    # 更新梯度参数

学习率调整方式

optim.lr_scheduler 提供了几种优化器学习率的调整方式，先介绍一些常用的参数变量

last_epoch, # 用来设置何时开始调整学习率，=-1表示学习率设置为初始值
step_size, # 学习率会每经过step_size后调整为原来的gamma倍
milestones, # 使用一个列表来制定需要调整学习率的epoch数值, 调整为原来的gamma倍
T_max, # T_max个epoch后重新设置学习率
eta_min, # 每个周期的最小学习率

接下来是不同的学习率调整方式：

optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)
# last_epoch, 用来设置何时开始调整学习率，=-1表示学习率设置为初始值

不同的参数组设置不同的学习调整策略。

optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1)
# step_size, 学习率会每经过step_size后调整为原来的gamma倍
# gamma, 变化倍数

等间隔调整学习率，每经过 step_size 即成为原来的 gamma 倍。

optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1)
# milestones, 使用一个列表来制定需要调整学习率的epoch数值, 调整为原来的gamma倍
# gamma, 变化倍数

按照设定的间隔调整学习率。

optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1)
# gamma, 变化倍数

按照指数衰减调整学习率。

$$lr=lr\times {\gamma }^{epoch}$$

optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1)
# T_max, T_max个epoch后重新设置学习率
# eta_min 最小学习率(每个周期的最小学习率不会小于eta_min)

以余弦函数为周期，并在每个周期最大值时调整学习率。即 T_max 个 epoch 后重新设置学习率：
$${\eta }_t={\eta }_{\min }+\frac{1}{2}({\eta }_{\max }-{\eta }_{\max })(1+\cos (\frac{T_{cur}}{T_{\max }}\left)\right)$$

设置学习率调整方式的代码如下：

# 设置优化器
optimizer = optim.Adam(testnet.parameters(), lr = 0.001)
# 设置学习率调整方式
scheduler = optim.lr_scheduler.LambdaLR()

for epoch in range(epochs):
    for step, (b_x, b_y) in enumerate(train_dataloader): 
    	optimizer.zero_grad()    # 梯度清零
        output = TestNet(input)    # 计算预测值
        loss = loss_function(output, target)    # 计算梯度损失
        loss.backward()    # 损失反向传播
        optimizer.step()    # 更新梯度参数
    for step, (b_x, b_y) in enumerate(train_dataloader): 
    	pass
    scheduler.step()    # 更新学习率

损失函数

用来表示某次迭代中，预测值与实际验证集之间的差距程度。

最优化问题的目标就是将损失函数最小化。

torch.nn 模块提供了多种深度学习损失函数

nn.L1Loss(), # 平均绝对值误差损失，用于回归问题
nn.MSELoss(), # 均方误差损失，用于回归问题
nn.CrossEntropyLoss(), # 交叉熵损失，用于多分类
nn.NLLLoss(), # 负对数似然函数损失，用于多分类
nn.NLLLoss2d(), # 图片负对数似然函数损失，用于图像分割
nn.KLDivLoss(), # KL散度损失，用于回归问题
nn.BCELoss(), # 二分类交叉熵损失，用于二分类
nn.MarginRankingLoss(), # 评价相似度的损失
nn.MultiLabelMarginLoss(), # 多标签分类的损失
nn.SmoothL1Loss(), # 平滑的L1损失，用于回归问题
nn.SoftMarginLoss(), # 多标签二分类问题的损失

以交叉熵和均方误差为例

均方误差损失

$loss(x,y)=1/N\cdot (x_i-y_i{)}^2$

nn.MSELoss(size_average=None, reduce=None, reduction='mean')

size_average=None, # 计算的损失为每个batch的均值，否则为每个batch的和
reduce=None, # 计算的损失会根据size_average设定，试计算每个batch的均值或和
reduction='mean', # 'none', 'mean', 'sum' 来判断损失的计算方式，默认是均值

交叉熵损失

它将 LogSsoftMax 和 NLLLoss 集成到一个类中，一般用于多分配问题

nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100,
                 reduce=None, reduction='mean')

weight=None, # 是1维张量，包含n个元素，代表n类的权重，在训练样本不均衡时非常有用
ignore_index=-100, # 指定被忽略且对输入梯度没有贡献的目标值

当 weight = None

$$loss(x,class)=-\log \frac{\exp (x[class])}{{\sum }_{j}x[j]}=-x[class]+\log (\sum _j\exp (x[j]))$$

当 weight 被指定时

$$loss(x,class)=weight[class]\times (-x[class]+log(\sum _j\exp (x[j])\left)\right)$$

过拟合与欠拟合

考虑散点的欠拟合和过拟合问题。

信号和噪声：“信号”是数据中真正想要学习到的信息。“噪声”则是数据集中的不相关的信息和不确定性。好的机器学习模型应该提高信噪比。

拟合优度：模型预测值与真实值相匹配的程度。学习“噪声”的模型被称为是过拟合，在训练集上表现良好，但是与训练集的拟合优度差。欠拟合是对已有训练集的拟合程度就差，模型表现效果差，没有学习到数据中的信息。

过拟合指，在训练集上分类或预测过训练或者匹配，导致测试集上实际的分类和预测结果不理想。即只在训练集上损失较小，但是测试集上损失较大。

欠拟合指，模型还没能充分训练，在训练集上分类或预测不够匹配，误差较大，精度较小。

欠拟合曲线偏差较大，方差较小，过拟合的曲线偏差较小，方差较大。

模型评估

期望预测为：$\overline{f}(x)=E[f(x;D)]$ 。

期望泛化误差：表示为三个不同误差总和：偏差( bias)、方差(variance)、残差(irreducible error)。
$$\begin{array}{rl}f(x)& =w^{T}x,w服从正态分布\\ D& =[x_i,y_i{]}_{i=1}^n\\ & \\ E(f;D)& =E[(y-f(x;D){)}^2]\\ & =E[(f(x;D)-\overline{f}(x)+\overline{f}(x)-y_D{)}^2]\\ & =E[(f(x;D)-\overline{f}(x))]+E[(\overline{f}(x)-y_D{)}^2]\\ & =E[(f(x;D)-\overline{f}(x){)}^2]+E[(\overline{f}(x)-y+y-y_D)]\\ & =E[(f(x;D)-\overline{f}(x){)}^2]+E[(\overline{f}(x)-y{)}^2]+E[(y-y_D{)}^2]\\ & =var(x)+bia{s}^2(x)+{\epsilon }^2(x)\end{array}$$
偏差(bias)：期望输出与真实标记的差别，又错误的模型假设造成的，模型呈现欠拟合的状态。

方差(variance)：度量了同样大小的训练集变动所导致的学习性能的变化，即刻画了数据扰动造成的影响，模型呈现过拟合的状态。

噪声(残差 irreducible error)：数据本身存在的误差导致的学习困难。
$$\begin{gathered} 偏差(bias):bias=[\overline{f}(x)-y{]}^2 \\ 方差(variance):var(x)=E_D[f(x\cdot D)-\overline{f}(x{)}^2] \end{gathered}$$
理想情况下，应该在过拟合和欠拟合中做出权衡选择一个模型，使得模型在训练集上的表现量化同时也能准确对没有出现过的数据进行预测。

增加模型的复杂度会增加预测结果的方差同时减小偏差，相反减小模型复杂度会增加偏差、减小反差，这就是为什么被称为偏差和方差的权衡。

泛化能力：对未出现的数据进行预测的能力被称为模型的泛化能力。

预防

防止欠拟合：

选取或构造性的特征。

增加模型复杂度。

使用集成的方法。

增加模型训练时间。

监测过拟合：初始数据集分成单独的训练集和验证集，该方法可以近似我们的模型在新数据上的表现。

训练过程：训练集较小时训练误差远远小于验证误差，模型完全过拟合。训练集增大时，训练误差越来越接近验证误差，这时模型拟合效果较好。

防止过拟合：

1. 增加数据量。
2. 合理的数据切分。使用合理的比例切分训练集，验证集和测试集。
3. 正则化方法。即在损失函数上添加对训练参数的惩罚范数，对需要训练的参数进行约束。常用的参数有 $l_1$ 和 $l_2$ 范数(Ridge Regression / Lasso Regression)。
4. Dropout 。引入 Dropout 层，随机丢掉一些神经元，即让某几个神经元，以一定的概率 p 停止工作，减轻网络的过拟合现象。
5. 提前停止。当损失不再减小，或者精度不再增加时可以停止训练，但可能会导致参数训练不充分。
6. $k$ 折交叉验证选择训练参数
7. 删除部分相关度高的特征

网络参数初始化

为了得到高精度的训练结果，不使用默认参数初始化，而是使用一些特定的参数初始化方法。

常用初始化方法见教材，下面是参数初始化实例。

针对某一层的权重进行初始化

以一个卷积层为例

# 定义一个从3个特征映射到16个特征的卷积层
conv1 = nn.Conv2d(3, 16, 3)
# 使用标准正态分布初始化权重
torch.manual_seed(12)    # 随机数初始化种子
# 用生成的随机数代替张量conv1.weight的原始数据
nn.init.normal_(conv1.weight, mean=0, std=1)    
plt.figure(figsize=(8, 6))
plt.hist(conv1.weight.data.numpy().reshape((-1, 1)), bins=30)
plt.show()

​

​

# 使用指定值初始化偏置
# 让conv1的偏置参数中的每个元素，重新初始化为0.1
nn.init.constant_(conv1.bias, val=0.1)

Parameter containing:
tensor([0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000,
        0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000, 0.1000],
       requires_grad=True)

针对一个网络的权重初始化方法

对多层网络每个层的参数进行初始化

# 建立测试网络
class TestNet(nn.Module):
    def __init__(self):
        super(TestNet, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3)
        self.hidden = nn.Sequential(
            nn.Linear(1600, 100),
            nn.ReLU(),
            nn.Linear(100, 50),
            nn.ReLU()
        )
        self.cla = nn.Linear(50, 10)
        
    def forward(self, x):
        x = self.conv1(x)
        x = x.view(x.shape[0], -1)
        x = self.hidden(x)
        output = self.cla(x)
        return output

# 输出网络结构
from torchsummary import summary
testnet = TestNet()
summary(testnet, input_size=(3, 12, 12))

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 16, 10, 10]             448
            Linear-2                  [-1, 100]         160,100
              ReLU-3                  [-1, 100]               0
            Linear-4                   [-1, 50]           5,050
              ReLU-5                   [-1, 50]               0
            Linear-6                   [-1, 10]             510
================================================================
Total params: 166,108
Trainable params: 166,108
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.63
Estimated Total Size (MB): 0.65
----------------------------------------------------------------

print(testnet)

TestNet(
  (conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1))
  (hidden): Sequential(
    (0): Linear(in_features=1600, out_features=100, bias=True)
    (1): ReLU()
    (2): Linear(in_features=100, out_features=50, bias=True)
    (3): ReLU()
  )
  (cla): Linear(in_features=50, out_features=10, bias=True)
)

为什么上述 summary 写法是这样的呢？可以适当复习一下 torch.nn 章节和前面的网络参数计算章节。

首先我们设置了 conv1 的参数：$in\_channels=3,out\_channels=16,kernel\_size=3$ 。

对应到参数计算，即 $D_1=3,D_2=16$，滤波器大小为 $F\times F=3\times 3$。默认构造参数 $stride=1,padding=0$， 即 $S=1,P=0$

在 summary 方法中，$input\_size=D_1\times W_1\times H_1$。即卷积层输入数据的大小为 $W_1\times H_1\times D_1=12\times 12\times 3$

这些是已知量。

---

根据卷积层计算方法：
$$W_2=\frac{W_1-F+2P}{S}+1,H_2=\frac{H_1-F+2P}{S}+1,D_2=F$$
因此，$W_2=W_1-2,H_2=H_1-2$

输出 $W_2\times H_2\times D_2=(W_1-2)\times (H_1-2)\times F=10\times 10\times 16$，总共参数量为 $1600$。

然后我们开始设置全连接层 $linear2的参数:in\_channels=?,out\_channels=?$

前一层的输出等于后一层的输入，$in\_channels=1600$，$out\_channels$ 就根据需要输出类别的实际情况来确定了。

后面的全连接层类似。

---

以上都是题外话，然后我们来为上述网络的每一层定义进行权重初始化函数

def init_weights(m):
    # 如果是卷积层
    if type(m) == nn.Conv2d:
        torch.nn.init.normal_(m.weight, mean=0, std=0.5)    # 正态分布
    # 如果是全连接层
    if type(m) == nn.Linear:
        torch.nn.init.uniform_(m.weight, a=-0.1, b=0.1)    # -0.1-0.1均匀分布
        m.bias.data.fill_(0.01)    # 设置偏置bias为0.01

# 使用网络的apllu方法进行权重初始化
torch.manual_seed(13)    # 随机数初始化种子
testnet.apply(init_weights)

TestNet(
  (conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1))
  (hidden): Sequential(
    (0): Linear(in_features=1600, out_features=100, bias=True)
    (1): ReLU()
    (2): Linear(in_features=100, out_features=50, bias=True)
    (3): ReLU()
  )
  (cla): Linear(in_features=50, out_features=10, bias=True)
)