Matlab--优化工具箱

优化工具箱
优化工具箱（Optimization Toolbox）是对MATLAB数值计算环境扩展得一组函数，它包括以下最优化方法的内容：
1.无约束非线性最小化（Unconstrained nonlinear minimization）
2.有约束非线性最小化（Constrained nonlinear minimization）
3.二次规划和线性规划（Quadratic and linear programming）
4.最小二乘和曲线拟合（Nonlinear least squares and curve-fitting）
5.非线性系统的方程求解（Nonlinear system of equation solving）
6.有约束线性最小二乘（Constrained linear least squares）
所有功能都是M文件实现，你可以扩展这些函数。
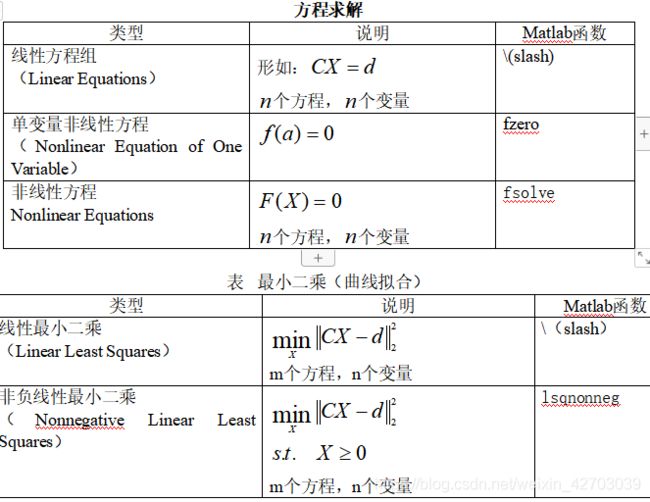
关于下表的变量说明：
在这里插入图片描述




一元非线性方程求根
语法：
x = fzero(fun,x0)
x = fzero(fun,x0,options)
x = fzero(fun,x0,options,P1,P2,…)
[x,fval] = fzero(…)
[x,fval,exitflag] = fzero(…)
[x,fval,exitflag,output] = fzero(…)
说明：
[X,FVAL,EXITFLAG,OUTPUT] = FZERO(FUN,X0,OPTIONS,P1,P2,…)
参数X0表示搜索的起点，一个函数可能有多个零点，但该命令只给出离X0最近的那个零点。
结构OPTIONS只有两个域：Display 和TolX。
输出参数EXITFLAG大于0表示找到了零点，小于0表示没有找到零点或者在搜索过程中遇到了无穷大的函数值。

例子：寻找函数sin(x)在3附近的零点
输入：x = fzero('sin',3)
输出：
x =
3.1416
例子：寻找函数在1到2之间的零点
输入：x = fzero('cos',[1 2])
输出：
x =
     1.5708
例子：解方程
方法1：编写一个M文件f.m
function y = f(x)
y = x.^3-2*x-5;
输入： 
z = fzero('f',2)
输出：
z =
2.0946
方法2：
输入：
f=inline(‘x.^3-2*x-5’,’x’)   %定义内联函数
z=fzero(f,2)
注意：2种定义函数在调用时的差异，一个有引号，一个没有引号。

非线性方程组求解
语法：
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
x = fsolve(fun,x0,options,P1,P2, … )
[x,fval] = fsolve(…)
[x,fval,exitflag] = fsolve(…)
[x,fval,exitflag,output] = fsolve(…)
[x,fval,exitflag,output,jacobian] = fsolve(…)
说明：
例子：求解方程组

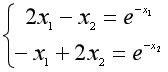
搜索起点： x0 = [-5 -5]
第一步：写一个M-文件计算在x处F：

function F = myfun(x)
F = [2*x(1) - x(2) - exp(-x(1));
      -x(1) + 2*x(2) - exp(-x(2))];

第二步：调用优化函数

x0 = [-5; -5];       % Make a starting guess at the solution
options=optimset('Display','iter');   % Option to display output
[x,fval] = fsolve('myfun',x0,options)    % call optimizer

第三步：输出结果

x =
    0.5671
    0.5671
fval =
   1.0e-08 *
    -0.5320
    -0.5320

无约束非线性最小化

fminbnd求单变量函数最小值点
fminbnd
语法：
x = fminbnd(fun,x1,x2)
x = fminbnd(fun,x1,x2,options)
x = fminbnd(fun,x1,x2,options,P1,P2,…)
[x,fval] = fminbnd(…)
[x,fval,exitflag] = fminbnd(…)
[x,fval,exitflag,output] = fminbnd(…)

说明：fminbnd用于求单变量函数的最小值点，它采用黄金分割查找和抛物线插值算法。
调用格式：
[X,FVAL,EXITFLAG,OUTPUT] = FMINBND(FUN,x1,x2,OPTIONS,P1,P2,…)
输入参数fun，x1，x2是必须的，其余参数允许缺省。fun为被计算的最小值点的单变量函数（目标函数）名的字符串，x1，x2为目标函数的自变量的取值范围。Fun可以为MATLAB系统内嵌的函数（如sin,cos等等），也可以为自定义函数。自定义函数可以通过MATLAB文件定义，也可以通过内联函数定义。
其它参数：P1，P2，…是向目标函数传递的附加参数；options是一个结构型的变量，用于指定优化参数，可通过optimset函数设置。
目标函数内嵌函数：
求解模型
使用命令：

[x,fval]=fminbnd('cos(4*x+5)',0,pi/2)
x1=0:0.1:pi/2;
plot(x1,cos(4*x1+5))
运行结果：
Optimization terminated successfully:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-004 
x =
    1.1062
fval =
   -1.0000

表示当x=1.1062时，函数取得最小值-1。
目标函数为非内嵌函数：
比如求解模型：
将上述问题转化为求模型：该模型的最小值点，也就是原模型的最大值点。

方法1：采用m文件定义函数
function fx=funmin1(x)
fx=-(x.*x.*x-8*x-15*x.*x);
输入命令：[x,fval]=fminbnd('funmin1',-10,10)
得到如下结果：
Optimization terminated successfully:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-004 
x =
   -0.2599
fval =
   -1.0484
所以原模型中当x＝-0.2599时，取得最大值1.0484。
可以将这里的结果与解析结果比较。
方法2：采用内联函数
定义内联函数用inline。
输入命令：
f=inline('-(x.*x.*x -15*x.*x-8*x)')
[x,fval]=fminbnd(f,-10,10)
输出结果：
f =
     Inline function:
     f(x) = -(x.*x.*x-8*x-15*x.*x)

Optimization terminated successfully:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-004 
x =
   -0.2599

fval =
   -1.0484

fminunc
语法：
x = fminunc(fun,x0)
x = fminunc(fun,x0,options)
x = fminunc(fun,x0,options,P1,P2,…)
[x,fval] = fminunc(…)
[x,fval,exitflag] = fminunc(…)
[x,fval,exitflag,output] = fminunc(…)
[x,fval,exitflag,output,grad] = fminunc(…)
[x,fval,exitflag,output,grad,hessian] = fminunc(…)
说明：
例子：求函数f(x) = sin(x) + 3 的最小值
函数f(x)采用内联函数定义。
输入：
f = inline(‘sin(x)+3’);
x = fminunc(f,4)
输出结果：
x =
4.7124
fminsearch求多变量函数最小值点
命令：fminsearch函数用于求多变量函数的最小值点，它采用Neder-Mead单纯形算法。
调用格式：
[X,FVAL,EXITFLAG,OUTPUT] = fminsearch (FUN,X0,OPTIONS,P1,P2,…)
必须的参数为：FUN和X0。
此调用的大部分参数意义与fminbnd相同。
x0是最小值点的初始值，这一般由用户自己根据实际确定，也可猜测。
这里的结构options的域比函数fminbnd多一个：TolFun，指终止计算的目标函数的容差值。
退出标志EXITFLAG，也比函数fminbnd增加一种情况：小于0表示目标函数不收敛。

举例：设目前建立了下面的无约束最优化模型
从理论上该目标函数的最小值点在（1，3）处取得。
编写目标函数程序文件，这里命名为fun2x.m：

function y=fun2x(x)

%此模型的目标函数，注意x为向量，其元素依次对应于x1,x2,…；
%这里对应于x1,x2。
y= 2*(x(1)-1)^2+3*(x(2)-3)2;

在命令行输入：

[x,funminvalue,exitflag]=fminsearch(‘fun2x’,zeros(1,2))
输入结果如下：
Optimization terminated successfully:
x =
    1.0000    3.0000
funminvalue =
  3.1076e-009
exitflag =
     1

由结果输出，可见目标函数在(1,3)处取得最小值。退出标志exitflag=1表示找到最小值点，搜索成功。
有约束非线性最小化fmincon
求解非线性规划问题的Matlab函数。
（有关fmincon的使用例子可以参考高速公路问题的模型求解）
fmincon函数求解形如下面的有约束非线性规划模型。约束中可以有等式约束。
(可以含线性、非线性约束均可)

语法：
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2, …)
[x,fval] = fmincon(…)
[x,fval,exitflag] = fmincon(…)
[x,fval,exitflag,output] = fmincon(…)
[x,fval,exitflag,output,lambda] = fmincon(…)
[x,fval,exitflag,output,lambda,grad] = fmincon(…)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(…)
例1：求解如下规划问题。

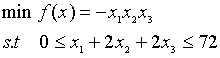
第一步：编写一个M文件返回目标函数在点处的值。
第一步：编写一个M文件返回目标函数f在点x处的值。
function f = myfun(x)
f = -x(1) * x(2) * x(3);

第二步：为了调用MATLAB函数，必须将模型中的约束转化为如下形式。

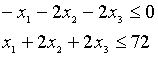
这是2个线性约束，形如，
这里：
A=[-1 -2 -2; 1 2 2 ];
b=[0 72]’;

第三步：提供一个搜索起点，然后调用相应函数，程序如下：

x0 = [10; 10; 10]; % Starting guess at the solution
[x,fval] = fmincon(‘myfun’,x0,A,b)

最后得到如下结果：
x =
24.0000
12.0000
12.0000

此时目标函数值为：
fval =
-3.4560e+03
其中线性非等式约束（Ax<=b）的结果如下：
A*x-b=
-72
0
可见满足模型约束要求。

线性规划linprog
函数：linprog
求解如下线性规划模型：

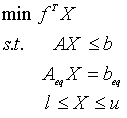
语法：
x = linprog(f,A,b,Aeq,beq)
x = linprog(f,A,b,Aeq,beq,lb,ub)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval] = linprog(…)
[x,fval,exitflag] = linprog(…)
[x,fval,exitflag,output] = linprog(…)
[x,fval,exitflag,output,lambda] = linprog(…)
输入参数：
f 目标函数费用系数向量
A
B
exitflag
> 0 成功找到最优解
0 达到最大迭代次数也没有找到最优解
< 0 该线性规划问题不可行或者linprog计算失败
边界设置lb,ub
如果x(i)无边界，则lb(i)=-Inf,ub(i)=Inf

例1：求解如下线性规划模型
目标函数：
约束条件：

第一步：根据模型和语法输入有关系数

f = [-5; -4; -6]
A =  [1 -1  1
      3  2  4
      3  2  0];
b = [20; 42; 30];
lb = zeros(3,1);

第二步：编写调用程序
[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);

第三步：输入x，fval，lambda.ineqlin，和lambda.lower得到如下结果：
x = 
     0.0000
    15.0000
3.0000
fval =
  -78.0000

lambda.ineqlin =
     0
     1.5000
0.5000
lambda.lower =
     1.0000
     0
0
结果说明：当x1=0，x2=15，x3=3时，目标函数 f 取得最小值-78。

最小二乘和曲线拟合
线性最小二乘
适合如下模型：

语法：C=MLDIVIDE(A,B) 等价于C=A\B
（1）如果A是方阵，B是列向量，则其表示求解方程组A*X=B,结果是X=A\B即Inv(A)*B
（2）如果A不是方阵，则表示用最小二乘法求解模型

有m组样本，即已知
求向量a满足上式。
Matlab求解方法：
构造矩阵

非线性曲线拟合lsqcurvefit
解决最小二乘意义下的非线性曲线拟合问题。
这类问题的模型如下：

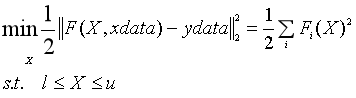
语法：
x = lsqcurvefit(fun,x0,xdata,ydata)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options,P1,P2,…)
[x,resnorm] = lsqcurvefit(…)
[x,resnorm,residual] = lsqcurvefit(…)
[x,resnorm,residual,exitflag] = lsqcurvefit(…)
[x,resnorm,residual,exitflag,output] = lsqcurvefit(…)
[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(…)
[x,resnorm,residual,exitflag,output,lambda,jacobian] =
lsqcurvefit(…)

例1：
向量数据xdata和ydata长度均为n，求系数 满足下列方程：

也就是求解如下的规划模型：

其中F(x,xdata) = x(1)*xdata.^2+ x(2)*sin(xdata) + x(3)*xdata.^3,起点x0 = [0.3, 0.4, 0.1]。

第一步：编写F函数的M文件：
function F = myfun(x,xdata)
F = x(1)*xdata.^2 + x(2)*sin(xdata) + x(3)*xdata.^3;

第二步：调用优化程序
% xdata 和 ydata 是用实验方法得到的数据

xdata = [3.6 7.7 9.3 4.1 8.6 2.8 1.3 7.9 10.0 5.4];
ydata = [16.5 150.6 263.1 24.7 208.5 9.9 2.7 163.9 325.0 54.3];
x0 = [10, 10, 10]                    % Starting guess
[x,resnorm] = lsqcurvefit('myfun',x0,xdata,ydata)

注意：xdata和ydata必须有相同的长度。
经过 33 次函数计算，得到如下结果：

x = 
0.2269    0.3385    0.3021
% residual or sum of squares
resnorm = 
     6.2950