ONLINE CORESET SELECTION FOR REHEARSAL-BASED CONTINUAL LEARNING 论文阅读+代码解析
本篇依旧是针对持续学习的工作,也是FedWEIT的团队进行的研究,论文地址点这里
一. 介绍(简单描述)
在持续学习中为了应对灾难性遗忘,常见的方法有基于正则化、基于记忆重塑以及基于动态架构。其中基于记忆重塑能通过保存少量旧样本而达到一个很好的准确率,因此被广泛地使用。但是,很多方法选取的样本是随机选取,就导致了可能存在样本重复、噪音等问题,如下图:
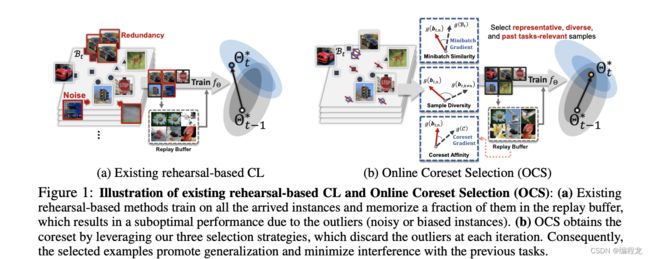
二. 基于记忆重塑的持续学习
在持续学习中,存在一系列的任务 { T 1 , . . . , T T } = T \{\mathcal{T_1,...,T}_T\}=\mathcal{T} {T1,...,TT}=T,其中每个任务数据可以表示为 D t = { x t , n , y t , n } n = 1 N t ∼ X t × Y t \mathcal{D}_t=\{x_{t,n},y_{t,n}\}^{N_t}_{n=1} ∼ \mathcal{X}_t×\mathcal{Y}_t Dt={xt,n,yt,n}n=1Nt∼Xt×Yt,其中 N t N_t Nt表示当前任务的所有数据实例,而 X t × Y t \mathcal{X}_t×\mathcal{Y}_t Xt×Yt表示的是当前任务自己的分布(我们不知道)。假设不同的任务的标签都不相同 y t ∩ y k = ∅ , ∀ t ≠ k y_t \cap y_k=\empty ,\forall t \not = k yt∩yk=∅,∀t=k,同时,过去的数据不会在未来出现。设 f Θ : X 1 : t → Y 1 : t f_{\Theta}:\mathcal{X}_{1:t}\rightarrow\mathcal{Y}_{1:t} fΘ:X1:t→Y1:t为网络函数,则我们的在任务 t t t的优化目标为:
min Θ ∑ n = 1 N t ℓ ( f Θ ( x t , n ) , y t , n ) \min_{\Theta}\sum_{n=1}^{N_t}\ell(f_{\Theta}(x_{t,n}),y_{t,n}) Θminn=1∑Ntℓ(fΘ(xt,n),yt,n)
这里 ℓ ( . ) \ell(.) ℓ(.)表示的是一个标准的损失函数。为了应对灾难性遗忘,基于记忆重塑的方法会为每个任务开辟一个缓存区: C k = { x k , j , y k , j } j = 1 J k ∼ D k , ∀ k < t and J k ≪ N k \mathcal{C}_k=\{x_{k,j},y_{k,j}\}^{J_k}_{j=1} ∼ \mathcal{D}_k, \forall k \lt t \text{ and } J_k \ll N_k Ck={xk,j,yk,j}j=1Jk∼Dk,∀k<t and Jk≪Nk。而选取的样本则是随机的,而为了能够在每个任务中找到典型的样本,本文的目标是选择能够促进当前任务适应的数据实例,同时最小化对先前任务的灾难性遗忘。因此提出了一个选择准则,该准则可以选择最大化代表实例和当前任务数据集之间梯度相似性的子集,具体来说,如下:
u ∗ = maximize u ∈ N κ S ( 1 N t ∇ f Θ ( D t ) , 1 κ ∑ n ∈ u ∇ f Θ ( x t , n , y t , n ) ) , where u = { n : n ∈ N < N t } \mathbf{u}^*=\underset{\mathbf{u} \in \mathbb{N}^\kappa}{\operatorname{maximize}} \mathcal{S}\left(\frac{1}{N_t} \nabla f_{\Theta}\left(\mathcal{D}_t\right), \frac{1}{\kappa} \sum_{n \in \mathbf{u}} \nabla f_{\Theta}\left(\boldsymbol{x}_{t, n}, y_{t, n}\right)\right), \quad \text { where } \mathbf{u}=\left\{n: n \in \mathbb{N}_{
其中 S \mathcal{S} S表示相似函数而 u ∗ \mathbf{u}^* u∗则表示为选择的top- κ \kappa κ个样本。然而,从整个数据集中获取一个代表性的子集对于在线持续学习来说是非常昂贵和困难的,因此,下面将一个小批次视为数据集的近似值,并在每个小批次迭代中选择几个具有代表性的数据实例。
三. ONLINE CORESET SELECTION
定义 1 (Minibatch similarity) 让 b t , n = { x t , n , y t , n } ∈ B t \boldsymbol{b}_{t, n}=\left\{\boldsymbol{x}_{t, n}, y_{t, n}\right\} \in \mathcal{B}_t bt,n={xt,n,yt,n}∈Bt 提供在第 t t t个任务的第 n n n个数据的梯度为: ∇ f Θ ( b t , n ) \nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) ∇fΘ(bt,n) 。 让 ∇ ˉ f Θ ( B t ) \bar{\nabla} f_{\Theta}\left(\mathcal{B}_t\right) ∇ˉfΘ(Bt)表示为一个batch的平均梯度 B t \mathcal{B}_t Bt. 那么minibatch similarity S ( b t , n ∣ B t ) \mathcal{S}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_t\right) S(bt,n∣Bt) 表示为:
S ( b t , n ∣ B t ) = ∇ f Θ ( b t , n ) ∇ ˉ f Θ ( B t ) ⊤ ∥ ∇ f Θ ( b t , n ) ∥ ⋅ ∥ ∇ ˉ f Θ ( B t ) ∥ \mathcal{S}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_t\right)=\frac{\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) \bar{\nabla} f_{\Theta}\left(\mathcal{B}_t\right)^{\top}}{\left\|\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right)\right\| \cdot\left\|\bar{\nabla} f_{\Theta}\left(\mathcal{B}_t\right)\right\|} S(bt,n∣Bt)=∥∇fΘ(bt,n)∥⋅∥ ∥∇ˉfΘ(Bt)∥ ∥∇fΘ(bt,n)∇ˉfΘ(Bt)⊤
定义 2(Sample diversity) 让 b t , n = { x t , n , y t , n } ∈ B t \boldsymbol{b}_{t, n}=\left\{\boldsymbol{x}_{t, n}, y_{t, n}\right\} \in \mathcal{B}_t bt,n={xt,n,yt,n}∈Bt 提供在第 t t t个任务的第 n n n个数据的梯度为: ∇ f Θ ( b t , n ) \nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) ∇fΘ(bt,n) 。那么Sample diversity V ( b t , n ∣ B t \ b t , n ) \mathcal{V}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{t \backslash \boldsymbol{b}_{t, n}}\right) V(bt,n∣Bt\bt,n)表示为:
V ( b t , n ∣ B t \ b t , n ) = − 1 N t − 1 ∑ p ≠ n N t − 1 ∇ f Θ ( b t , n ) ∇ f Θ ( b t , p ) ⊤ ∥ ∇ f Θ ( b t , n ) ∥ ⋅ ∥ ∇ f Θ ( b t , p ) ∥ \mathcal{V}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{t \backslash \boldsymbol{b}_{t, n}}\right)=\frac{-1}{N_t-1} \sum_{p \neq n}^{N_t-1} \frac{\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) \nabla f_{\Theta}\left(\boldsymbol{b}_{t, p}\right)^{\top}}{\left\|\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right)\right\| \cdot\left\|\nabla f_{\Theta}\left(\boldsymbol{b}_{t, p}\right)\right\|} V(bt,n∣Bt\bt,n)=Nt−1−1p=n∑Nt−1∥∇fΘ(bt,n)∥⋅∥∇fΘ(bt,p)∥∇fΘ(bt,n)∇fΘ(bt,p)⊤
可以发现第一个 (Minibatch similarity)表示的是一个batch哪一个图片最能体现出这个batch的信息(也就是越接近这个batch的中心);而第二个(Sample diversity)则是去看选择的样本多样性问题,也就是尽量保证存下的这些样本之间差异最大(因此要乘一个负号)。
3.1 ONLINE CORESET SELECTION FOR CURRENT TASK ADAPTATION
经过上述的定义之后,可以将两者结合起来进行样本的选择,如下:
u ∗ = { argmax n ( κ ) S ( b t , n ∣ B t ) + V ( b t , n ∣ B t ∣ b t , n ) ∣ n ∈ { 0 , … , ∣ B t ∣ − 1 } } . \mathbf{u}^*=\left\{\underset{n}{\operatorname{argmax}}(\kappa) \ \mathcal{S}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_t\right)+\mathcal{V}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{t \mid \boldsymbol{b}_{t, n}}\right) \mid n \in\left\{0, \ldots,\left|\mathcal{B}_t\right|-1\right\}\right\} . u∗={nargmax(κ) S(bt,n∣Bt)+V(bt,n∣Bt∣bt,n)∣n∈{0,…,∣Bt∣−1}}.
经过不断的迭代,最终可以选择出top- κ \kappa κ个样本。一旦选择了具有代表性的核心集,就可以在每次迭代中为当前任务优化以下目标:
minimize Θ 1 κ ∑ ( x ^ y ^ ^ ) ∈ B ^ t κ ℓ ( f Θ ( x ^ ) , y ^ ) , where B ^ t = B t [ u ∗ ] \underset{\Theta}{\operatorname{minimize}} \frac{1}{\kappa} \sum_{(\hat{\boldsymbol{x}} \hat{\hat{y}}) \in \widehat{\mathcal{B}}_t}^\kappa \ell\left(f_{\Theta}(\hat{\boldsymbol{x}}), \hat{y}\right), \quad \text { where } \widehat{\mathcal{B}}_t=\mathcal{B}_t\left[\mathbf{u}^*\right] Θminimizeκ1(x^y^^)∈B t∑κℓ(fΘ(x^),y^), where B t=Bt[u∗]
最后将每次迭代中选定的核心集视为回放缓冲区的候选。在完成每个任务训练后,我们在收集的候选对象中选择一个核心集 C t \mathcal{C}_t Ct,或者也可以迭代更新 C t \mathcal{C}_t Ct,以保持有限的缓冲区大小,以便继续学习。
3.2 ONLINE CORESET SELECTION FOR CONTINUAL LEARNING
定义 3(Coreset affinity) 让 b t , n = { x t , n , y t , n } ∈ B t \boldsymbol{b}_{t, n}=\left\{\boldsymbol{x}_{t, n}, y_{t, n}\right\} \in \mathcal{B}_t bt,n={xt,n,yt,n}∈Bt 提供在第 t t t个任务的第 n n n个数据的梯度为: ∇ f Θ ( b t , n ) \nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) ∇fΘ(bt,n) 。同时 ∇ ˉ f Θ ( B C ) \bar{\nabla} f_{\Theta}\left(\mathcal{B}_{\mathcal{C}}\right) ∇ˉfΘ(BC)表示为从缓存区 C \mathcal{C} C中随机选的batch的样本的平均梯度,那么Coreset affinity A ( b t , n ∣ B C ∼ C ) \mathcal{A}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{\mathcal{C}} \sim \mathcal{C}\right) A(bt,n∣BC∼C)表示为:
A ( b t , n ∣ B C ∼ C ) = ∇ f Θ ( b t , n ) ∇ ˉ f Θ ( B C ) ⊤ ∥ ∇ f Θ ( b t , n ) ∥ ⋅ ∥ ∇ ˉ f Θ ( B C ) ∥ \mathcal{A}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{\mathcal{C}} \sim \mathcal{C}\right)=\frac{\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right) \bar{\nabla} f_{\Theta}\left(\mathcal{B}_{\mathcal{C}}\right)^{\top}}{\left\|\nabla f_{\Theta}\left(\boldsymbol{b}_{t, n}\right)\right\| \cdot\left\|\bar{\nabla} f_{\Theta}\left(\mathcal{B}_{\mathcal{C}}\right)\right\|} A(bt,n∣BC∼C)=∥∇fΘ(bt,n)∥⋅∥ ∥∇ˉfΘ(BC)∥ ∥∇fΘ(bt,n)∇ˉfΘ(BC)⊤
这一部分是为了能够保证当前的样本和从缓存区里面选的样本比较亲和(也就是相近),这是因为能够保证这个样本不会过多的损害之前的任务,能够代表更多的过去任务信息。因此,我们的选择目标变为:
u ∗ = { argmax n ( κ ) S ( b t , n ∣ B t ) + V ( b t , n ∣ B t ∣ b t , n ) + τ A ( b t , n ∣ B C ) ∣ n ∈ { 0 , … , ∣ B t ∣ − 1 } } \mathbf{u}^*=\left\{\underset{n}{\operatorname{argmax}}(\kappa) \mathcal{S}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_t\right)+\mathcal{V}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{t \mid \boldsymbol{b}_{t, n}}\right)+\tau \mathcal{A}\left(\boldsymbol{b}_{t, n} \mid \mathcal{B}_{\mathcal{C}}\right) \mid n \in\left\{0, \ldots,\left|\mathcal{B}_t\right|-1\right\}\right\} u∗={nargmax(κ)S(bt,n∣Bt)+V(bt,n∣Bt∣bt,n)+τA(bt,n∣BC)∣n∈{0,…,∣Bt∣−1}}
其中 τ \tau τ为超参数。因此,经过上述的选择后搭配上从缓存区 C \mathcal{C} C获得的样本后,我们就可以用来进行训练,损失优化如下:
minimize Θ 1 κ ∑ ( x ^ , y ^ ) ∈ B ^ t κ ℓ ( f Θ ( x ^ ) , y ^ ) + λ ∣ B C ∣ ∑ ( x , y ) ∈ B C ∣ B C ∣ ℓ ( f Θ ( x ) , y ) \underset{\Theta}{\operatorname{minimize}} \frac{1}{\kappa} \sum_{(\hat{\boldsymbol{x}}, \hat{y}) \in \widehat{\mathcal{B}}_t}^\kappa \ell\left(f_{\Theta}(\hat{\boldsymbol{x}}), \hat{y}\right)+\frac{\lambda}{\left|\mathcal{B}_{\mathcal{C}}\right|} \sum_{(\boldsymbol{x}, y) \in \mathcal{B}_{\mathcal{C}}}^{\left|\mathcal{B}_{\mathcal{C}}\right|} \ell\left(f_{\Theta}(\boldsymbol{x}), y\right) Θminimizeκ1(x^,y^)∈B t∑κℓ(fΘ(x^),y^)+∣BC∣λ(x,y)∈BC∑∣BC∣ℓ(fΘ(x),y)
其中 B ^ t = B t [ u ∗ ] \widehat{\mathcal{B}}_t=\mathcal{B}_t\left[\mathbf{u}^*\right] B t=Bt[u∗]。最后,算法过程如下:

总结一下:其实就是在每一个batch到来时,我们按照上述的标准去计算出核心的集合,然后再利用选择的核心样本+过去随机的样本去更新参数,最后就是存的时候再一次进行判断,放到缓冲区行程过去的样本。
四. 代码解析
本文的代码链接点这里
本文的核心就是设计了一个选择样本的标准,我们着重看这里就行:

这里个g代表的是一个batch的平均梯度,eg表示每个batch中每个样本自己的梯度,也就是eg=[eg1,eg2,…],相当于就是一个tensor就直接包括了所有的部分。可以发现上述的三个标准基本都是利用了向量的夹角计算公式,所以首先使用torch.norm去求解长度(也就是求解第二范式),mean_sim就可以根据g和eg进行计算。再来就是arg_div是第二个标准,他这里是要求每一个样本和其他样本进行比对,选差异最大的,这里为了方便计算不把自身排除,因为自身和自身梯度一样也是在最后一名不影响整体的排序,最后再进行平均。而第三个标准则根据旧任务的梯度来进行判断即可,最后measure就是算出来的具体值,注意这里的measure也是多个值组成,即measure=[measure1,measure2…],相当于包括了所有样本根据三个标准计算出来的值,最后在进行排序即可选出最大的前几个。