动手实现深度神经网络7 实现CNN
动手实现深度神经网络7 实现CNN
经过了之前的学习,我们已经掌握了如何构造、优化和使用一个深度神经网络了。然而,单纯的深度神经网络无法考虑到图像中相邻像素中可能存在的联系。于是,这里我们将实现一种专门针对图像处理的卷积神将网络CNN。
关于CNN的理论知识我之前的文章有详细的讲述:Python深度学习入门笔记 4 CNN。这里我们依据不再赘述,直接展示代码中可能会遇到的问题。
卷积层的实现
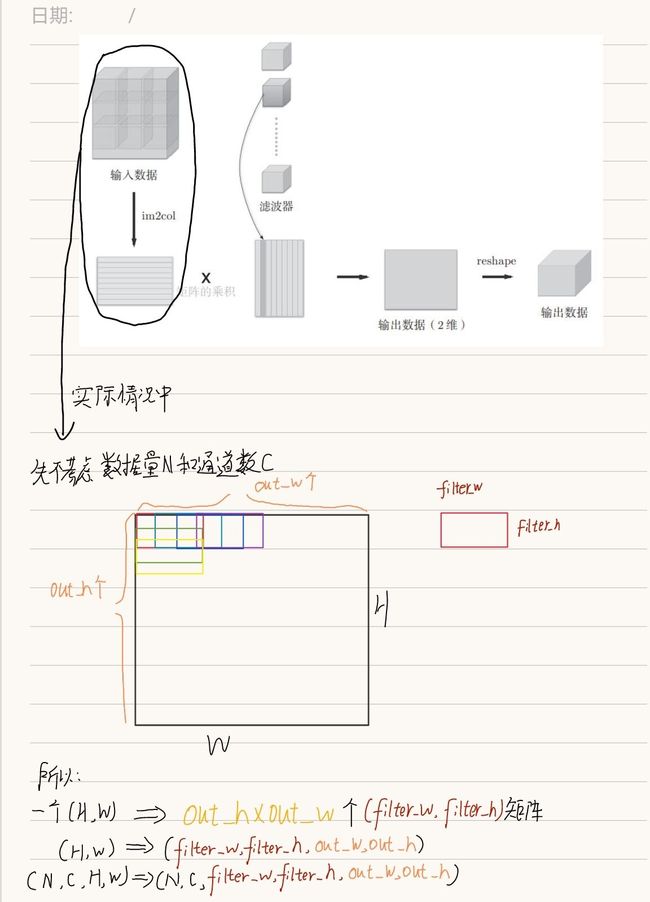
CNN中处理的是4维数据(batch_num, channel, height, width),因此卷积运算的实现看上去会很复杂,但是通过im2col,问题就会变得很简单。
im2col是一个函数,将输入数据展开以适合滤波器(权重)。对每个3维的输入数据应用im2col后,数据转换为2维矩阵(正确地讲,是把包含批数量的4维数据转换成了2维数据)。
![]()
使用im2col展开后,展开后的元素个数会多于原方块的元素个数。因此,使用im2col的实现存在比普通的实现消耗更多内存的缺点。但是,汇总成一个大的矩阵进行计算,对计算机的计算颇有益处。比如,在矩阵计算的库(线性代数库)等中,矩阵计算的实现已被高度最优化,可以高速地进行大矩阵的乘法运算。因此,通过归结到矩阵计算上,可以有效地利用线性代数库。
im2col和col2im的实现
col2im是im2col的逆过程。
代码中需要注意的地方我是用!标注,然后会在下面进行说明。
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
filter_h : 滤波器的高
filter_w : 滤波器的长
stride : 步幅
pad : 填充
Returns
-------
col : 2维数组
"""
N, C, H, W = input_data.shape
# 计算输出的大小
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
# np.pad用于填充
# 第一个参数是填充的数组
# 第二个参数是一个列表,表示各个轴填充的个数:
# 例如[(1,2),(0,0)]表示 第一个轴上,前面填充1个,后面填充2个 第二个轴上 前面填充0个,后面填充0个
# 第三个参数是填充的模式,默认是'constant'常数填充,默认是0,可以通过constant_values = (0,0)这样设置。
#具体到这里,因为第一个轴是数据量,第二个周是通道数,所以不填充,第三第四个轴是高和长,才根据输入进行填充
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
# 一 !!!!!!!!!
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
# 二 !!!!!!!!!!
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
# 三 !!!!!!!!!!
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_shape : 输入数据的形状(例:(10, 1, 28, 28))
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
一!!!!!!!!!
这里生成一个六维0矩阵,我们来说明一下。首先把“数据量N”和“通道数C”摘出来不考虑,因为要把二维矩阵转换为一个适合与卷积相乘的形状,所以一个(H*W)的矩阵,要暂时看成out_h*out_w个(ilter_h,filter_w)形状的矩阵,也就是一个(filter_h, filter_w, out_h, out_w)的四维矩阵。
二!!!!!!!!!
这里是将img中的数据对应复制到六维矩阵col中。实际上是每次将每个(ilter_h,filter_w)矩阵中的1一个像素复制到col中。
三!!!!!!!!!
这里将col转换为最终需要的(N*out_h*out_w, C*filter_h*filter_w)的矩阵。
卷积层代码
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中间数据(backward时使用)
self.x = None
self.col = None
self.col_W = None
# 权重和偏置参数的梯度
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
#1
self.db = np.sum(dout, axis=0)
#2
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
#3
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
卷积层也是和之前的层一样,提供正向传播和反向传播两个方法。经过img2col之后,可以使用np.dot(col, col_W) + self.b计算卷积,而这个计算形式与之前介绍的Affine层是一样的,因此,正向传播和反向传播的流程也是一样的。代码中的123是反向传播的运算,如果感觉很陌生可以回到这里再复习一下。反向传播是最后用到col2im,它是im2col的逆过程。
池化层的实现
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h * self.pool_w)
# 记录最大值的下表==下标,反向传播时要用到
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
# flatten把多维数组扁平化为一维数组
# 反向传播时,arg_max对应位置设置为dout对应的值,其他位置为0
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
池化层是反向传播与Relu的反向传播类似,基本思想都是保存正向传播时“通过(选取)”的下标,在反向传播时只“放行”对应位置的值,其他位置的值设为0。
一个CNN的实现
组成CNN的基本组件已经有了,像之前一样把各个层拼接在一起就可以啦!
“conv - relu - pool - affine - relu - affine - softmax”
class SimpleConvNet:
"""简单的ConvNet
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 输入大小(MNIST的情况下为784)
hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100])
output_size : 输出大小(MNIST的情况下为10)
activation : 'relu' or 'sigmoid'
weight_init_std : 指定权重的标准差(e.g. 0.01)
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
Trainer
在使用这个CNN之前,我们要介绍神经网络中的另一个角色Trainer,它和之前介绍的optimizer一样,都是将神经网络中的一部分独立于具体神经网络独立于训练数据的功能抽取出来,封装成一个类。
具体来说Trainer像是神经网络训练过程的“操作员”,我们把(具体的网络实例(对象),数据,超参数,optimizer实例)这些当做参数传递给Trainer,Trainer会替我们完成剩下的所有工作。
Trainer是通用的,写好一个Trainer之后可以在任何场景,使用任何网络处理任何数据时使用。
class Trainer:
"""进行神经网络的训练的类
"""
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr':0.01},
evaluate_sample_num_per_epoch=None, verbose=True):
self.network = network
self.verbose = verbose
self.x_train = x_train
self.t_train = t_train
self.x_test = x_test
self.t_test = t_test
self.epochs = epochs
self.batch_size = mini_batch_size
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
# optimzer
optimizer_class_dict = {'sgd':SGD, 'momentum':Momentum, 'nesterov':Nesterov,
'adagrad':AdaGrad, 'rmsprpo':RMSprop, 'adam':Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)
self.train_size = x_train.shape[0]
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
self.max_iter = int(epochs * self.iter_per_epoch)
self.current_iter = 0
self.current_epoch = 0
self.train_loss_list = []
self.train_acc_list = []
self.test_acc_list = []
def train_step(self):
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
grads = self.network.gradient(x_batch, t_batch)
self.optimizer.update(self.network.params, grads)
loss = self.network.loss(x_batch, t_batch)
self.train_loss_list.append(loss)
if self.verbose: print("train loss:" + str(loss))
if self.current_iter % self.iter_per_epoch == 0:
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print("=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc) + " ===")
self.current_iter += 1
def train(self):
for i in range(self.max_iter):
self.train_step()
test_acc = self.network.accuracy(self.x_test, self.t_test)
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))
可以看到,Trainer并不神秘,其中大多数都是我们之前写过的代码,Trainer只是把它们封装在一个完整的通用的流程里。
使用Trainer训练
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 处理花费时间较长的情况下减少数据
#x_train, t_train = x_train[:5000], t_train[:5000]
#x_test, t_test = x_test[:1000], t_test[:1000]
max_epochs = 20
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 保存参数
network.save_params("params.pkl")
print("Saved Network Parameters!")
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
可以看到,到现在,我们的神经网络非常优雅:
-
几个层拼接成一个网络
-
把网络和一些超参数等传递给Trainer
-
Trainer.train()
每一步都非常的规范、流畅和易于扩展。