机器学习之降维算法：主成分分析（PCA）

1. PCA理论

解决过拟合问题常见思路：增加训练处理数据、加入正则化项、对特征进行降维。
降维方法：直接进行特征选择、线性降维（PCA，MDS）、非线性降维（流形）。

1.1 高维样本均值和方差表示

给定数据Data矩阵，$X=(x_1,x_2,...,x_N{)}_{N\ast p}^T$。
样本特征均值：$${\overline{X}}_{p\ast 1}=\frac{1}{N}\sum _{i=1}^N{x}_i$$
样本特征方差：$$S_{p\ast p}=\frac{1}{N}\sum _{i=1}^N(x_i-\overline{X})(x_i-\overline{X}{)}^T$$
则有高维样本均值和方差的表示：

${\overline{X}}_{p\ast 1}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$
$=\frac{1}{N}(x_1,x_2,...,x_N){\left(\begin{array}{c}1\\ ...\\ 1\end{array}\right)}_{N\ast 1}$
$=\frac{1}{N}{X}^T{1}_{N\ast 1}$

$S_{p\ast p}=\frac{1}{N}{\sum }_{i=1}^N(x_i-\overline{X})(x_i-\overline{X}{)}^T$
$=\frac{1}{N}(x_1-\overline{X},...,x_N-\overline{X}){\left(\begin{array}{c}(x_1-\overline{X}{)}^T\\ ...\\ (x_N-\overline{X}{)}^T\end{array}\right)}_{N\ast 1}$
$=\frac{1}{N}{X}^T(I_N-\frac{1}{N}{1}_N{1}_N^T)N{X}^T(I_N-\frac{1}{N}{1}_N{1}_N^T{)}^{T}X$
将括号里的表达式看成H，则有：
$=\frac{1}{N}{X}^{T}H{H}^{T}X$
可以尝试计算会发现：
$H^T=H$
$H^n=H$
则有：
$S_{p\ast p}=\frac{1}{N}{X}^{T}HX$

1.2 最大投影方差&最小重构距离

classical PCA可以看成：
一个中心：原始特征空间的重构（使得特征从相关$\to$无关）；
两个基本点：1. 最大投影方差 2. 最小重构距离

基本思想是将原始特征在一个方向上进行投影，思想和LDA线性判别分析有点像但是有区别，若有相关问题需要温故LDA就再写一篇LDA的笔记。使得在样本特征在投影方向上得到的新样本方差最大，且使得新样本数据能够区分，重构回去的可能性尽可能大。如图所示：

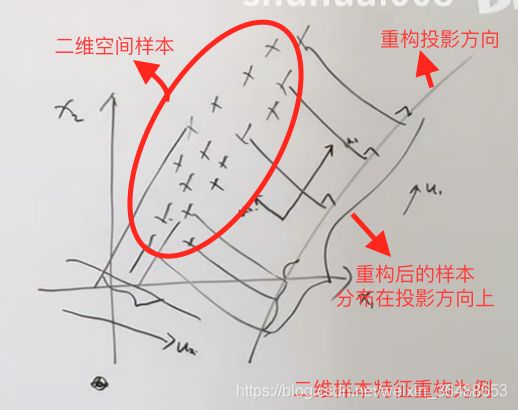
中心化：$x_i-\overline{X}$
投影方向为：$u_1$
根据如图所示的投影定理，则有：

$J=({\sum }_{i=1}^N(x_i-\overline{X}{)}^T{u}_1{)}^2$
$=J={\sum }_{i=1}^N{u_1}^T(x_i-\overline{X})(x_i-\overline{X}{)}^T{u}_1$
$={u_1}^T({\sum }_{i=1}^N\frac{1}{N}(x_i-\overline{X})(x_i-\overline{X}{)}^T)u_1$
$={u_1}^{T}S{u}_1$

则PCA的求解可以看作带约束的优化问题：
$$\{\begin{array}{l}{u}_1^{\prime }=argmax{u}_1^{T}S{u}_1\\ s.t.u_1^T{u}_1=1\end{array}$$
根据拉格朗日乘子法：
$$f(u,\lambda )=u_1^{T}S{u}_1+\lambda (u_1^T{u}_1-1)$$
求偏导：
$$\frac{\partial f}{\partial u_1}=2S{u}_1-\lambda 2u_1=0$$
则有：
$$S{u}_1=\lambda u_1$$

可以看出PCA其实是对特征空间的重构。每选定一个方向，就存在一个对应的特征值。新的重构坐标体系为$u_1,u_2,...,u_p$，则每个中心化后的的重构样本可以表示为：
$$x_i=\sum _{k=1}^p(x_i^T{u}_k)u_k$$
而降维就是针对重构的特征空间样本根据需要保留空间维度，从所有的$p$个空间中选择$q$个维度作为保留，则降维后的样本表示为：
$$x_i^{\prime }=\sum _{k=1}^q(x_i^T{u}_k)u_k$$
则最小重构代价可以表示为：
$$J=\frac{1}{N}\sum _{i=1}^N||x_i-x_i^{\prime }|{|}^2=\frac{1}{N}\sum _{k=q+1}^p||x_i-x_i^{\prime }|{|}^2$$
$$=\frac{1}{N}\sum _{i=1}^N\sum _{k=q+1}^p(x_i^T{u}_k{)}^2$$
考虑中心化：
$$=\frac{1}{N}\sum _{i=1}^N\sum _{k=q+1}^p((x_i-\overline{X}{)}^T{u}_k{)}^2$$
$$=\sum _{k=q+1}^p\sum _{i=1}^N\frac{1}{N}((x_i-\overline{X}{)}^T{u}_k{)}^2=\sum _{k=q+1}^p{u}_k^{T}S{u}_k$$
所以从两个角度看PCA会得到相同的结果。

2. PCA实操

sklearn中降维算法都包含在decomposition模块中。

2.1 重要参数n_components

代表降维后需要的维度，即降维后需要保留的特征数量。

2.1.1 高维数据的可视化特征分布

若要对数据进行可视化，则需要将特征降维到二维（三维也可）。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
iris = load_iris()
y = iris.target
X = iris.data
import pandas as pd
print(pd.DataFrame(X))

pca = PCA(n_components=2)
pca = pca.fit(X) # 拟合模型
X_dr = pca.transform(X) # 获取新矩阵
# 一步到位：X_dr = PCA(2).fit_transform(X)

# 取出分类为0的样本数据的第一个特征
X_dr[y == 0, 0]
# 取出分类为0的样本数据的第二个特征
X_dr[y == 0, 2]

# 画图，也可以循环画
plt.figure()
plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0])
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
plt.legend()
plt.title("PCA of IRIS dataset")
plt.show()

# 查看新特征的可解释性方差大小
print(pca.explained_variance_)
# 查看新特征的可解释性方差贡献率(每个新特征携带原占始信息量比例)
print(pca.explained_variance_ratio_)
# 查看降维后信息占原始信息比例总和
print(pca.explained_variance_ratio_.sum())

import numpy as np
# 对列表进行累加
np.consum(pca.explained_variance_ratio_)

2.1.2 其他方式选取n_components

# 可以使用最大似然估计来取n_components的值
pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)

# 按照信息量占比选取n_components
pca_f = PCA(n_componets=0.97, svd_solver="full")
pca_f = pca_f.fit(X)
X_f = pca_f.transform(X)

2.2 参数svd_solver&random_state

也可以从奇异值分解角度来看PCA：

svd_solver有四种：auto（数据量小用full，大的话用randomized）、full（完整地分解出奇异值矩阵）、arpack（可以加速运算，适合特征矩阵较大且为稀疏矩阵）、randomized（适合特征矩阵巨大，计算量庞大）。

2.3 重要属性components_

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
faces = fetch_lfw_people(min_faces_per_people=60)
X = faces.data

# 现实绘制数据集中的图像
# 4行5列 4*5=20张图
# figsize是画布大小
fig, axes = plt.subplot(4, 5, figsize=(8, 4), subplot_kw={"xticks":[], "yticks":[]})# 不显示坐标轴
for i, ax in enumerate(axes.flat):
	ax.imshow(faces.images[i,:,:], cmap="gray")

pca = PCA(150).fit(X)
V = pca.components_
# 可视化components_核心信息
fig, axes = plt.subplot(3, 8, figsize=(8, 4), subplot_kw={"xticks":[], "yticks":[]})# 不显示坐标轴
for i, ax in enumerate(axes.flat):
	ax.imshow(V[i,:].reshape(62,47), cmap="gray")

2.4 重要接口inverse_transform

降维是不可逆的，即使采用该接口也无法恢复。

X_inverse = pca.inverse_transform(X_dr)
fig, axes = plt.subplot(2, 10, figsize=(10, 2.5), subplot_kw={"xticks":[], "yticks":[]})# 不显示坐标轴
for i in range(10):
	ax[0,i].imshow(faces.images[i,:,:], cmap="binary_r")
	ax[1,i].imshow(X_inverse[i].reshape(62,47), cmap="binary_r")

2.5 用PCA做噪音过滤

from sklearn.datasets import load_digits

digits = load_digits()
# 查看标签
print(set(digits.target.tolist()))
# 绘图
def plot(data):
	fig, axes = plt.subplot(4, 10, figsize=(10, 4), subplot_kw={"xticks":[], "yticks":[]})# 不显示坐标轴
	for i, ax in enumerate(axes.flat):
		ax.imshow(data[i].reshape(8,8), cmap="binary")

# 为数据加上噪音
np.random.RandomState(42)
noisy = np.random.normal(digits.data, 2)
plot(noisy)

pca = PCA(0.5, svd_solver="full").fit(noisy)
X_dr = pca.transform(noisy)

witout_noise = pca.inverse_transform(X_dr)
plot(without_noise)

2.6 实战：手写数据集降维

已经导过的包就不导了。

from sklearn.esemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
data = pd.read_csv("数据集CSV路径")
X = data.iloc[:, 1:]
y = data.iloc[:,0]

# 画累计方差贡献率曲线，找最佳降维后维度的范围
pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.consum(pca.line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance")
plt.show()

# 降维后的学习曲线，继续缩小最佳维度的范围
score = []
# 缩小范围（10，25）再次绘制学习曲线
for i in range(1, 101, 10):
	X_dr = PCA(i).fit_transform(X)
	once = cross_val_score(RFC(n_estimator=10, random_state=0), X_dr, y, cv=5).mean()
	score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1, 101, 10), score)
plt.show()

# 找到最佳的参数后确定将维维度
X_dr = PCA(23).fit_transform(X)
cross_val_score(RFC(n_estimator=100, random_state=0), X_dr, y, cv=5).mean()

# 使用KNN来训练
from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(), X_dr, y, cv=5).mean()

# KNN的k值学习曲线
score = []
# 确定k值为3
for i in range(10):
	X_dr = PCA(23).fit_transform(X)
	once = cross_val_score(KNN(i+1), X_dr, y, cv=5).mean()
	score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10), score)
plt.show()