动态规划----解决“打家劫舍”问题
CSDN话题挑战赛第2期
参赛话题:面试宝典
- 序:下面题解代码仅用了Java和c++两种语言进行了编写,算法你懂得了那个思想,哪种语言编写都一样。
198.打家劫舍
题目:
浏览完题目(抓关键字):
房屋内的金额是非负整数;小偷不能同时偷取俩相邻的房间;最高金额(题目输出,也是题目所求);再看输入是一个各个房间所存在的金额序列,加上输出是最高金额。有序列,要求最...我们可以考虑用动态规划解题。
想到动态规划解决这题后,就开始动态规划三步走了:
1. 定义dp数组含义:
dp[i]元素值表示从头号房开始偷到 i 号房可以偷到的最大金额
2. 根据题目给出的属性写出递推公式(也就是根据题目所给的属性和dp数组i前的元素推出dp[i] ):
我们需要考虑的无疑就两种情况,偷 i 号房里的钱,不偷 i 房里的钱。
(记得dp数组的自己定义的含义)
情况1:偷 i 房里的钱,那 dp[i] = dp[i-2] + nums[i]
情况2:不偷 i 房里的钱,那 dp[i] = dp[i-1] (不偷的话可以偷到的最大金额当然是dp[i-1])
递推公式就是把这俩情况总结成一公式:
dp[i] = max(dp[i-1],dp[i-2] + nums[i])
3. 对dp数组进行初始化
这题我们需要初始化dp[0] 与 dp[1](所以输入的序列长度应该大于或等于2,记得序列为1或2时自身去返回其最大值)。
由于索引0前没元素了:dp[0] = nums[0]
由于索引不可以为负数:dp[1] = max(nums[1],dp[0])
而后就可以写解决该题的代码了。
C++版:
class Solution {
public:
int rob(vector& nums) {
if(nums.size()==1)
return nums[0];
else if(nums.size()==2)
return max(nums[0],nums[1]);
vector dp(nums.size(),0);//该容器内元素表示从头号房开始偷到这偷到的最大金额
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i=2;i Java版:
class Solution {
public int rob(int[] nums) {
if(nums.length==1)
return nums[0];
else if(nums.length==2)
return Math.max(nums[0],nums[1]);
int[] dp = new int[nums.length];//该容器内元素表示从头号房开始偷到i偷到的最大金额
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
for(int i=2;i213.打家劫舍 ||
题目:
浏览题目:这题相比第一题房子排布变成了一个圈,也就是第一个房间和最后一个房间是相邻的,其余关系属性啥的没变。
既然和第一题有关,那我们可以想办法转化成第一题那样可以用动态规划解决的题型。
怎么转化呢?可以通过切开首尾这样俩者就不会相邻了,就可以转化成上一题的逻辑解题了。
三种切法:
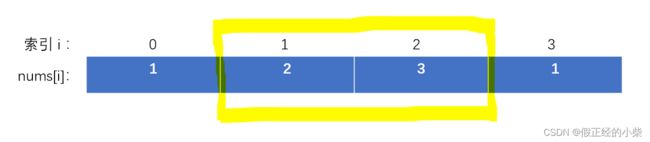
第一种(把首尾房间都去除):
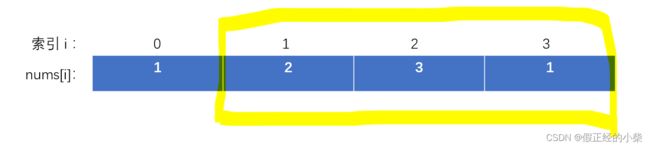
第二种(把首房间去除):
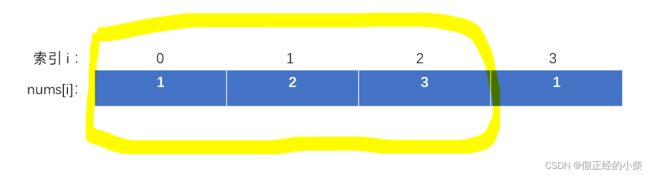
第三种(把尾房间去除):
由图可以看出第二种和第三种是包含了第一种的情况的,所以不用考虑,该题就转化俩种情况,以第一题的逻辑解法就可以了。
代码如下:
C++版:
class Solution {
private:
//打家劫舍求所偷最大金额
int uprob(vector nums){
if(nums.size()==1)
return nums[0];
vector dp(nums.size(),0);
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i=2;i& nums) {
if(nums.size()==1)
return nums[0];
int situation2 = uprob(vector(nums.begin()+1,nums.end()));//考虑情况二
int situation3 = uprob(vector(nums.begin(),nums.end()-1));//考虑情况三
return max(situation2,situation3);//两种情况的最大的就是偷的最大金额了
}
}; Java版:
class Solution {
public int rob(int[] nums) {
if(nums.length==1)
return nums[0];
//情况2
int[] dp2 = new int[nums.length-1];
//长度为1的话只能偷最后一个房间
if(dp2.length==1)
dp2[dp2.length-1] = nums[1];
else{
dp2[0] = nums[1];
dp2[1] = Math.max(nums[2],nums[1]);
for(int i=3;i337.打家劫舍 |||
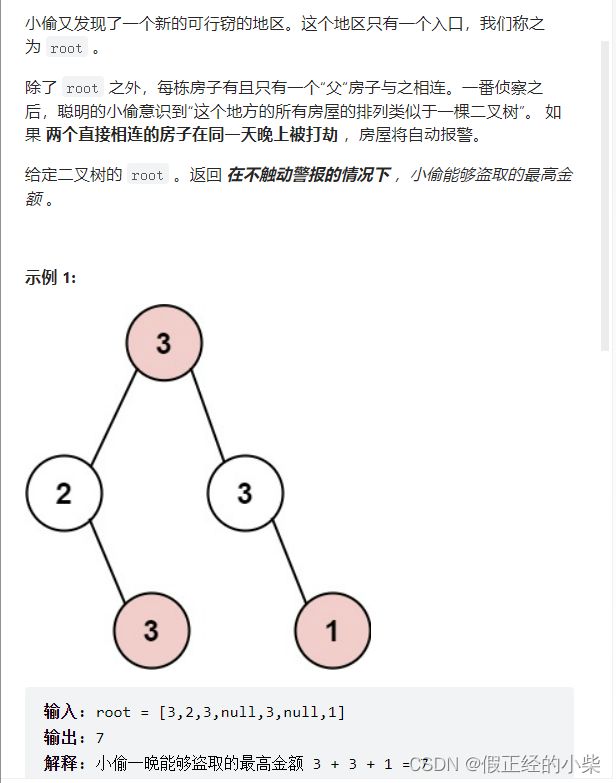
题目:
(虽然这个小区排布像二叉树似的,但并不影响小偷去偷money)
这题仍然可以用题一的解题思路去解。
还是两种情况,要么就抢这个结点,要么就步抢。抢这个结点的话,就不考虑抢左右孩子的结点;不抢该结点的话,就考虑抢左右孩子的结点。抢与不抢看哪种可以偷到更多的钱。
代码如下:
C++版:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
//记录访问过了的结点
unordered_map mp;
public:
int rob(TreeNode* root) {
if(!root)
return 0;
//没有子孩子只能偷该结点
if(!root->left&&!root->right)
return root->val;
//如果这个结点刚问过了那就直接返回就行了
if(mp[root])
return mp[root];
//抢该结点
int val1 = root->val;
if(root->left) val1 += rob(root->left->left) + rob(root->left->right);
if(root->right) val1 += rob(root->right->left) + rob(root->right->right);
//不抢该结点
int val2 = rob(root->left) + rob(root->right);
mp[root] = max(val1,val2);
return mp[root];
}
}; 今日励志: