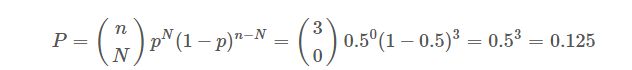numpy.where与numpy.random.multinomial用法

umpy.where() 有两种用法：

1. np.where(condition, x, y) 满足条件(condition)，输出x，不满足输出y
2. np.where(condition) 只有条件 (condition)，没有x和y，则输出满足条件 (即非0) 元素的坐标 (等价于numpy.nonzero)。这里的坐标以tuple的形式给出，通常原数组有多少维，输出的tuple中就包含几个数组，分别对应符合条件元素的各维坐标。

1. np.where(condition, x, y)

满足条件(condition)，输出x，不满足输出y。

import numpy as np
aa = np.arange(10)
Out[4]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.where(aa,1,-1)
Out[5]: array([-1,  1,  1,  1,  1,  1,  1,  1,  1,  1])   # 0为False，所以第一个输出-1

2. np.where(condition)

只有条件 (condition)，没有x和y，则输出满足条件 (即非0) 元素的坐标 (等价于numpy.nonzero)。这里的坐标以tuple的形式给出，通常原数组有多少维，输出的tuple中就包含几个数组，分别对应符合条件元素的各维坐标。

np.where(aa > 5)
Out[6]: (array([6, 7, 8, 9], dtype=int64),)
aa[np.where(aa > 5)] 
Out[7]: array([6, 7, 8, 9])

numpy.random.multinomial函数

这是 numpy 提供的随机二项式分布实现，二项式分布(binomial distribution)如下表示:

函数原型如下：

numpy.random.RandomState.binomial(n, p, size=None)

表示对一个二项分布进行采样，size表示采样的次数，参数中的n, p分别对应于公式中的n,pn,p，函数的返回值表示n中成功（success）的次数（也即NN）。 举个例子，比如掷骰子，一共3个硬币，每个都投一次，三个都是正面朝上的概率是多少？

这个使用简单的概率统计知识很容易计算得到：

 

 使用上述函数计算大概值则是做足够多次的试验，统计其中全为正面朝上的概率，通过频率计算概率，如下：

---

参考：

• https://www.cnblogs.com/massquantity/p/8908859.html
• https://suool.net/2018/12/14/Numpy-Where/