【GAT】如何理解Graph Attention Network（注意力机制）？

论文链接：Graph Attention Networks
Github链接：https://github.com/PetarV-/GAT

1 GAT的背景

2 GAT的主要结构

3 GAT的创新点是什么？

先介绍GCN的局限性，然后介绍GAT的创新点。

GAT的局限性

• GCN 无法完成inductive任务（unseen node in test）

• GCN 无法分配不同的学习权重给不同的neighbor

• 对于一个图结构训练好的模型，不能运用于另一个图结构（所以此文称自己为半监督的方法）

GAT的创新点

• 引入masked self-attentional layers 来改进 GCN 无法分配不同的学习权重给不同的neighbor的缺点
• 对不同的相邻节点分配相应的权重，既不需要矩阵运算，也不需要事先知道图结构
• 四个数据集上达到state-of-the-art的准确率Cora、Citeseer、Pubmed、protein interaction

4 masked self-attentional layers

4.1 Attention Mechanism

神经网络中的注意力机制（Attention Mechanism）是在计算能力有限的情况下，将计算资源分配给更重要的任务，同时解决信息超载问题的一种资源分配方案。这就类似于人类的视觉注意力机制，通过扫描全局图像，获取需要重点关注的目标区域，而后对这一区域投入更多的注意力资源，获取更多与目标有关的细节信息，而忽视其他无关信息。

有关注意力机制的详细内容请参考：https://www.cnblogs.com/Luv-GEM/p/10712256.html、https://blog.csdn.net/hahajinbu/article/details/81940355

4.2 Self-attention Models

在一般任务的Encoder-Decoder框架中，输入Source和输出Target内容是不一样的，比如对于英-中机器翻译来说，Source是英文句子，Target是对应的翻译出的中文句子，Attention机制发生在Target的元素Query和Source中的所有元素之间。

而Self Attention顾名思义，指的不是Target和Source之间的Attention机制，而是Source内部元素之间或者Target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力计算机制。Self Attention可以捕获同一个句子中单词之间的一些句法特征 或者 语义特征。

有关自注意力模型的详细内容请参考：https://zhuanlan.zhihu.com/p/37601161

4.3 Masked的含义？

相当于盖住你当前关注的词的后面所有词，我只关心前面出现的词，而后面的词我不关注，因为我要生成后面的词。

有关Masked自注意力机制的详细内容请参考：https://zhuanlan.zhihu.com/p/94998435

4.4 multi-head attention机制

神似卷积神经网络里的多通道，GAT 引入了多头注意力来丰富模型的能力和稳定训练的过程。每一个注意力的头都有它自己的参数。如何整合多个注意力机制的输出结果一般有两种方式：

• 拼接
  $$h_i^{(l+1)}={\Vert }_{k=1,\dots ,K}\sigma \left(\sum _{j\in N(i)}{\alpha }_{ij}^k{W}^k{h}_j^{(l)}\right)\text{\hspace{1em}(5)}$$
• 平均
  $$h_i^{(l+1)}=\sigma \left(\frac{1}{k}\sum _{k=1}^K\sum _{j\in N(i)}{\alpha }_{ij}^k{W}^k{h}_j^{(l)}\right)\text{\hspace{1em}(6)}$$

4.5 Transformer Vs GAT

NLP中大火的Transformer和GAT本质在做一样的事情。Transformer利用self-attention机制将输入中的每个单词用其上下文的加权来表示，而GAT是利用self-attention机制将每个节点用其邻居的加权来表示。下面是经典的Transformer公式，

$$Attention(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$$

这里的 $Q,K,V$ 是一个单词的三种描述， 其中，$Q$ 是当单词作为上下文的中心位置时的表示，$K$ 是当单词作为上下文时的表示， $V$ 是当单词作为加权输入时的表示。

因此， $Q{K}^T$ 其实代表了单词之间的相似性，在经过softmax归一化之后就可以得到注意力权重。有了注意力权重，我们再对上下文单词的表示进行加权，就可以得到单词的表示了。

上述过程和GAT的核心思想非常相似：都是通过探索输入之间的关联性(注意力权重)，通过对上下文信息(句子上下文/节点邻居)进行聚合，来获得各个输入(单词/节点)的表示。

Transformer和GAT的主要区别是:

• 在GAT中，作者对自注意力进行了简化。每个节点无论是作为中心节点/上下文/聚合输出，都只用一种表示 $h$。也就是说，在GAT中，$Q=K=V$。
• 在图上，节点的邻居是一个集合，具有不变性。Transformer将文本隐式的建图过程中丢失了单词之间的位置关系，这对NLP的一些任务是很致命的。为了补偿这种建图损失的位置关系，Transformer用了额外了的位置编码来描述位置信息。

5 深入了解GAT

5.1 GAT的输入如何获得？

GAT的输入是节点的特征向量，可以通过随机初始化来得到初始节点向量。

5.2 GAT适合处理有向图？

GAT摒弃了拉普拉斯矩阵，进行逐点计算（node-wise）。
GCN使用拉普拉斯矩阵，并进行是逐层运算。

个人理解：只要在公式中没有使用拉普拉斯矩阵特征分解的方法都可以说适用于有向图，比如GraphSage和GAT，因此特征分解的充要条件只有对称矩阵才能满足，而有向图的拉普拉斯矩阵并不是对称矩阵。

5.3 inductive和transductive ？

GCN 本质是频域卷积，是一种全图的计算方式，一次卷积更新所有节点特征，计算过程涉及表征图结构的拉普拉斯矩阵，所以一旦出现了没有见过的图结构，拉普拉斯矩阵随之变化，以前训练好的基于原图结构的模型也就失效了——transductive（顶点的特征变了）

GAT 逐顶点运算方式，学习参数是 $W$ 与 $a(\cdot )$ 仅与顶点特征相关，与图的结构（邻接矩阵$A$）毫无关系，所以可计算新图——inductive

训练的参数只有 $a(\cdot )$ 和 $W$，无论节点个数如何变化，邻居节点间这两个参数是共享的，所以逐节点训练是可行的。

此处参考知乎：https://www.zhihu.com/question/409415383、https://zhuanlan.zhihu.com/p/74242097

5.4 共享参数W

GAT 共享参数 $W$ 的线性映射对顶点特征增维，这个特征增维是数据维度的变换。

GCN中的矩阵乘法里的矩阵系数是待训练的卷积核参数 $\Theta$ 和拉普拉斯矩阵 $L$ 的共同表达，而 $L$ 矩阵是一个表征图整体结构的矩阵，所以说它是一步卷积。

GCN逐层更新公式：输入节点矩阵$X\in {\mathbb{R}}^{N\times C}$, 每个输入节点有$C$个通道(channels, 即每个图节点有$C$维特征)，卷积操作包含$F$个滤波器(filters)或特征映射(feature maps), 如下：
$$Y=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X\Theta \right)$$
其中$\Theta \in {\mathbb{R}}^{C\times F}$ 是filters的参数矩阵, $Y\in {\mathbb{R}}^{N\times F}$ 是卷积之后的节点矩阵。

而GAT中 $L$ 不固定，是由注意力系数矩阵 $A=(a_{ij}^k{)}_{n\times n}$ 组成，而 $A$ 是逐点计算和整图结构关系不大，所以GAT训练的 $W$ 可以在test时继续用。

W的维度并不受图的具体拓扑结构限制，只和你设置的hidden layer维度有关。

5.5 GAT核心公式

图注意力模型GAT用注意力机制替代了图卷积中固定的标准化操作。下图和公式定义了如何对第 $l$ 层节点特征做更新得到第 $l+1$ 层节点特征：

$$z_i^{(l)}={\mathbf{W}}^{(l)}{h}_i^{(l)}\text{\hspace{1em}(1)}$$

$$e_{ij}^{(l)}=\mathrm{LeakyReLU}\left(a^{(l{)}^T}\left(z_i^{(l)}\Vert z_j^{(l)}\right)\right)\text{\hspace{1em}(2)}$$

$${\alpha }_{ij}^{(l)}=\frac{\exp \left(e_{ij}^{(l)}\right)}{{\sum }_{k\in \mathcal{N}(i)}\exp \left(e_{ik}^{(l)}\right)}\text{\hspace{1em}(3)}$$

$$h_i^{(l+1)}=\sigma \left(\sum _{j\in \mathcal{N}(i)}{\alpha }_{ij}^{(l)}{z}_j^{(l)}\right)\text{\hspace{1em}(4)}$$

对于上述公式的一些解释：

• 公式 (1) 对 $l$ 层节点的embedding $h_i^{(l)}$ 做了一个线性变换, ${\mathbf{W}}^{(l)}$ 是一个该变换的一个可训练的参数。
• 公式 (2) 计算了成对节点间的原始注意力分数。它首先拼接了两个节点的embedding $z$, 注意||在这里表示拼接; 随后对拼接好的embedding以及一个可学习的权重向量 $a^{(l)}$ 做点积; 最后应用了一个LeakyReLU 激活函数。这一形式的注意力机制通常被称为加性注意力（additive attention），区别于Transformer(Attention Is All You Need) 里的点积注意力（dot-product attention）。
• 公式 (3) 对于一个节点所有入边得到的原始注意力分数应用了一个softmax操作, 得到了注意力权重。
• 公式 (4)， 形似GCN的节点特征更新规则，对所有邻节点的特征做了基于注意力的加权求和。

核心公式详细内容请参考：https://docs.dgl.ai/tutorials/models/1_gnn/9_gat.html

6 图注意力机制的类型

目前主要有三种注意力机制算法，它们分别是：学习注意力权重(Learn attention weights)，基于相似性的注意力(Similarity-based attention)，注意力引导的随机游走(Attention-guided walk)。这三种注意力机制都可以用来生成邻居的相对重要性，下文会阐述他们之间的差异。

首先我们对“图注意力机制”做一个数学上的定义：

定义（图注意力机制）：给定一个图中节点$v_0$ 和$v_0$的邻居节点 $\left\{v_1,\cdots ,v_{|{\Gamma }_{v_0}|}\right\}\in {\Gamma }_{v_0}$ (这里的 ${\Gamma }_{v_0}$ 和GraphSAGE博文中的 $\mathcal{N}(v_0)$ 表示一个意思)。注意力机制被定义为将${\Gamma }_{v_0}$中每个节点映射到相关性得分(relevance score)的函数$f^{\prime }:\left\{v_0\right\}\times {\Gamma }_{v_0}\to [0,1]$，相关性得分表示该邻居节点的相对重要性。满足：

$$\sum _{i=1}^{|{\Gamma }_{v_0}|}{f}^{\prime }\left(v_0,v_i\right)=1$$

下面再来看看这三种不同的图注意力机制的具体细节

6.1 学习注意力权重

学习注意力权重的方法来自于Velickovic et al. 2018 其核心思想是利用参数矩阵学习节点和邻居之间的相对重要性。

给定节点$v_0,v_1,\cdots ,v_{|{\Gamma }_{x_0}|}$相应的特征(embedding) $${\mathbf{x}}_0,{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_{|{\Gamma }_{o^{\ast }}|}$$ ，节点$v_0$和节点$v_j$注意力权重${\alpha }_{0,j}$可以通过以下公式计算：

$${\alpha }_{0,j}=\frac{e_{0,j}}{{\sum }_{k\in {\Gamma }_{v_0}}{e}_{0,k}}$$

其中，$e_{0,j}$ 表示节点$v_j$对节点$v_0$的相对重要性。在实践中，可以利用节点的属性结合softmax函数来计算$e_{0,j}$间的相关性。比如，GAT 中是这样计算的：

$${\alpha }_{0,j}=\frac{\exp \left(\text{ LeakyReLU }\left(\mathbf{a}\left[{\mathbf{W}\mathbf{x}}_0\Vert {\mathbf{W}\mathbf{x}}_j\right]\right)\right)}{{\sum }_{k\in {\Gamma }_{v_0}}\exp \left(\text{ LeakyReLU }\left(\mathbf{a}\left[\mathbf{W}{\mathbf{x}}_0\Vert \mathbf{W}{\mathbf{x}}_k\right]\right)\right)}$$

其中，$\mathbf{a}$ 表示一个可训练的参数向量, 用来学习节点和邻居之间的相对重要性，$\mathbf{W}$ 也是一个可训练的参数矩阵，用来对输入特征做线性变换，$||$表示向量拼接(concate)。

如上图，对于一个目标对象$v_0$，$a_{0,i}$ 表示它和邻居$v_i$的相对重要性权重。$a_{0,i}$可以根据 $v_0$ 和 $v_i$ 的 embedding $x_0$ 和 $x_i$ 计算，比如图中${\alpha }_{0,4}$ 是由 $x_0,x_4,\mathbf{W},\mathbf{a}$ 共同计算得到的。

6.2 基于相似性的注意力

上面这种方法使用一个参数向量$\mathbf{a}$学习节点和邻居的相对重要性，其实另一个容易想到的点是：既然我们有节点$v$的特征表示$x$，假设和节点自身相像的邻居节点更加重要，那么可以通过直接计算$x$之间相似性的方法得到节点的相对重要性。这种方法称为基于相似性的注意力机制，比如说论文 TheKumparampil et al. 2018 是这样计算的：

$${\alpha }_{0,j}=\frac{\exp \left(\beta \cdot \cos \left(\mathbf{W}{\mathbf{x}}_0,\mathbf{W}{\mathbf{x}}_j\right)\right)}{{\sum }_{k\in {\Gamma }_{v_0}}\exp \left(\beta \cdot \cos \left(\mathbf{W}{\mathbf{x}}_0,\mathbf{W}{\mathbf{x}}_k\right)\right)}$$

其中，$\beta$ 表示可训练偏差(bias)，$\cos$函数用来计算余弦相似度，和上一个方法类似，$\mathbf{W}$ 是一个可训练的参数矩阵，用来对输入特征做线性变换。

这个方法和上一个方法的区别在于，这个方法显示地使用$\cos$函数计算节点之间的相似性作为相对重要性权重，而上一个方法使用可学习的参数$\mathbf{a}$学习节点之间的相对重要性。

6.3 注意力引导的游走法

前两种注意力方法主要关注于选择相关的邻居信息，并将这些信息聚合到节点的embedding中。第三种注意力的方法的目的不同，我们以Lee et al. 2018 作为例子：

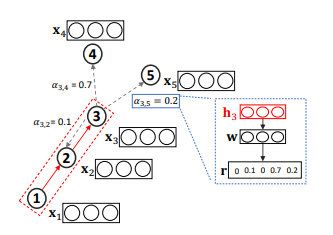
GAM方法在输入图进行一系列的随机游走，并且通过RNN对已访问节点进行编码，构建子图embedding。时间$t$的RNN隐藏状态 $${\mathbf{h}}_t\in {\mathbb{R}}^h$$ 编码了随机游走中 $1,\cdots ,t$ 步访问到的节点。然后，注意力机制被定义为函数 $f^{\prime }:{\mathbb{R}}^h\to {\mathbb{R}}^k$，用于将输入的隐向量$$f^{\prime }\left({\mathbf{h}}_t\right)={\mathbf{r}}_{t+1}$$映射到一个$k$维向量中，可以通过比较这$k$维向量每一维的数值确定下一步需要优先游走到哪种类型的节点(假设一共有$k$种节点类型)。下图做了形象的阐述：

如上图，$h_3$聚合了长度$L=3$的随机游走得到的信息$\left(x_1,x_2,x_3\right)$，我们将该信息输入到排序函数中，以确定各个邻居节点的重要性并用于影响下一步游走。

7 后话

至此，图注意力机制就讲完了，还有一些细节没有涉及，比如在 GAT论文 中讨论了对一个节点使用多个注意力机制(multi-head attention), 在AGNN论文中分析了注意力机制是否真的有效，详细的可以参考原论文。

8 Reference

Attention Models in Graphs: A Survey

Graph Attention Networks

Attention-based Graph Neural Network for Semi-supervised Learning

Graph Classification using Structural Attention