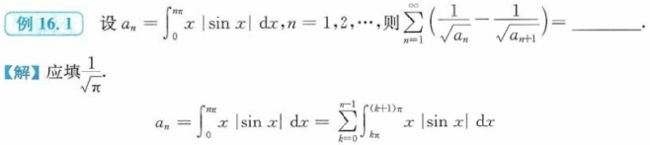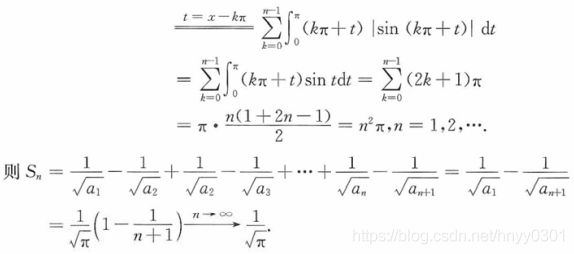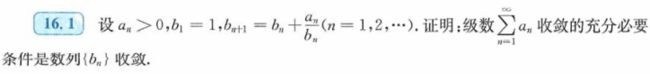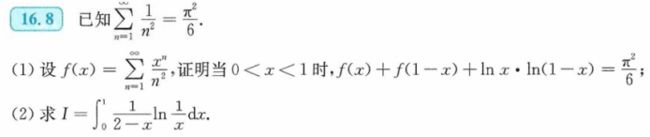高等数学张宇18讲 第十三讲 无穷级数
目录
- 例题十三
-
- 例13.9 设 f ( x ) f(x) f(x)在点 x = 0 x=0 x=0处存在二阶导数 f ′ ′ ( 0 ) f''(0) f′′(0),且 lim x → 0 f ( x ) x = 0 \lim\limits_{x\to0}\cfrac{f(x)}{x}=0 x→0limxf(x)=0。试证明级数 ∑ n = k ∞ ∣ f ( 1 n ) ∣ \sum\limits_{n=k}^\infty\left|f\left(\cfrac{1}{n}\right)\right| n=k∑∞∣∣∣∣∣f(n1)∣∣∣∣∣收敛,其中 k k k为足够大的正整数。
- 例13.12 已知级数 ∑ n = 1 ∞ u n \displaystyle\sum\limits_{n=1}^\infty u_n n=1∑∞un绝对收敛,判断 ∑ n = 1 ∞ u n 2 1 + u n 2 \displaystyle\sum\limits_{n=1}^\infty\cfrac{u_n^2}{1+u_n^2} n=1∑∞1+un2un2的敛散性,其中 u n ≠ 0 u_n\ne0 un=0。
- 例13.30 设 a 0 = 3 , 3 n a n + 3 ( n − 1 ) a n − 1 = 2 a n − 1 a_0=3,3na_n+3(n-1)a_{n-1}=2a_{n-1} a0=3,3nan+3(n−1)an−1=2an−1,证明当 ∣ x ∣ < 1 |x|<1 ∣x∣<1时, ∑ n = 1 ∞ a n x n \displaystyle\sum\limits_{n=1}^\infty a_nx^n n=1∑∞anxn收敛,并求其和函数。
- 习题十三
-
- 13.5 讨论级数 ∑ n = 3 ∞ ( − 1 ) n ( n 2 − 3 n + 2 ) x \displaystyle\sum\limits_{n=3}^\infty\cfrac{(-1)^n}{(n^2-3n+2)^x} n=3∑∞(n2−3n+2)x(−1)n的敛散性, x x x为实数。
- 新版例题十六
-
- 例16.1
- 例16.3
- 例16.8(4)
- 例16.13
- 例16.16
- 例16.21
- 例16.24
- 例16.30
- 例16.40
- 新版习题十六
-
- 16.1
- 16.8
- 写在最后
例题十三
例13.9 设 f ( x ) f(x) f(x)在点 x = 0 x=0 x=0处存在二阶导数 f ′ ′ ( 0 ) f''(0) f′′(0),且 lim x → 0 f ( x ) x = 0 \lim\limits_{x\to0}\cfrac{f(x)}{x}=0 x→0limxf(x)=0。试证明级数 ∑ n = k ∞ ∣ f ( 1 n ) ∣ \sum\limits_{n=k}^\infty\left|f\left(\cfrac{1}{n}\right)\right| n=k∑∞∣∣∣∣∣f(n1)∣∣∣∣∣收敛,其中 k k k为足够大的正整数。
解 由 lim x → 0 f ( x ) x = 0 \lim\limits_{x\to0}\cfrac{f(x)}{x}=0 x→0limxf(x)=0及 f ( x ) f(x) f(x)在点 x = 0 x=0 x=0处连续可知 f ( 0 ) = 0 f(0)=0 f(0)=0,且 f ′ ( 0 ) = lim x → 0 f ( x ) − f ( 0 ) x − 0 = lim x → 0 f ( x ) x = 0 f'(0)=\lim\limits_{x\to0}\cfrac{f(x)-f(0)}{x-0}=\lim\limits_{x\to0}\cfrac{f(x)}{x}=0 f′(0)=x→0limx−0f(x)−f(0)=x→0limxf(x)=0,于是
lim x → 0 f ( x ) x 2 = 洛必达法则 lim x → 0 f ′ ( x ) 2 x = lim x → 0 f ′ ( x ) − f ′ ( 0 ) 2 ( x − 0 ) = 1 2 f ′ ′ ( 0 ) . \lim\limits_{x\to0}\cfrac{f(x)}{x^2}\xlongequal{\text{洛必达法则}}\lim\limits_{x\to0}\cfrac{f'(x)}{2x}=\lim\limits_{x\to0}\cfrac{f'(x)-f'(0)}{2(x-0)}=\cfrac{1}{2}f''(0). x→0limx2f(x)洛必达法则x→0lim2xf′(x)=x→0lim2(x−0)f′(x)−f′(0)=21f′′(0).
所以 lim n → ∞ ∣ f ( 1 n ) ∣ 1 n 2 = 1 2 ∣ f ′ ′ ( 0 ) ∣ \lim\limits_{n\to\infty}\cfrac{\left|f\left(\cfrac{1}{n}\right)\right|}{\cfrac{1}{n^2}}=\cfrac{1}{2}|f''(0)| n→∞limn21∣∣∣∣∣f(n1)∣∣∣∣∣=21∣f′′(0)∣。用比较判别法的极限形式,级数 ∑ n = k ∞ 1 n 2 \sum\limits_{n=k}^\infty\cfrac{1}{n^2} n=k∑∞n21收敛,故 ∑ n = k ∞ ∣ f ( 1 n ) ∣ \sum\limits_{n=k}^\infty\left|f\left(\cfrac{1}{n}\right)\right| n=k∑∞∣∣∣∣∣f(n1)∣∣∣∣∣收敛。(这道题主要利用了比较判别法求解)
例13.12 已知级数 ∑ n = 1 ∞ u n \displaystyle\sum\limits_{n=1}^\infty u_n n=1∑∞un绝对收敛,判断 ∑ n = 1 ∞ u n 2 1 + u n 2 \displaystyle\sum\limits_{n=1}^\infty\cfrac{u_n^2}{1+u_n^2} n=1∑∞1+un2un2的敛散性,其中 u n ≠ 0 u_n\ne0 un=0。
解 由不等式 a 2 + b 2 ⩾ 2 a b a^2+b^2\geqslant2ab a2+b2⩾2ab,可知 1 + u n 2 ⩾ 2 ∣ u n ∣ 1+u_n^2\geqslant2|u_n| 1+un2⩾2∣un∣,于是 u n 2 1 + u n 2 ⩽ u n 2 2 ∣ u n ∣ = ∣ u n ∣ 2 \cfrac{u_n^2}{1+u_n^2}\leqslant\cfrac{u_n^2}{2|u_n|}=\cfrac{|u_n|}{2} 1+un2un2⩽2∣un∣un2=2∣un∣,由题设知 ∑ n = 1 ∞ ∣ u n ∣ 2 \displaystyle\sum\limits_{n=1}^\infty\cfrac{|u_n|}{2} n=1∑∞2∣un∣收敛,又 ∑ n = 1 ∞ u n 2 1 + u n 2 \displaystyle\sum\limits_{n=1}^\infty\cfrac{u_n^2}{1+u_n^2} n=1∑∞1+un2un2是正项级数,根据正项级数的比较判别法,原级数收敛。(这道题主要利用了不等式变换求解)
例13.30 设 a 0 = 3 , 3 n a n + 3 ( n − 1 ) a n − 1 = 2 a n − 1 a_0=3,3na_n+3(n-1)a_{n-1}=2a_{n-1} a0=3,3nan+3(n−1)an−1=2an−1,证明当 ∣ x ∣ < 1 |x|<1 ∣x∣<1时, ∑ n = 1 ∞ a n x n \displaystyle\sum\limits_{n=1}^\infty a_nx^n n=1∑∞anxn收敛,并求其和函数。
解 由题设递推式,得 n a n = ( 5 3 − n ) a n − 1 na_n=\left(\cfrac{5}{3}-n\right)a_{n-1} nan=(35−n)an−1,按正项级数的比值判别法,记 u n ( x ) = a n x n u_n(x)=a_nx^n un(x)=anxn,有
lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ = lim n → ∞ ∣ u n ( x ) u n − 1 ( x ) ∣ = lim n → ∞ ∣ a n x n a n − 1 x n − 1 ∣ = lim n → ∞ ∣ a n a n − 1 ∣ ∣ x ∣ = lim n → ∞ ∣ 5 3 − n n ∣ ∣ x ∣ = ∣ x ∣ < 1 \lim\limits_{n\to\infty}\left|\cfrac{u_{n+1}(x)}{u_n(x)}\right|=\lim\limits_{n\to\infty}\left|\cfrac{u_{n}(x)}{u_{n-1}(x)}\right|=\lim\limits_{n\to\infty}\left|\cfrac{a_nx^n}{a_{n-1}x^{n-1}}\right|=\lim\limits_{n\to\infty}\left|\cfrac{a_n}{a_{n-1}}\right||x|=\lim\limits_{n\to\infty}\left|\cfrac{\cfrac{5}{3}-n}{n}\right||x|=|x|<1 n→∞lim∣∣∣∣∣un(x)un+1(x)∣∣∣∣∣=n→∞lim∣∣∣∣∣un−1(x)un(x)∣∣∣∣∣=n→∞lim∣∣∣∣∣an−1xn−1anxn∣∣∣∣∣=n→∞lim∣∣∣∣∣an−1an∣∣∣∣∣∣x∣=n→∞lim∣∣∣∣∣∣∣∣n35−n∣∣∣∣∣∣∣∣∣x∣=∣x∣<1
即当 ∣ x ∣ < 1 |x|<1 ∣x∣<1时, ∑ n = 1 ∞ a n x n \displaystyle\sum\limits_{n=1}^\infty a_nx^n n=1∑∞anxn收敛。记 S ( x ) = ∑ n = 1 ∞ a n x n S(x)=\displaystyle\sum\limits_{n=1}^\infty a_nx^n S(x)=n=1∑∞anxn,则
S ( x ) = ∑ n = 1 ∞ a n x n = ∑ n = 1 ∞ 1 n ( 5 3 − n ) a n − 1 x n = ∑ n = 1 ∞ 1 n ( 5 3 a n − 1 − n a n − 1 ) x n = 5 3 ∑ n = 1 ∞ 1 n a n − 1 x n − ∑ n = 1 ∞ a n − 1 x n = 5 3 ∫ 0 x ( ∑ n = 1 ∞ 1 n a n − 1 t n ) ′ d t − x ∑ n = 1 ∞ a n − 1 x n = 5 3 ∫ 0 x ( ∑ n = 1 ∞ a n − 1 t n − 1 ) d t − x ( ∑ n = 1 ∞ a n x n + a 0 ) = 5 3 ∫ 0 x ( ∑ n = 1 ∞ a n t n + a 0 ) d t − x ( ∑ n = 1 ∞ a n x n + a 0 ) = 5 3 ∫ 0 x [ S ( t ) + 3 ] d t − x [ S ( x ) + 3 ] . \begin{aligned} S(x)&=\displaystyle\sum\limits_{n=1}^\infty a_nx^n=\displaystyle\sum\limits_{n=1}^\infty\cfrac{1}{n}\left(\cfrac{5}{3}-n\right)a_{n-1}x^n\\ &=\displaystyle\sum\limits_{n=1}^\infty\cfrac{1}{n}\left(\cfrac{5}{3}a_{n-1}-na_{n-1}\right)x^n=\cfrac{5}{3}\displaystyle\sum\limits_{n=1}^\infty\cfrac{1}{n}a_{n-1}x^n-\displaystyle\sum\limits_{n=1}^\infty a_{n-1}x^n\\ &=\cfrac{5}{3}\displaystyle\int^x_0\left(\displaystyle\sum\limits_{n=1}^\infty\cfrac{1}{n}a_{n-1}t^n\right)'\mathrm{d}t-x\displaystyle\sum\limits_{n=1}^\infty a_{n-1}x^n\\ &=\cfrac{5}{3}\displaystyle\int^x_0\left(\displaystyle\sum\limits_{n=1}^\infty a_{n-1}t^{n-1}\right)\mathrm{d}t-x\left(\displaystyle\sum\limits_{n=1}^\infty a_{n}x^n+a_0\right)\\ &=\cfrac{5}{3}\displaystyle\int^x_0\left(\displaystyle\sum\limits_{n=1}^\infty a_{n}t^{n}+a_0\right)\mathrm{d}t-x\left(\displaystyle\sum\limits_{n=1}^\infty a_{n}x^n+a_0\right)\\ &=\cfrac{5}{3}\displaystyle\int^x_0[S(t)+3]\mathrm{d}t-x[S(x)+3]. \end{aligned} S(x)=n=1∑∞anxn=n=1∑∞n1(35−n)an−1xn=n=1∑∞n1(35an−1−nan−1)xn=35n=1∑∞n1an−1xn−n=1∑∞an−1xn=35∫0x(n=1∑∞n1an−1tn)′dt−xn=1∑∞an−1xn=35∫0x(n=1∑∞an−1tn−1)dt−x(n=1∑∞anxn+a0)=35∫0x(n=1∑∞antn+a0)dt−x(n=1∑∞anxn+a0)=35∫0x[S(t)+3]dt−x[S(x)+3].
对 S ( x ) S(x) S(x)求导,得 S ′ ( x ) = 5 3 [ S ( t ) + 3 ] d t − [ S ( x ) + 3 ] − x S ′ ( x ) S'(x)=\cfrac{5}{3}[S(t)+3]\mathrm{d}t-[S(x)+3]-xS'(x) S′(x)=35[S(t)+3]dt−[S(x)+3]−xS′(x),整理得
( 1 + x ) S ′ ( x ) = 2 3 [ S ( x ) + 3 ] ⇒ S ′ ( x ) S ( x ) + 3 = 2 3 ⋅ 1 1 + x ⇒ ln [ S ( x ) + 3 ] = 2 3 ln ( 1 + x ) + ln C ⇒ S ( x ) + 3 ( 1 + x ) 2 3 = C ⇒ S ( x ) = 3 ( 1 + x ) 2 3 − 3 , ∣ x ∣ < 1 \begin{aligned} &(1+x)S'(x)=\cfrac{2}{3}[S(x)+3]\\ \Rightarrow&\cfrac{S'(x)}{S(x)+3}=\cfrac{2}{3}\cdot\cfrac{1}{1+x}\\ \Rightarrow&\ln[S(x)+3]=\cfrac{2}{3}\ln(1+x)+\ln C\\ \Rightarrow&\cfrac{S(x)+3}{(1+x)^{\frac{2}{3}}}=C\\ \Rightarrow&S(x)=3(1+x)^{\frac{2}{3}}-3,|x|<1 \end{aligned} ⇒⇒⇒⇒(1+x)S′(x)=32[S(x)+3]S(x)+3S′(x)=32⋅1+x1ln[S(x)+3]=32ln(1+x)+lnC(1+x)32S(x)+3=CS(x)=3(1+x)32−3,∣x∣<1
(这道题主要利用了微分方程核比值判别法求解)
习题十三
13.5 讨论级数 ∑ n = 3 ∞ ( − 1 ) n ( n 2 − 3 n + 2 ) x \displaystyle\sum\limits_{n=3}^\infty\cfrac{(-1)^n}{(n^2-3n+2)^x} n=3∑∞(n2−3n+2)x(−1)n的敛散性, x x x为实数。
解 因为 ∣ u n ∣ = 1 ( n 2 − 3 n + 2 ) x ∼ 1 n 2 x ( n → ∞ ) |u_n|=\cfrac{1}{(n^2-3n+2)^x}\sim\cfrac{1}{n^{2x}}(n\to\infty) ∣un∣=(n2−3n+2)x1∼n2x1(n→∞),当 x > 0 x>0 x>0时, 1 n 2 x → + ∞ \cfrac{1}{n^{2x}}\to+\infty n2x1→+∞,故原级数发散;当 x = 0 x=0 x=0时, 1 n 2 x = 1 ≠ 0 \cfrac{1}{n^{2x}}=1\ne0 n2x1=1=0,故原级数发散;当 x > 1 2 x>\cfrac{1}{2} x>21时, ∑ n = 3 ∞ ( − 1 ) n ( n 2 − 3 n + 2 ) x \displaystyle\sum\limits_{n=3}^\infty\cfrac{(-1)^n}{(n^2-3n+2)^x} n=3∑∞(n2−3n+2)x(−1)n绝对收敛;当 0 < x ⩽ 1 2 0
新版例题十六
例16.1
例16.3
例16.8(4)
例16.13
例16.16
例16.21
例16.24
例16.30
例16.40
新版习题十六
16.1
16.8
写在最后
如果觉得文章不错就点个赞吧。另外,如果有不同的观点,欢迎留言或私信。
欢迎非商业转载,转载请注明出处。