5.5matlab曲线拟合（多项式函数拟合）
曲线拟合的三种功能:
(1)估算数据
(2)预测趋势
(3)总结规律
1、引例-人口预测问题
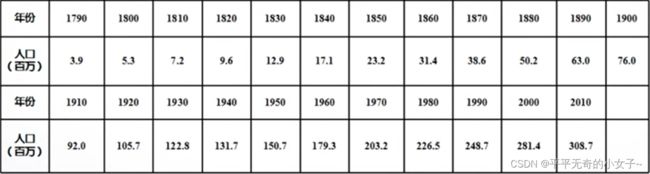
人口增长是当今世界上都关注的问题，对人口增长趋势进行预测是各国普遍的做法。已知某国1790年到2010年间历次人口普查数据如下表所示，请预测该国2020年的人口数。
解决思路:
找一个函数，去逼近这些数据，然后再根据找到的函数，计算预测点的值。
polyfit()： 用于建立多项式函数去逼近样本数据
x = 1790:10:2010; %时间向量
y = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 63 76 92 ...
105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4 308.7]; %人口向量
p = polyfit(x,y,3); %生成3次多项式函数，将系数向量保存在p中
polyval(p,2020) %计算该多项式函数在2020处的函数值,结果为339.8
plot(x,y,'*',x,polyval(p,x),'r')
legend('散点图','拟合曲线','location','southeast')
title('人口预测问题','color','r','fontsize',14)
2、曲线拟合的原理
与数据插值类似，曲线拟合也是一种函数逼近的方法。
在某种意义下达到最小。两个问题:
(1)用什么类型的函数做逼近函数?
多项式函数能够将复杂阃题简单化，表达能力强、计算方便、函数性态好。
(2）误差最小到底怎么计算?
最小二乘法（又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和来寻找数据的最佳函数匹配。
3、曲线拟合的实现方法
polyfit( ):多项式拟合函数。
函数功能:求得最小二乘拟合多项式系数。调用格式:
( 1) P=polyfit(X,Y,m)
( 2)[P,S]=polyfit(X,Y,m)
(3 )[P,S,mu]=polyfit(X,Y,m)
根据样本数据X和Y，产生一个m次多项式P及其在采样点误差数据S，mu是一个二元向量，mu(1)是mean(X)（平均值）,而mu(2)是std(X)（标准差）。
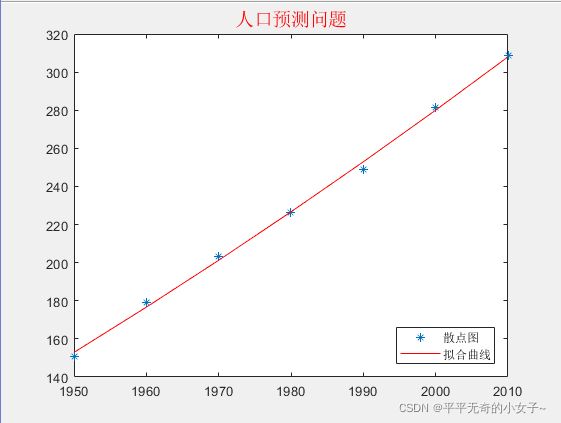
x = 1950:10:2010; %时间向量,二战后至今
y = [150.7 179.3 203.2 226.5 248.7 281.4 308.7]; %人口向量
p = polyfit(x,y,3); %生成3次多项式函数，将系数向量保存在p中，发现前两个系数为0，拟合次数太高
p = polyfit(x,y,2)
plot(x,y,'*',x,polyval(p,x),'r')
legend('散点图','拟合曲线','location','southeast')
title('人口预测问题','color','r','fontsize',14)
在利用曲线拟合解决实际问题时
（1）要对问题的背景进行详细的分析。
（2）采样点并非越多越好，适当的时候可以减少采样点,分段进行拟合。