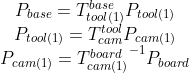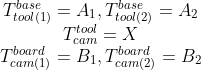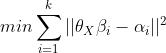标定学习笔记（四）-- 手眼标定详解

        本文主要介绍了机器人手眼标定的相关原理与思路，介绍了两种不同安装条件下如何通过同组固定点进行手眼标定，及通过解决  问题进行手眼标定，最后给出了手眼标定的相关评价方式。文章重在进行标定过程的梳理以及相关公式的推导，主要目的还是为了厘清什么是手眼标定，以及如何进行手眼标定。

        本文依旧作为自己学习的一些记录，如有谬误，欢迎斧正！

        文章参考资料：

        相机标定（一）：机器人手眼标定 - 知乎 (zhihu.com)

        手眼标定_全面细致的推导过程 (360doc.com)

        手眼标定传统方法 - 研究僧小陈 - 博客园 (cnblogs.com)

        手眼标定之基本原理_3D视觉工坊-CSDN博客_手眼标定

        手眼标定（Hand in Eye） - 简书 (jianshu.com)

---

1  如何理解手眼标定

        我们不妨想象，在生活中，我们需要用手移动某一物体时，需要经过哪些步骤？

        第一步：通过眼睛去观察三维世界，将三维世界的信息传递至视网膜，转换成二维平面的信息传递给我们的大脑；

        第二步：假设，当我们需要移动三维空间下的物体时，对我们的大脑而言，是将一个物体从二维平面的 A' 点移动至 B' 点，因此大脑需要计算从二维坐标转换到三维坐标 A 点和 B 点。

        第三步：当大脑获得了 A 点和 B 点的坐标，就可以用手将物体进行相应的移动。

        其中，第二步就是进行手眼标定，即得到二维坐标（像素坐标系）到三维坐标（世界坐标系）的转换矩阵。

        在实际的控制过程中，相机在检测到目标在图像中的像素位置后，通过标定好的坐标转换矩阵将相机的像素坐标变换到机械手的空间坐标系中，然后根据机械手坐标系计算出各个电机该如何运动，从而控制机械手到达指定位置。

2  坐标系与转换关系

2.1  基础坐标系

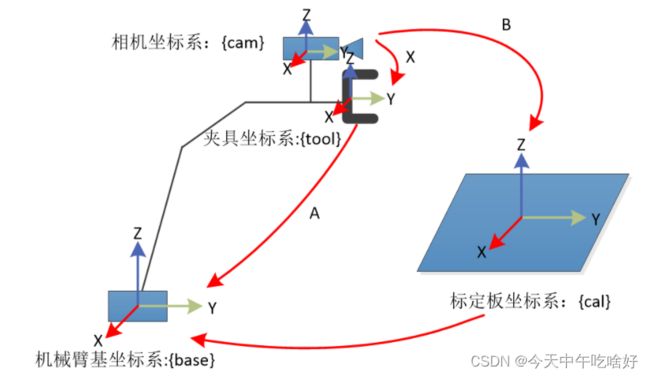
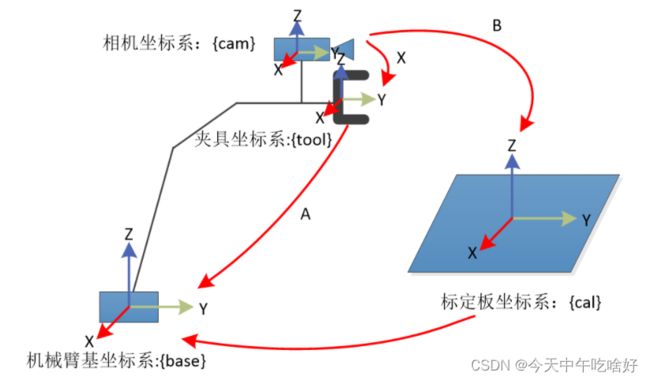
        对于上面的讲解我们将其推及一个简单的机械手系统，我们不难得知其中涉及的坐标系包括：

        1）机械手基础坐标系：

        2）机械手末端夹具坐标系：

        3）相机坐标系：

        由之前介绍的相机标定相关知识，我们也可以知道，这里说的相机坐标系不仅包括相机本身的坐标系，还包括像素坐标系。

        4）工件坐标系（标定板坐标系）：

2.2  坐标系转换关系

        坐标系之间的转换关系可以记为：

        1）机械手末端夹具坐标系到机械手基础坐标系的转换关系：

        该转换关系可以通过机器人系统得出，在手眼标定过程中我们认为其是已知的，其转换关系用矩阵进行表示可以记为： 。

        2）相机坐标系到机械手末端夹具坐标系的转换关系：

        尽管该转换关系视相机的装载方式有所区别，但相同点是我们认为其是未知的，也正是我们需要去进行求解的，其转换关系用矩阵进行表示可以记为： 。

        3）相机坐标系到标定板坐标系的转换关系：

        该转换关系我们可以通过相机标定进行获得，因此我们也认为其是已知的，其转换关系用矩阵进行表示可以记为： 。

        4）标定板坐标系到机械手基础坐标系的转换关系：

        该转换关系也正是我们最终希望求解的，只要机械手整体与标定板的相对位置不发生变化，这个变换矩阵也就不发生变化。

3  利用同组固定点进行标定

3.1  通用思路

        机器人的手眼标定其实就是两个坐标系之间的转换关系的标定。我们希望计算出相机坐标系到机械手坐标系的转换关系，并且我们已知对应的几个固定点 在这两个坐标系的坐标 和  。根据坐标转换公式，可以得出：

        上式中的  表示我们希望计算出的相机到机械手的转换矩阵。

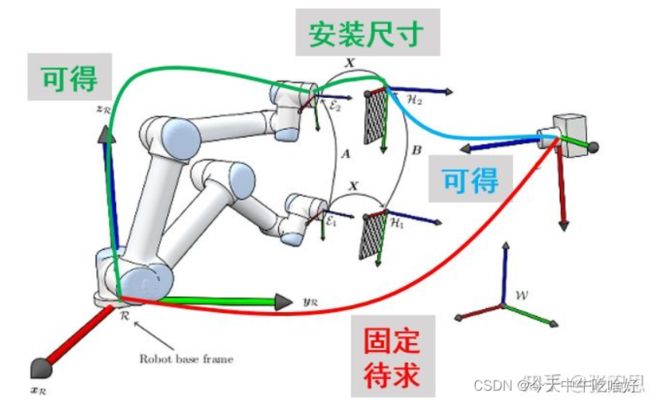
3.2  相机不在机械手上（eye to hand）

3.2.1  待求量

        相机固定在一个地方，机械手的运动不会带着相机一起移动。对于 Eye-to-Hand 而言，相机坐标系相对于机械手基础坐标系是固定的，而对于机械手末端夹具坐标系是变化的。

        在 Eye-to-Hand 的问题下，待求量为相机到机械手基座坐标系的固定转换矩阵  。考虑到相机是固定在一个位置，因此相机只有相对于基座坐标系才是固定不变的，这样我们的待求量 是一个固定的参数，这样的标定才是有意义的。

3.2.2  标定思路

        根据 第3.1节 中所介绍的通用求解思路，下一步需要通过棋盘格图像上的固定点  来获得机械手基座坐标系下的固定点坐标  和相机坐标系下的坐标 。

        通过识别棋盘格，我们可以得到棋盘格中的角点在相机坐标系下的坐标 ，但是这是二维坐标，通过相机内参和物体的深度信息我们可以计算出 。接下来我们只要测量出来对应的棋盘格点在机械手基座坐标系下的坐标 ，便可以标定出机械手和相机之间的转换矩阵 。

3.2.3  转换关系推导

        在 Eye-to-Hand 问题下，棋盘格在标定的时候，会固定在机械手的末端夹具上，而机械手的末端夹具坐标系到基座坐标系的转换矩阵，可以通过机器人正向运动学计算得到。因此我们可以通过如下关系测量出棋盘格点在机器人基座坐标系下的坐标  ：

        在上述公式中， 和  分别代表机械手末端夹具坐标系(tool)到基座坐标系(base)的转换矩阵和棋盘格坐标系(board)到机械手末端夹具坐标系(tool)的转换矩阵。

        其中， 可以实时根据机器人正向运动学得到，而  可以通过设计一个固定尺寸的棋盘格得到。当棋盘格尺寸以及安装固定后，我们可以设棋盘格的左上角点为原点，然后通过测量或者设计尺寸计算棋盘格原点到机器人末端坐标原点的平移坐标，而棋盘格平面一般与机械手末端载具平面平行，因此该原点的法向量也可以获得，接下来就可以计算出  。

         代表棋盘格角点再棋盘格坐标系下的坐标，这个同样可以根据设计棋盘格的尺寸得到。需要注意的是棋盘格的角点在机器人坐标系和图像坐标系的顺序需要一一对应，但是一般的方形棋盘格会存在旋转对称的问题，即我们无法区分棋盘格的原点是在左上角还是右下角，因此在进行手眼标定时可以使用非对称的棋盘格。

        通过上面的推导，我们已经可以计算出棋盘格角点在机器人基座坐标系中的坐标 ，然后根据张正友标定法得到棋盘格在相机坐标系中的坐标 。那么根据 第3.1节 中介绍的计算方法就可以得到相机到机器人的转换矩阵：

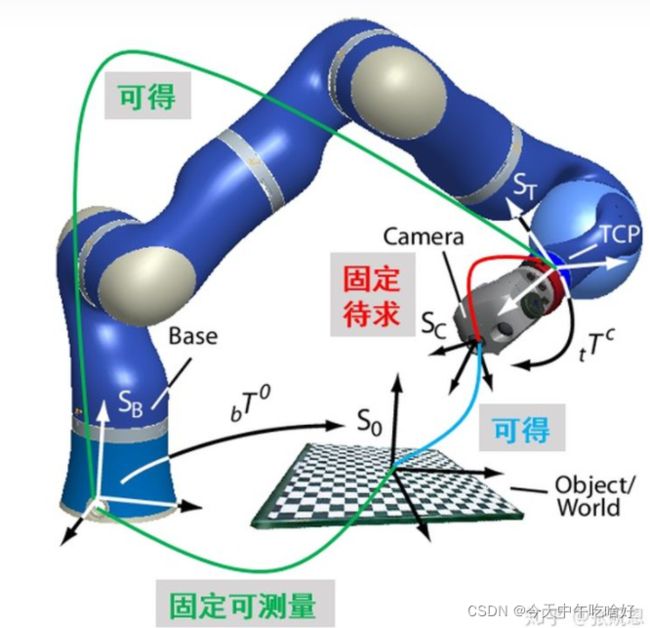
3.3  相机在机械手上（eye in hand）

3.3.1  待求量

        相机安装在机械手上，随着机械手一起移动。对于 Eye-in-Hand 而言，相机坐标系相对于机械手末端夹具坐标系是固定的，而对于机械手基础坐标系是变化的。

        当相机固定于机械手末端夹具时，此时相机坐标系与机械手末端夹具坐标系的变换关系固定，而与基座坐标系的变换关系会时刻变化，因此此时的待求量变成了相机坐标系(camera)到机械手末端载具坐标系(tool)的变换矩阵 。

3.3.2  转换关系推导

        根据各个坐标系的关系，我们可以给出下述的坐标变换方程：

        上式中  代表固定在某个位置上的棋盘格中的角点，在机器人基座坐标系下的坐标。可以通过两种方式计算这个坐标：

        1）在机械手末端的夹具上加上探针，直接由末端去触碰棋盘格上的点，根据机器人正向运动学得到的末端夹具到基座坐标系的转换矩阵  及棋盘格角点到末端坐标系的坐标 ，我们可以得到固定的棋盘格角点在机器人基座坐标系下的坐标  。

        2）在机械手末端的夹具上安装相机，由相机去直接测量棋盘格角点机器对应的坐标 ，通过计算机器手末端夹具到基座坐标系的转换矩阵  和相机坐标系到机器人末端坐标系的转换矩阵 ，便可以求出棋盘格在机器人基座坐标系下的坐标 。

        在第二种方式中，相机坐标系到机器人末端坐标系的转换矩阵  是我们的待求量，因此我们需要对开始时描述的坐标变换方程进行简单的变换：

        在上式中，坐标的三个变量都是已知量，由此我们可以计算出相机到机器人末端坐标系的转换矩阵 。

3.4  小结

        本部分所探讨的标定方法其实是最直接的方式，即尽量测量出同一组点在不同坐标系下的坐标，从而直接可以通过伪逆矩阵的方式计算出坐标变换矩阵。当然，还有更加具有普适性的方法，在不满足上述条件下的情况也可以标定出矩阵，也就是经典的  问题的求解，其中 ，已知，为待求量。这种方法将在下章进行讨论。

4   问题推导

4.1  转换关系推导（以Eye-in-Hand为例）

        首先，我们控制机械手从初始位置移动至位置 1 ，我们可以获取此时的机械臂基座坐标，夹具坐标，相机坐标以及标定板坐标：

        对上面的三个公式进行联立，我们可以得出：

        同理，将机械手移动到位置 2 时，可以得出：

        在 Eye-in-Hand 问题中，机械臂基座与标定板之间的关系是固定的，所以可得：

        在 Eye-in-Hand 问题中，待求量为机械臂末端夹具坐标系到相机坐标系的转换关系，我们不妨记：

        因此，上面的推导公式可以写做：

        令

        则上面的推导公式又可以简写为：

        至此，我们可以将手眼标定问题归结为对上述公式中  的求解问题。其中， 可以通过机器人正向运动学获得， 可以通过相机标定获得。

4.2  求解 

        求解  问题的方式有很多种，包括但不限于：利用李群理论，转化为最小二乘问题和采用时对偶四元数的知识，进行统一计算。下面主要介绍使用李群李代数求解的方法。

        李代数到李群的转换满足指数映射关系，假设  ，而  ，则其指数映射满足罗德里格斯公式：

        其中  ，需要注意的是，正常的指数映射不是这种形式。

        将  写成矩阵形式为：

        展开上述矩阵可得：

        对于上述方程我们可以采用两步法进行求解，即先解算旋转矩阵，再求解平移向量。

4.2.1  求解旋转矩阵

        假设 ，这里的矩阵都是旋转矩阵(SO(3))，而非变换矩阵(SE(3))。

        通过变换可得：

        方程两边取对数可得：

        令：

        则上式可化为：

        从而可化为：

        当存在多组观测值时，求解该方程可以转化为下面最小二乘拟合问题：

        显然，上述问题是典型的绝对定向问题，因而求解上式与绝对定向相同，其解为：

        其中，

        上式仅在  不奇异时可以进行求解，当只有两组 ， 时，不能使用上述方法进行求解。

        当只有两组 ， 时，即存在  时：

        其中：

        综上所述，可以计算出旋转矩阵。

4.2.2  求解平移向量

        已知：

        通过移项化简可得：

        不妨写作：

        又因为  不一定可逆，因此在等式两边同时乘以 ，即：

        由此可知：

        当存在多组数据时：

        即可求得  。

4.3  小结

        通过解决  问题进行手眼标定的方法，其步骤大致如下：

        1）当机器人静止在 位置1 时，进行摄像机标定，获得此时的外参矩阵 ；

        2）控制机器人移动至 位置2 ，获取此时的机器人正向运动矩阵 ；

        3）当机器人静止在 位置2 时，进行摄像机标定，获得此时的外参矩阵 ；

        4）控制机器人移动至 位置3 ，获取此时的机器人正向运动矩阵 ；

        5）当机器人静止在 位置2 时，进行摄像机标定，获得此时的外参矩阵 ；

……测量多组数据……

        n）根据测量得到的数据，求解 。

5  评价手眼标定效果

        通过测量几组不同位置的目标点，我们可以比较：

        测量值：

        和预测值： 

        之间的距离误差：

        通过计算各个点的误差的均值和标准差，最终我们可以计算出标定结果的系统误差（均值）和随机误差（标准差）。