torch.nn.LocalResponseNorm（局部响应归一化）详解（附源码解析）

torch.nn.LocalResponseNorm

局部响应归一化的理解

局部归一化的动机：在神经生物学有一个概念叫做侧抑制(lateral inhibitio)，指的是被激活的神经元抑制相邻神经元。归一化的目的是“抑制”，局部响应归一化就是借鉴侧抑制的思想来实现局部控制，尤其当我们使用RELU的时候这种”侧抑制“很管用。

也就是说你可以理解为对一个位置的值进行变形，变形的结果是该位置的值占邻域内的全部值的一个抽象的比重。

好处：有利于增加泛化能力，做了平滑处理，识别率提高1-2%。LRN层模仿生物神经系统的侧抑制机制，对局部神经元的活动创建竞争机制，使得响应比较大的值相对更大，提高模型泛化能力。Hinton在Imagenet中表明分别提升1.4%和1.2%。

---

LocalResponseNorm参数讲解

torch.nn.LocalResponseNorm(size, alpha=0.0001, beta=0.75, k=1.0)

$$b_{x,y}^i=a_{x,y}^i/{\left(k+\frac{\alpha }{size}\sum _{j=max(0,i-size//2)}^{min(C-1,i+(size-1)//2)}(a_{x,y}^j{)}^2\right)}^{\beta }$$

简单解释一下公式：

• 输入为$(N,C,W,H)$时，即四维的第一维表示样本数，第二维表示通道数，第三四维表示宽高；

• 输出与输入维度个数及维度大小相同；

• $\alpha$就是参数alpha，$\beta$就是参数beta，$k$就是参数k，$size$就是参数size；

• $i$和$j$分别表示第$i$和第$j$个通道，$x$和$y$分别表示宽高维度上的位置；

• 注意公式中$min$中的$C$就是$(N,C,W,H)$中的$C$，符号$//$表示整除。

参数详解：

• size：表示对一个位置的值进行局部响应归一化需要涉及的邻域通道的个数。比如size=3，则当$i=0$时上述公式中的$j$的变化范围是$[0,1]$，也就是说涉及的通道为第0个通道和第1个通道；当$i=1$时$j$的变化范围是$[0,2]$，涉及通道为第0、1、2个通道。（详细理解需要看下面对“实现方式”的讲解）

• alpha：见公式，系数。

• beta：见公式，指数。

• k：见公式，作用是防止发生除0的情况。

---

图文讲解过程

LRN 根据归一化方向不同有两种形式，分别为 $Inter-ChannelLRN$ 和 $Intra-ChannelLRN$：

因为AlexNet中和PyTorch中都是实现的第一种（$Inter-ChannelLRN$），即在通道这一维度上进行局部响应归一化，也就是对于每一个位置的变形后的值都由其相邻通道内对应位置的值决定，所以我们只讲第一种。而第二种（$Intra-ChannelLRN$）则是在同一个通道内进行局部响应，即每个通道内的像素值与同通道内的相邻像素值有关，不做过多的讲解。

• Inter-Channel LRN Example

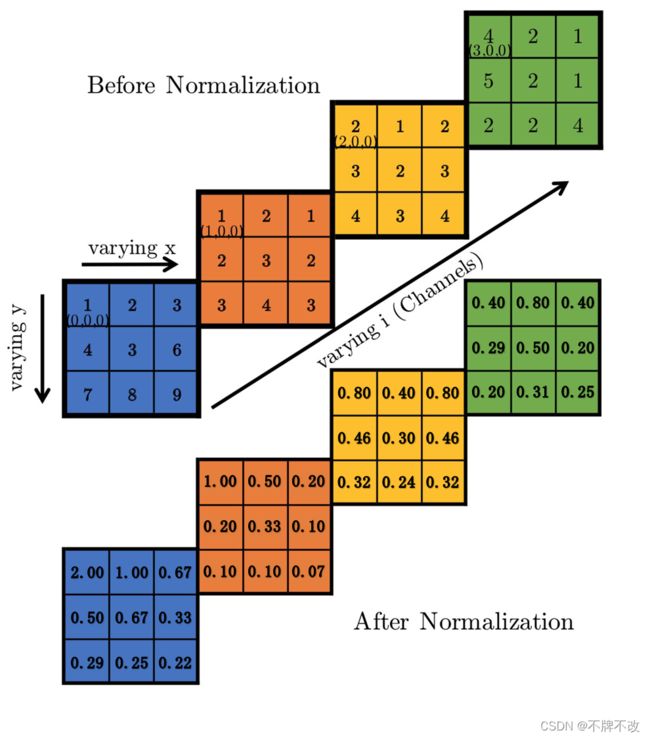
假设输入为$(1,4,3,3)$，如下图。设置参数size=2，alpha=1，beta=1，k=0，则计算过程如下。

在计算第一个通道的第一个元素局部响应归一化后的值时，因为$j$的下限是$max(0,i-size//2)=max(0,-1)=0$，上限是$i+(size-1)//2=i=0$，所以需要考虑的通道仅为第0通道，即仅与(0,0,0)处的1有关，代入公式得到$b=1/(0+\frac{1}{2}\times (1^2))=2.00$。

再看(1,0,0)位置的1响应后的值，$j$的范围是$[0,1]$，所以需要考虑的通道为第0通道和第1通道，即与(0,0,0)处的1和(1,0,0)处的1有关，代入公式得到$b=1/(0+\frac{1}{2}\times (1^2+1^2))=1.00$。

其他以此类推。

---

PyTorch中对LocalResponseNorm函数的实现

这部分是重点，详细解析源码。

源码：

def local_response_norm(input, size, alpha=1e-4, beta=0.75, k=1.):
    # type: (Tensor, int, float, float, float) -> Tensor
    r"""Applies local response normalization over an input signal composed of
    several input planes, where channels occupy the second dimension.
    Applies normalization across channels.

    See :class:`~torch.nn.LocalResponseNorm` for details.
    """
    if not torch.jit.is_scripting():
        if type(input) is not Tensor and has_torch_function((input,)):
            return handle_torch_function(
                local_response_norm, (input,), input, size, alpha=alpha, beta=beta, k=k)
    dim = input.dim() # 重点！
    if dim < 3:
        raise ValueError('Expected 3D or higher dimensionality \
                         input (got {} dimensions)'.format(dim))
    div = input.mul(input).unsqueeze(1) # 重点！
    if dim == 3:
        div = pad(div, (0, 0, size // 2, (size - 1) // 2))
        div = avg_pool2d(div, (size, 1), stride=1).squeeze(1)
    else: # 重点！
        sizes = input.size() # 重点！
        div = div.view(sizes[0], 1, sizes[1], sizes[2], -1) # 重点！
        div = pad(div, (0, 0, 0, 0, size // 2, (size - 1) // 2)) # 重点！
        div = avg_pool3d(div, (size, 1, 1), stride=1).squeeze(1) # 重点！
        div = div.view(sizes) # 重点！
    div = div.mul(alpha).add(k).pow(beta) # 重点！
    return input / div # 重点！

需要注意的就只有注释“重点！”的几条语句。只讲解四维输入的情况，即输入为$(N,C,W,H)$。

---

先规定我们的输入是（图文中的样例）：

import torch
import torch.nn as nn

c1 = [[1,2,3], [4,3,6], [7,8,9]]
c2 = [[1,2,1], [2,3,2], [3,4,3]]
c3 = [[2,1,2], [3,2,3], [4,3,4]]
c4 = [[4,2,1], [5,2,1], [2,2,4]]
x = torch.tensor([[c1, c2, c3, c4]], dtype=torch.float32)

print(x.size())
print(x)
"""
torch.Size([1, 4, 3, 3])
tensor([[[[1., 2., 3.],
          [4., 3., 6.],
          [7., 8., 9.]],

         [[1., 2., 1.],
          [2., 3., 2.],
          [3., 4., 3.]],

         [[2., 1., 2.],
          [3., 2., 3.],
          [4., 3., 4.]],

         [[4., 2., 1.],
          [5., 2., 1.],
          [2., 2., 4.]]]])
"""

---

从第一句看起：

dim = input.dim() # 重点！

这步是获取输入的维度。如果是四维，则会到else语句。

---

再看下一步：

div = input.mul(input).unsqueeze(1)

可以理解div为临时变量，现在div保存的是我们输入的四维张量进行按位平方操作，之后再在dim=1的维度进行扩充。

首先要明白.unsqueeze(1)是在干什么：

import torch

input = torch.ones(1, 4, 3, 3, dtype=torch.float32)
print(input.size())
print(input)
"""
torch.Size([1, 4, 3, 3])
tensor([[[[1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.]],

         [[1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.]],

         [[1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.]],

         [[1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.]]]])
"""

如果对input调用.unsqueeze(1)：

print(input.unsqueeze(dim=1).size())
print(input.unsqueeze(dim=1))
"""
torch.Size([1, 1, 4, 3, 3])
tensor([[[[[1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.]],

          [[1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.]],

          [[1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.]],

          [[1., 1., 1.],
           [1., 1., 1.],
           [1., 1., 1.]]]]])
"""

发现只是在dim=1多插入了一维，其他没有变化。

如果调用.unsqueeze(0)和调用.unsqueeze(4)：

print(input.unsqueeze(dim=0).size())
print(input.unsqueeze(dim=4).size())
"""
torch.Size([1, 1, 4, 3, 3])
torch.Size([1, 4, 3, 3, 1])
"""

就是起到扩充维度个数的作用。

---

言归正传，div = input.mul(input).unsqueeze(1)语句就是将输入的四维张量input先进行平方再进行扩维。

以上图中举的样例作为输入，执行该步得到的输出为：（对源码稍微修改一下，在该语句后加上个print就可以观察输出了）

import torch
import torch.nn as nn

lrn = nn.LocalResponseNorm(size=2, alpha=1, beta=1, k=0)

c1 = [[1,2,3], [4,3,6], [7,8,9]]
c2 = [[1,2,1], [2,3,2], [3,4,3]]
c3 = [[2,1,2], [3,2,3], [4,3,4]]
c4 = [[4,2,1], [5,2,1], [2,2,4]]
x = torch.tensor([[c1, c2, c3, c4]], dtype=torch.float32)
lrn(x)
"""
torch.Size([1, 1, 4, 3, 3]) # 扩充维度
tensor([[[[[ 1.,  4.,  9.],
           [16.,  9., 36.],
           [49., 64., 81.]],

          [[ 1.,  4.,  1.],
           [ 4.,  9.,  4.],
           [ 9., 16.,  9.]],

          [[ 4.,  1.,  4.],
           [ 9.,  4.,  9.],
           [16.,  9., 16.]],

          [[16.,  4.,  1.],
           [25.,  4.,  1.],
           [ 4.,  4., 16.]]]]]) # 平方
"""

---

进入else，只看维度在三维以上的情况。else中的第一句是：

sizes = input.size()

获取输入张量的各个维度的大小。

---

再下一句：

div = div.view(sizes[0], 1, sizes[1], sizes[2], -1)

对五维张量div进行变形，第二维度大小变为1，由于上面.unsqueeze(1)变换的就是第二维度，所以该语句对div没有影响。（应该是在其他情况下会有影响）

---

再看下一句：

div = pad(div, (0, 0, 0, 0, size // 2, (size - 1) // 2))

这句话是为div加上padding，至于怎么加，先假设div的五个维度为$(N,New,C,W,H)$，在$C$这一维度的最前面插入$size//2$个大小为$(W,H)$的全零padding，在$C$这一维度的最后面插入$(size-1)//2$个大小为$(W,H)$的全零padding。

还是对于上面的输入张量而言，如果我们规定size=2，则该语句执行后的输出如下：

"""
tensor([[[[[ 0.,  0.,  0.],
           [ 0.,  0.,  0.],
           [ 0.,  0.,  0.]],

          [[ 1.,  4.,  9.],
           [16.,  9., 36.],
           [49., 64., 81.]],

          [[ 1.,  4.,  1.],
           [ 4.,  9.,  4.],
           [ 9., 16.,  9.]],

          [[ 4.,  1.,  4.],
           [ 9.,  4.,  9.],
           [16.,  9., 16.]],

          [[16.,  4.,  1.],
           [25.,  4.,  1.],
           [ 4.,  4., 16.]]]]])
"""

size=2，所以前面要插入1个padding，后面要插入0个padding，没有问题。

如果size=3，则输出如下：

"""
tensor([[[[[ 0.,  0.,  0.],
           [ 0.,  0.,  0.],
           [ 0.,  0.,  0.]],

          [[ 1.,  4.,  9.],
           [16.,  9., 36.],
           [49., 64., 81.]],

          [[ 1.,  4.,  1.],
           [ 4.,  9.,  4.],
           [ 9., 16.,  9.]],

          [[ 4.,  1.,  4.],
           [ 9.,  4.,  9.],
           [16.,  9., 16.]],

          [[16.,  4.,  1.],
           [25.,  4.,  1.],
           [ 4.,  4., 16.]],

          [[ 0.,  0.,  0.],
           [ 0.,  0.,  0.],
           [ 0.,  0.,  0.]]]]])
"""

根据整除计算的结果也可以算出前面、后面均插入一个padding。

---

再看下一条语句：

div = avg_pool3d(div, (size, 1, 1), stride=1).squeeze(1)

该语句进行三维平均池化操作，再进行.unsqueeze(1)的逆操作。

二维平均池化我们都知道是计算${\sum }_{m=W_0}^{W_1}{\sum }_{n=H_0}^{H_1}input$，也就是一个样本的一个通道的一块区域（二维，理解为一个面内）像素值的均值。

类似地，三维平均池化是对于一个五维张量$(N,C,D,W,H)$而言的，是计算${\sum }_{k=D_0}^{D_1}{\sum }_{m=W_0}^{W_1}{\sum }_{n=H_0}^{H_1}input$，也就是一个样本的一个通道的一块区域（三维，理解为一个体内）像素值的均值。

我们知道了.unsqueeze(1)是加一个维度，那么.squeeze(1)就是删去dim=1这一维度，对咱们的样例没有影响。

注意是对加入padding后的五维张量进行操作。

仍以size=2为例：（前面加入一个padding，后面不加）

假设灰色部分为padding部分，即全0；紫色、绿色、粉色依次为原先的第一、二、三通道。

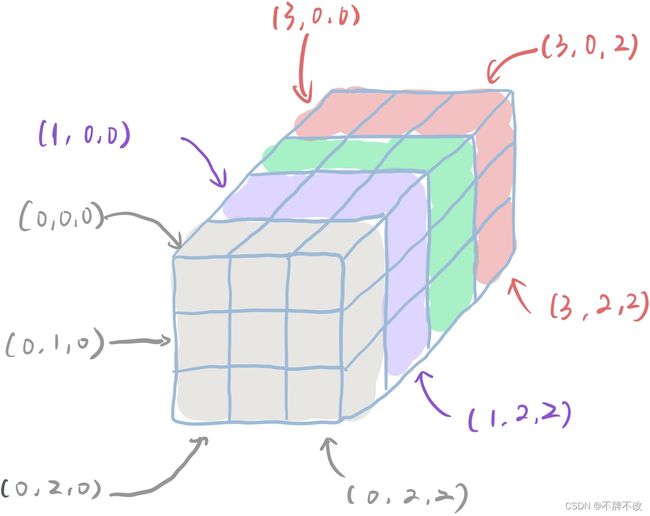
进行三维平均池化的窗口大小为$(size,1,1)$，所以对于(0,0,0)位置的池化操作为(div(0,0,0) + div(1, 0, 0))/2，对(1,0,0)位置的池化为(div(1, 0, 0) + div(2, 0, 0))/2，对(2,0,0)位置的池化为(div(2, 0, 0) + div(3, 0, 0))/2，由于(3,0,0)后面就没有通道了，所以(X,0,0)位置的池化就没有了。其他位置同理。

对于该样例，输出一下该语句执行完的结果：

size=2时
进行池化前：
"""
tensor([[[[[ 0.,  0.,  0.],
           [ 0.,  0.,  0.],
           [ 0.,  0.,  0.]],

          [[ 1.,  4.,  9.],
           [16.,  9., 36.],
           [49., 64., 81.]],

          [[ 1.,  4.,  1.],
           [ 4.,  9.,  4.],
           [ 9., 16.,  9.]],

          [[ 4.,  1.,  4.],
           [ 9.,  4.,  9.],
           [16.,  9., 16.]],

          [[16.,  4.,  1.],
           [25.,  4.,  1.],
           [ 4.,  4., 16.]]]]])
"""
进行池化后：
"""
tensor([[[[ 0.5000,  2.0000,  4.5000],
          [ 8.0000,  4.5000, 18.0000],
          [24.5000, 32.0000, 40.5000]],

         [[ 1.0000,  4.0000,  5.0000],
          [10.0000,  9.0000, 20.0000],
          [29.0000, 40.0000, 45.0000]],

         [[ 2.5000,  2.5000,  2.5000],
          [ 6.5000,  6.5000,  6.5000],
          [12.5000, 12.5000, 12.5000]],

         [[10.0000,  2.5000,  2.5000],
          [17.0000,  4.0000,  5.0000],
          [10.0000,  6.5000, 16.0000]]]])
"""

验证一下，(0,0,0)的值变成了(1+0)/2=0.5。（多验证几个）没问题。

有能力的也可以试试输出当size=3时的池化结果，也就是前后都加了一个padding。

---

再看下一条语句：

div = div.view(sizes)

将池化后的结果变回原来的样式。其实我们上一步的.squeeze(1)已经将div变回去了。

---

再看下一条语句：

div = div.mul(alpha).add(k).pow(beta)

上述语句相当于已经计算出公式中的
$$\sum _{j=max(0,i-size//2)}^{min(C-1,i+(size-1)//2)}(a_{x,y}^j{)}^2$$
这一部分，所以该语句就是将其余的部分算上。

先每一个位置都乘以$\alpha$，再加上$k$，进行幂操作。

---

最后返回return input / div，原张量除以上面计算得到的分母，整个公式计算完成。

最后的输出：

"""
tensor([[[[2.0000, 1.0000, 0.6667],
          [0.5000, 0.6667, 0.3333],
          [0.2857, 0.2500, 0.2222]],

         [[1.0000, 0.5000, 0.2000],
          [0.2000, 0.3333, 0.1000],
          [0.1034, 0.1000, 0.0667]],

         [[0.8000, 0.4000, 0.8000],
          [0.4615, 0.3077, 0.4615],
          [0.3200, 0.2400, 0.3200]],

         [[0.4000, 0.8000, 0.4000],
          [0.2941, 0.5000, 0.2000],
          [0.2000, 0.3077, 0.2500]]]])
"""

总结一下，PyTorch实现该函数的重点思路是先在前面、后面分别加上$size//2$和$(size-1)//2$个padding，再以$(size,1,1)$为窗口进行3D池化，中间过程加上各种运算即可。