深度学习实战01-卷积神经网络(CNN)实现Mnist手写体识别
一、前期工作
1. 检查是否有可用的gpu
import tensorflow as tf
print("Num of GPUs available: ", len(tf.test.gpu_device_name()))
![]()
2. 导入数据
# 导入数据
import tensorflow as tf
from tensorflow.python.keras import datasets, layers, models
import matplotlib.pyplot as plt
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()
3. 数据归一化
归一化与标准化是特征缩放的两种形式,作用如下:
- 使不同量纲的特征处于同一数量级,减少方差大的特征的影响,使模型更准确。
- 加快学习算法的收敛速度。
详细介绍
归一化是将数据“拍扁”统一到区间(仅由极值决定),标准化是更加“弹性”和“动态”的,和整体样本的分布有很大的关系。
- 归一化:把数变为(0,1)之间的小数;缩放仅仅跟最大、最小值的差别有关。
- 标准化:将数据按比例缩放,使之落入一个小的特定区间;缩放与每个点都有关。
归一化(Normalization)
一般来说用的是min-max归一化,缩放到0-1之间,即:
![]()
对于图片来说,由于max是255,min是0,也就是直接除以255就可以完成归一化。
代码实现:
train_images, test_images = train_images/255.0, test_images/255.0
为什么要进行归一化
不归一化处理时,如果特征值较大时,梯度值也会较大,特征值较小时,梯度值也会较小。在模型反向传播时,梯度值更新与学习率一样,当学习率较小时,梯度值较小会导致更新缓慢,当学习率较大时,梯度值较大会导致模型不易收敛,因此为了使模型训练收敛平稳,对图像进行归一化操作,把不同维度的特征值调整到相近的范围内,就可以采用统一的学习率加速模型训练。
标准化的介绍
将数据变换成均值为0,标准差为1的分布(但不一定为正态分布):
![]()
代码实现:
transforms.Normalize(mean = (0.485, 0.456, 0.406), std = (0.299, 0.224, 0.225))
为什么要进行标准化
提升模型的泛化能力。
参考文章:
https://www.zhihu.com/question/20455227
https://www.zhihu.com/question/20467170
https://blog.csdn.net/qq_40714949/article/details/115267174
归一化处理
# 将像素的值标准化0到1的区间内:
train_images, test_images = train_images / 255.0, test_images / 255.0
train_images.shape, test_images.shape, train_labels.shape, test_labels.shape
# 输出结果:((60000, 28, 28), (10000, 28, 28), (60000,), (10000,))
4. 可视化图片
# 可视化图片
plt.figure(figsize=(20, 10))
for i in range(20):
plt.subplot(5, 10, i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(train_labels[i])
plt.show()
![]()
5. 调整图片格式
# 调整数据到我们需要的格式
train_images = train_images.reshape((60000, 28, 28, 1))
test_images = test_images.reshape((10000, 28, 28, 1))
train_images.shape, test_images.shape, train_labels.shape, test_labels.shape
# 运行结果:((60000, 28, 28, 1), (10000, 28, 28, 1), (60000,), (10000,))
二、构建CNN网络模型
model = models.Sequential([
layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)), # 卷积层1,卷积核3*3
layers.MaxPooling2D((2, 2)), # 池化层1, 2*2采样
layers.Conv2D(64, (3, 3), activation='relu'), # 卷积层2, 卷积核3*3
layers.MaxPooling2D((2, 2)), # 池化层2, 2*2采样
layers.Flatten(), # Flatten层,连接卷积层与全连接层
layers.Dense(64, activation='relu'), # 全连接层,特征进一步提取
layers.Dense(10) # 输出层,输出预期结果
])
# 打印网络结构
model.summary()
![]()
三、编译模型
此处设置优化器、损失函数
优化器(optimizer)
优化器就是在深度学习反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让损失函数(目标函数)值不断逼近全局最小。
参考文章:
https://zhuanlan.zhihu.com/p/261695487
损失函数
损失函数就是用来评价模型的预测值和真实值不一样的程度,当损失值越小,证明预计值越接近真实值,模型的训练程度就越好。为了让预测值 y^ (i) 尽量接近于真实值 y(i) ,学者提出了多个方法进行计算损失值,最常见的损失函数有均方误差(MSE)、交叉熵误差(CEE)等。
参考文章:
https://www.cnblogs.com/leslies2/p/14832685.html#p2
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
四、训练模型
设置输入的训练数据集(图片及标签)、验证数据集(图片及标签)以及迭代次数epochs
history = model.fit(train_images, train_labels, epochs=10, validation_data=(test_images, test_labels))
![]()
五、预测
通过下面的网络结构我们可以简单的理解为,输入一张图片,将会得到一组数据,这组代表这张图片上的数字为0-9中每一个数字的概率,输出的数字越大,可能性就越大。
![]()
plt.imshow(test_images[1])
![]()
# 输出测试集中第一张图片的预测结果
pre = model.predict(test_images) # 对所有测试图片进行预测
pre[1] # 输出第一张图片的预测结果
![]()
plt.imshow(test_images[2])
pre[2]
![]()
plt.imshow(test_images[3])
pre[3]
![]()
plt.imshow(test_images[10])
pre[10]
![]()
六、知识点详解
本文使用的是最简单的CNN模型——LeNet-5。
1. Mnist手写数字数据集介绍
Mnist手写数字数据集来源于美国国家标准与技术研究所,是著名的公开数据集之一。数据集中的数字图片是由250个不同职业的人纯手写绘制,数据集获取网址:http://yann.lecun.com/exdb/mnist/。我们一般采用如下方式直接调用数据集,而无需下载。
(train_images, train_labels),(test_images, test_labels) = datasets.mnist.load_data()
Mnist手写数字数据集中包含了70000张手写数字图片,其中60000张为训练数据,10000张为测试数据,70000张图片大小均是28x28像素,数据集样本如下:
![]()
如果我们把每一张图片中的像素转换为向量,则得到长度为28*28=784的向量。因此我们可以把训练集看成是是一个**[60000, 784]的张量,第一个维度表示图片的索引,第二个维度表示每张图片中的像素点。而图片里的每个像素点的值介于0-1**之间。
![]()
2. 神经网络程序说明
神经网络程序可简单概括如下:
![]()
3. 网络结构说明
- 模型结构
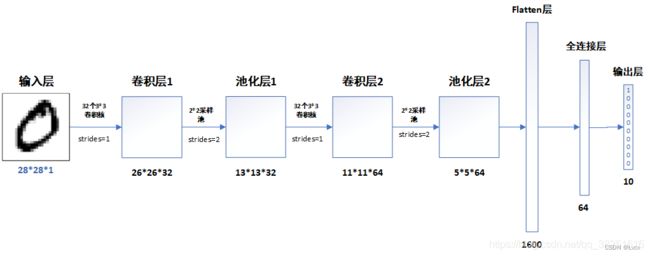
- 各层的作用
- 输入层:用于将数据输入到训练网络
- 卷积层:使用卷积核提取图片特征
- 池化层:进行下采样,用更高层的抽象表示图像特征
- Flatten层:将多维的输入一维化,常用在卷积层到全连接层的过渡
- 全连接层:起到“特征提取器”的作用
- 输出层:输出结果
参考文章:https://mtyjkh.blog.csdn.net/article/details/116920825