机器学习读书笔记:决策树
文章目录
- 如何形成一颗决策树
- 划分选择
-
- 信息熵 & 信息增益
- 基尼指数
- 剪枝
-
- 预剪枝
- 后剪枝
- 连续值 & 属性缺失处理
-
- 连续值
- 属性缺失
- 多变量决策树
如何形成一颗决策树
决策树从结构上来说就是一颗树的数据结构。从根节点开始,每次根据样本中的某个属性就行判断进行分岔,直到叶节点获得分类:
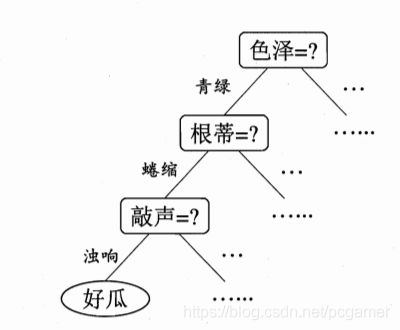
先理解一下这个递归函数的三个返回条件:
-
样本集 D D D中的样本全部属于同一个类别。就算样本集合 D D D中的属性有不同的取值,但是已经无法为当前的节点进行分岔了,所以就可以把这个作为叶子节点了。
-
A = ∅ A=\empty A=∅,表示可以属性全部划分过了,没法划分了。自然这个节点就只能成为叶子节点,类别以占比多的类别样本来确定。
-
样本集合 D D D在属性 A A A上全部相同。就比如可能会获得这样的样本,因为可能还有其他属性来确定类别,只是我们没发现而已:
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:好瓜 )
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:不是好瓜 )
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:好瓜 )
那么,此时也没法进行分类的,直接将这个节点作为叶子节点就行了,这个叶子节点的类型就取好瓜(先验分布)。
-
D v D_v Dv为空,表示根据某个属性 a a a进行划分后, a = a i a=a_i a=ai的属性值在样本集中没有。
就拿这个样本集来看:
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:好瓜 )
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:不是好瓜 )
(色泽 = 青绿,敲声 = 浊响,根蒂 = 蜷缩:好瓜 )
假设敲声还有“清脆”的取值,根据敲声来划分的话,那么 敲声 = “清脆”的样本集 D v D_v Dv是为空的。此时,将这个节点的类别设置成父节点的类别(书上说的是采用先验分布,我的理解是根据某个属性取值没有样本做判断,那就以父节点的为准)。
划分选择
在上面代码的第8行中,从属性集中选择某一个属性作为划分属性,这句话是决定决策树算法的关键所在。想象一下,如果选出来的属性没法很好的对样本集进行划分的话,会导致决策树的收敛会比较慢,或者说决策树的高度会比较高。理想中的划分应该是类似于二分查找的性能,第一次划分就可以将样本集中最大区别的那个属性挑出来,划分之后的节点中样本的“纯度”就会相对比较高。然后再根据这个原则继续划分。
那么怎么来评估数据的纯度,怎么来判断哪个属性对样本集的区别度最大呢。
信息熵 & 信息增益
信息熵: (information entropy)是度量样本集合纯度最常用的一种指标。假设一个样本集合 D D D,该样本集的信息熵的定义为:
E n t ( D ) = − ∑ k = 1 ∣ Y ∣ p k l o g 2 p k Ent(D) = - \sum_{k=1}^{|Y|}{p_klog_2p_k} Ent(D)=−k=1∑∣Y∣pklog2pk
其中:
p k p_k pk表示当前样本集中第 k k k类样本所占的比例。
从《机器学习实战》书中copy出计算python代码:
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): #iterate over all the features
featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
uniqueVals = set(featList) #get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): #compare this to the best gain so far
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i
return bestFeature
假设属性 a i a_i ai有 V V V种取值,那么对于属性 a i a_i ai的每种取值 V j V_j Vj,都会从样本集中衍生出一个新的样本集: D v D_v Dv。那么判断根据这个属性划分之后,那么就存在这么几个集合:
根节点的样本集: D D D, V个分支的V个样本集 D i , i ∈ 1... V D_i, i\in{1 ... V} Di,i∈1...V,可以根据上面的公式计算出V+1个信息熵出来。
如果属性集A总共有K个属性 a i , i ∈ 1... K a_i, i\in{1 ... K} ai,i∈1...K。总共就会有 K ( V + 1 ) K(V+1) K(V+1)个信息熵需要进行计算。
那么怎么判断哪个属性更好呢?需要根据 K ( V + 1 ) K(V+1) K(V+1)个信息熵来计算一个叫做信息增益的东西。
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a) = Ent(D) - \sum_{v=1}^{V}\frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
简单的来说,就是用根节点的信息熵,减去根据某个属性的某种划分生成的V个集合的信息熵之和。考虑到不同的分支节点所包含的样本数不同,给分支节点赋予权重 ∣ D v ∣ / ∣ D ∣ |D^v|/|D| ∣Dv∣/∣D∣,即样本数越多的分支节点的影响越大。
然后,再在K个属性中,每个属性计算一次信息增益,结果是哪个大,就选哪个作为划分属性。一旦把某个属性作为了划分属性,从属性集A中删除。
划分完第一个属性后,由于 D v D_v Dv替代了之前的 D D D成为了最新的 D D D,所以再需要根据剩下的 A − a i A-a_i A−ai个属性重新进行信息增益的计算。一直递归完成A属性集中所有属性的计算。
基尼指数
保持上面的计算过程不变,将计算信息增益的部分换一下,换成:
G i n i ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ≠ k ′ p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 Gini(D) = \sum_{k=1}^{|Y|}\sum_{k\neq k\prime}{p_kp_{k\prime}} \\ = 1 - \sum_{k=1}^{|Y|}{p_k^2} Gini(D)=k=1∑∣Y∣k=k′∑pkpk′=1−k=1∑∣Y∣pk2
也就是用基尼指数去描述一个数据样本集的“纯净”程度。这个公式可以描述为,挑选出同样两个不同类别的样本的概率,如果这个概率越高,说明样本集中不同类别的样本较多,就比较的不纯净。我们需要找到基尼指数最小的样本。
和信息熵一样,需要计算根据某种属性划分后,V个分支的基尼指数之和,和越小的就越好。
参考上述的公式:
G i n i i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini_index(D,a) = \sum_{v=1}^V{\frac{|D^v|}{|D|}Gini(D^v)} Giniindex(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
根据上一小节代码改造:
def calcGiniEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
GiniEnt += 1 - prob * prob
return shannonEnt
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): #iterate over all the features
featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
uniqueVals = set(featList) #get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcGiniEnt(subDataSet)
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): #compare this to the best gain so far
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i
return bestFeature
剪枝
决策树算法解决过拟合的方案是剪枝,也就是将从某个属性划分的节点出发的某个分支删掉。删掉分支有两个方法:
- 预剪枝。也就是在构建决策树的过程中,如果发现这条分支不需要,直接就不继续构建了。
- 后剪枝、也就是将决策树构建完成后,从根节点出发,从下往上搜索,如果发现从某条分支网上达到某个节点不需要,就进行删除。
怎么判断不需要呢?我们的判断标准是,增加一条分支,必须是增加这颗决策树的泛化能力。泛化能力如何叫做提升了呢?答案是使用测试集进行测试,如果增加分支后,测试集的准确率提升了,那就是泛化能力提升了。
预剪枝
预剪枝的话,就是在对每个属性的每个分支进行扩展的时候,判断一下这个分支增加之后,是否会使得测试集的准确率提高。
在递归构造树时增加测试集:
testVec = {XXXX}
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]#stop splitting when all of the classes are equal
if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
acc = testByVec(myTree, testVec);
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
acc_new = testByVec(myTree, testVec);
if(acc_new <= acc):
acc_new.del(myTree[bestFeatLable][value])
return myTree
后剪枝
后剪枝的话,可以先根据所有的叶子节点往上溯源,只要是剪枝后泛化能力还提升了的,那就执行。
上述的代码中的数据结构不适合用作后剪枝,我懒得专门写代码了,写一个伪代码算了:
leafs = tree.leafs;
for leaf in leafs[n]:
acc = testByVec(myTree, testVec)
newTree = tree.del(leaf)
acc_new = testByVec(newTree , testVec)
if(acc < acc_new):
tree = newTree
//把删除的叶子节点的父节点增加到检查节点中,后续继续判断
leafs.add(leaf.parent)
连续值 & 属性缺失处理
连续值
连续值的处理思路就是将连续值转换成离散值。
- 将样本中的所有连续值取值挑出来,并进行排序,获得数组: a 1 , a 2 . . . a n {a_1, a_2... a_n} a1,a2...an。
- 取每个取值的中间值作为划分点 t t t,就会有 n − 1 n-1 n−1个划分点: t 1 = ( a 1 + a 2 ) / 2 t_1 = (a_1+a_2)/2 t1=(a1+a2)/2,依次类推。
- 确定好划分点后,每个划分点可以将样本划分成两个子集合: D + , D − D^+, D^- D+,D−。相当于多了 n − 1 n-1 n−1个二值属性。
- 针对这 n − 1 n-1 n−1个二值属性,根据上面的信息增益或者基尼指数的计算方法来进行计算,可以获得最好的划分点。这个划分点就是该属性划分方法。
属性缺失
属性缺失的话,整体的思路就是通过给每一个样本给出权重,如果某个属性的某种取值缺失的比较多,而这些样本的权重又比较高的话,这些缺失与权重就会体现在信息增益公式中。
- ω x \omega_x ωx表示样本 x x x的权重
- D ~ \tilde{D} D~表示样本中某个属性没有缺失的样本集合。
- D k ^ \hat{D_k} Dk^表示样本中某个属性没有缺失的、类别为 k k k的样本集合。
- D v ~ \tilde{D^v} Dv~表示样本中某个属性没有缺失的、属性值等于 a v a_v av的样本集合。
根据这三个东西,再定义三个比例:
- ρ = ∑ x ∈ D ~ ω x ∑ x ∈ D ω x \rho = \frac{\sum_{x\in \tilde{D}}\omega_x}{\sum_{x\in D}\omega_x} ρ=∑x∈Dωx∑x∈D~ωx, 这个定义了在总样本中,没有缺失这个属性的样本的权重。
- p k ~ = ∑ x ∈ D k ~ ω x ∑ x ∈ D ~ ω x \tilde{p_k} = \frac{\sum_{x\in \tilde{D_k}}\omega_x}{\sum_{x\in \tilde{D}}\omega_x} pk~=∑x∈D~ωx∑x∈Dk~ωx, 这个定义了在没有缺失属性样本中,类别为 k k k的样本的权重。
- r v ~ = ∑ x ∈ D v ~ ω x ∑ x ∈ D ~ ω x \tilde{r_v} = \frac{\sum_{x\in \tilde{D^v}}\omega_x}{\sum_{x\in \tilde{D}}\omega_x} rv~=∑x∈D~ωx∑x∈Dv~ωx,这个定义了再没有缺失的属性样本中,属性取值为 a v a_v av的样本的权重。
根据这几个定义,把信息增益的计算方法改成:
G a i n ( D , a ) = ρ ∗ ( E n t ( D ~ ) − ∑ v = 1 V r v ~ E n t ( D v ~ ) ) Gain(D,a) = \rho * (Ent(\tilde{D}) - \sum_{v=1}^{V}\tilde{r_v}Ent(\tilde{D^v})) Gain(D,a)=ρ∗(Ent(D~)−v=1∑Vrv~Ent(Dv~))
其中:
E n t ( D ~ ) = − ∑ k = 1 ∣ Y ∣ p k ~ l o g 2 p k ~ Ent(\tilde{D}) = - \sum_{k=1}^{|Y|}{\tilde{p_k}log_2\tilde{p_k}} Ent(D~)=−k=1∑∣Y∣pk~log2pk~
也就是在计算信息增益之前,先统计一把缺失样本的权重,这里的 ω x \omega_x ωx就是需要琢磨的一个东西了。当然,我们可以把权重全部置为1。
多变量决策树
我理解的多变量决策树就是将每个划分节点综合多个节点。
上面讲的所有的属性划分都是针对单个的属性,而有些情况下,根据一个属性并不能将一些样本做很好的线性划分,导致树的深度太大,从而导致计算量增加。而综合多个变量,让多个变量组成相应的线性关系,就能更好的进行分类。
比如将书中提到的“密度”和“含糖率”做一个线性组合:
w = a ∗ 密 度 + b ∗ 含 糖 率 w = a * 密度+b * 含糖率 w=a∗密度+b∗含糖率
然后将 w w w作为一个组合属性就行划分。
