图的存储结构（邻接矩阵、邻接表、十字链表）

目录

一、相关概念

二、图的存储结构

2.1 邻接矩阵表示法

2.1.1 邻接矩阵存储的基本思想

2.1.2 存储结构的定义

2.1.3 用邻接矩阵表示法创建带权有向图

2.1.4 销毁邻接矩阵 

2.2 邻接表表示法

2.2.1 邻接表存储的基本思想

2.2.2 存储结构的定义

2.2.3 用邻接表表示法创建带权有向图

2.2.4 销毁邻接表

2.3 十字链表表示法

2.3.1 十字链表存储的基本思想

​2.3.2 存储结构的定义 

2.3.3 用十字链表表示法创建带权有向图 

2.3.4 销毁十字链表

---

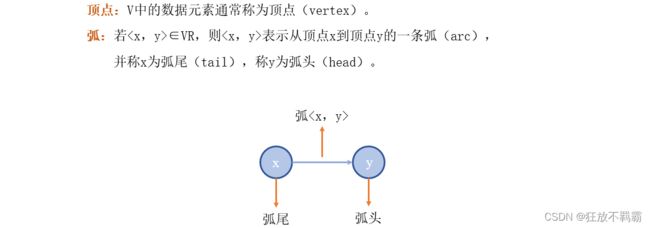
一、相关概念

图是一种网状数据结构。

---

二、图的存储结构

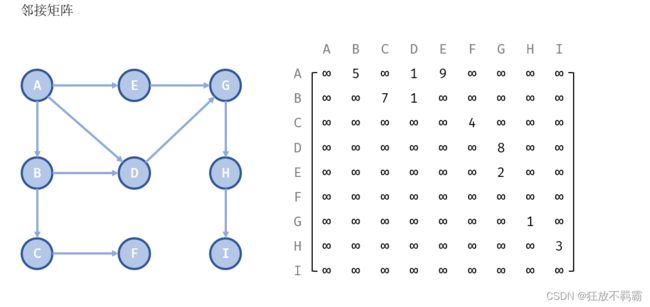
2.1 邻接矩阵表示法

2.1.1 邻接矩阵存储的基本思想

图的邻接矩阵表示法，又称数组表示法。它采用两个数组来表示图：

1、用于存储顶点信息的一维数组；

2、用于存储图中顶点之间关联关系的二维数组，称为邻接矩阵。

无权图的邻接矩阵：

带权图的邻接矩阵： 

2.1.2 存储结构的定义

图的种类：

DG —— 有向图、DN —— 有向网、UDG ——无向图、UDN —— 无向网

#define MAX_VERTEX_NUM 20 /* 最多顶点个数 */
#define INFINITY 32768 /* 代表无穷大 */

typedef enum{DG, DN, UDG, UDN} GraphKind; /* 图的种类 */
typedef char VertexData;

/* 定义弧的类型 */
typedef struct ArcNode {
    AdjType adjvex;
    OtherInfo info;
} ArcNode;

/* 定义顶点的类型 */
typedef struct VertexNode {
    VertexData data; //顶点数据，一般为字符标签
} VertexNode;

/* 邻接矩阵表示法 */
typedef struct Graph {
    VertexNode vertex[MAX_VERTEX_NUM];               /* 顶点向量 */
    ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];    /* 邻接矩阵 */
    int vexnum, arcnum;                              /* 图的顶点数和弧数 */
    GraphKind kind;                                  /* 图的种类标志 */
} AdjMatrix, Graph;

2.1.3 用邻接矩阵表示法创建带权有向图

void CreateGraph(Graph *G) {
    int i, j, k, weight;
    int kind;
    VertexData v1, v2;

    scanf("%d,%d,%d", &kind, &G->vexnum, &G->arcnum);
    getchar(); /* 吸收掉换行符 */

    G->kind = kind;

    /* 初始化邻接矩阵 */
    for (i = 0; i < G->vexnum; i++)
        for (j = 0; j < G->vexnum; j++)
            G->arcs[i][j].adjvex = INFINITY;

    /* 存储顶点信息 */
    for (i = 0; i < G->vexnum; i++) {
        scanf("%c", &G->vertex[i].data);
    }
    getchar();

    /* 创建邻接矩阵 */
    for (k = 0; k < G->arcnum; k++) {
        /* 读入一条弧的两个顶点及权值 */
        scanf("%c,%c,%d", &v1, &v2, &weight);
        getchar();

        /* 查找顶点在顶点向量里的位序 */
        i = LocateVertex(G, v1);
        j = LocateVertex(G, v2);

        /* 写入权值，建立弧 */
        G->arcs[i][j].adjvex = weight;
    }
}

2.1.4 销毁邻接矩阵 

void DestroyGraph(Graph *G) {
    G->vexnum = G->arcnum = 0;
    G->kind = UNDEFINED;
}

---

2.2 邻接表表示法

2.2.1 邻接表存储的基本思想

邻接表表示法是图的一种链式存储结构，基本思想是只存储图中存在的边的信息。

在邻接表中，对图的每个顶点建立一个带头结点的边表，每个边表的头结点又构成一个表头结点表。

表头结点表和边表： 

示意图：

2.2.2 存储结构的定义

#define MAX_VERTEX_NUM 20 /* 最多顶点个数 */
typedef enum{DG, DN, UDG, UDN} GraphKind; /* 图的种类 */

/* 定义表头结点的类型 */
typedef struct VertexNode {
    VertexData data;    //数据域，存放顶点信息
    ArcNode * firstarc; //指针域，指向边表中第一个结点
} VertexNode;

/* 定义边结点的类型 */
typedef struct ArcNode {
    AdjType adjvex;           //邻接点域，边的终点在顶点表中的下标
    OtherInfo info;           //数据域，存放其它相关信息
    struct ArcNode * nextarc; //指针域，指向边表中的下一个结点
} ArcNode;

2.2.3 用邻接表表示法创建带权有向图

void CreateGraph(Graph *G) {
    int i, j, k;
    int kind, w;
    ArcNode * arc;
    VertexData v1, v2;

    scanf("%d,%d,%d", &kind, &G->vexnum, &G->arcnum);
    getchar();

    G->kind = kind;

    for (i = 0; i < G->vexnum; ++i) {
        scanf("%c", &G->vertex[i].data);
        /* 将边表置为空 */
        G->vertex[i].firstarc = NULL;
    }
    getchar();

    /* 添加边i--->j */
    for (k = 0; k < G->arcnum; ++k) {
        /* 输入顶点信息和边的权值 */
        scanf("%c,%c,%d", &v1, &v2, &w);
        getchar();

        i = LocateVertex(G, v1); /* v1顶点在顶点数组中的下标值 */
        j = LocateVertex(G, v2); /* v2顶点在顶点数组中的下标值 */

        /* 生成新的边结点 */
        arc = (ArcNode *)malloc(sizeof(ArcNode));
        arc->adjvex = j;
        arc->info.weight = w;

        /* 通过头插法插入边表中，成为新的firstarc */
        arc->nextarc = G->vertex[i].firstarc;
        G->vertex[i].firstarc = arc;
    }
}

2.2.4 销毁邻接表

void DestroyGraph(Graph *G) {
    ArcNode * p, * q;

    for (int i = 0; i < G->vexnum; ++i) {
        p = G->vertex[i].firstarc;
        /* 释放所有的边界点 */
        while (p != NULL) { /* p在前，q在后 */
            q = p;
            p = p->nextarc;
            free(q);
        }
    }

    G->arcnum = G->vexnum = 0;
    G->kind = UNDEFINED;
}

 

---

2.3 十字链表表示法

2.3.1 十字链表存储的基本思想

十字链表可以看成是将有向图的邻接表和逆邻接表结合起来的一种链表。

有向图中的每一个顶点在十字链表中对应有一个结点，称为顶点结点；

有向图中的每一条弧在十字链表中对应有一个结点，称为弧结点。

示意图： 

 

2.3.2 存储结构的定义 

#define MAX_VERTEX_NUM 20 /* 最多顶点个数 */
typedef enum{DG, DN, UDG, UDN} GraphKind; /* 图的种类 */

/* 定义顶点结点 */
typedef struct VertexNode {
    VertexData data;
    ArcNode *firstin, *firstout;
} VertexNode;

/* 定义弧结点 */
typedef struct ArcNode {
    int tailvex, headvex;
    struct ArcNode *hlink, *tlink;
    OtherInfo info;
} ArcNode;

/* 十字链表表示法 */
typedef struct Graph {
    VertexNode vertex[MAX_VERTEX_NUM];
    int vexnum, arcnum; /*图的顶点数和弧数*/
    GraphKind kind;     /*图的种类*/
} OrthList, Graph;

2.3.3 用十字链表表示法创建带权有向图 

void CreateGraph(Graph *G) {
    int n, e;
    int i, j, k;
    int kind, w;
    char vt, vh;
    ArcNode *p;

    scanf("%d,%d,%d", &kind, &n, &e);
    getchar();
    G->vexnum = n;
    G->arcnum = e;
    G->kind = DN;

    /* 生成顶点结点 */
    for (i = 0; i < n; i++) {
        scanf("%c", &G->vertex[i].data);
        G->vertex[i].firstin = NULL;
        G->vertex[i].firstout = NULL;
    }
    getchar();

    /* 生成弧结点 */
    for (k = 0; k < e; k++) {
        scanf("%c,%c,%d", &vt, &vh, &w);
        getchar();
        i = LocateVertex(G, vt);
        j = LocateVertex(G, vh);
        p = (ArcNode *)malloc(sizeof(ArcNode));
        p->info.weight = w;
        p->tailvex = i;
        p->headvex = j;
        /* 头插法 */
        p->tlink = G->vertex[i].firstout;
        G->vertex[i].firstout = p;
        p->hlink = G->vertex[j].firstin;
        G->vertex[j].firstin = p;
    }
}

2.3.4 销毁十字链表

邻接表中的所有弧结点被释放掉了，自然逆邻接表中的所有弧结点也被释放掉了。

void DestroyGraph(Graph *G) {
    ArcNode *p, *q;

    for (int i = 0; i < G->vexnum; i++) {
        p = G->vertex[i].firstout;
        while (p != NULL) {
            q = p;
            p = p->tlink;
            free(q);
        }
    }
}