计算机视觉入门学习笔记(二)——图像预处理
原视频教程:
https://www.bilibili.com/video/BV19x411X7k6?from=search&seid=9816644268076164289
一、图像显示与储存原理
1.1、图像怎么显示
计算机视觉中,主要有RGB颜色空间与HSV颜色空间:
RGB:三个颜色通道(RGB),有时候有四个(ARGB)
HSV:三个通道(HSV),色调、饱和度、亮度
1.2、图像怎么储存
二、图像增强的目标
改善视觉效果,转为更适合人或者机器分析,突出有意义的东西,抑制无用信息
空间域处理:点运算【直方图】,形态学运算【膨胀,腐蚀】,临域运算【卷积,金字塔】
频率域处理:傅里叶变换,小波变换
三、点运算:基于直方图的对比度增强
3.1 直方图是什么
将某一张照片的像素灰度[0,255]全部找出来,并按照个数统计其分布,得到的统计曲线就是直方图,如下图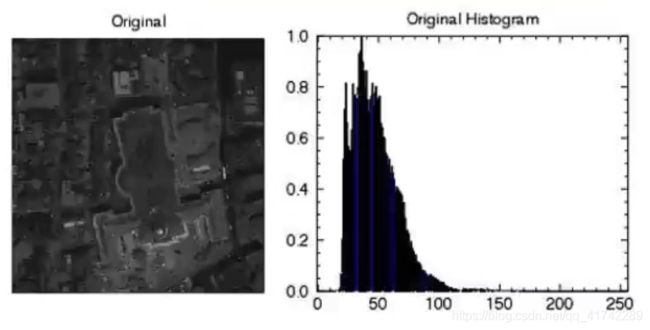
3.2 直方图均衡化(经典方法)
如3.1图,可以看出此时灰度分布不均匀,图像集中在了较暗的地方。这种情况大多数是因为相机的的成像、曝光等等有问题,可以通过直方图均衡化来调整。对直方图进行非线性拉伸,使得其大致均匀分布。注意通常为非线性拉伸。

3.3 自适应直方图均衡化(AHE)
简单地非线性拉伸直方图成为直方图均衡化的经典算法,想象一下,当图像中存在过亮的情况,比如正对着光源拍摄,这种情况使用经典算法,会导致亮的部分更亮,因此经典算法作用有限,可以使用自适应直方图均衡化。分为以下几步:
1、设定一个模板,在原始图片上滑动,步长固定;
2、在滑动的时候,对模板覆盖住的区域进行直方图均衡的经典算法,并对每个像素点进行结果赋值;
3、滑动结束后 ,每个像素点会有多个赋值,取多个赋值的均值为最终的结果,这个结果成为即为AHE得到的映射函数。
3.4 限制对比度自适应直方图均衡(CLAHE) 没搞懂
AHE有一个缺点,他在处理的时候,会将图片噪声放大,因此提出了CLAHE。大致过程为,在AHE的基础之上,把左图中超出阈值的部分整体拆分移动到底部,使得整个直方图抬高。
简单地进行上述移动还会带来图片不连续的问题,如相邻两个像素点差距过大,但是我不知道为什么。为了解决这个问题, 需要对AHE得到的映射函数稍微加工一下,如下图2.
四、形态学处理
膨胀与腐蚀
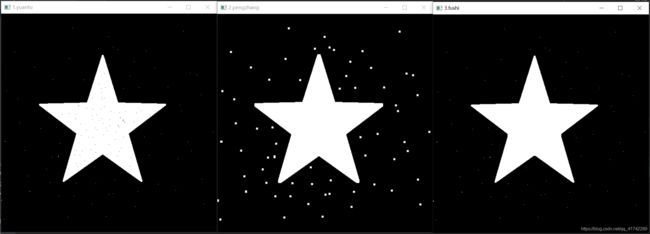
开运算:先腐蚀再膨胀,可以去掉目标外的孤立点
闭运算:先膨胀再腐蚀,可以去掉目标内的孔
开运算中:腐蚀后,五角星外的白点会被腐蚀消失,同时五角星会往外扩张一小圈;再膨胀的时候,五角星会缩回原先的样子,而白点已经消失了。

闭运算中:膨胀后,五角星内的黑点会因为边缘的白色向其膨胀而消失;再腐蚀使得五角星和外部的白点恢复原样,而黑点已经消失了。
五、空间域处理:卷积
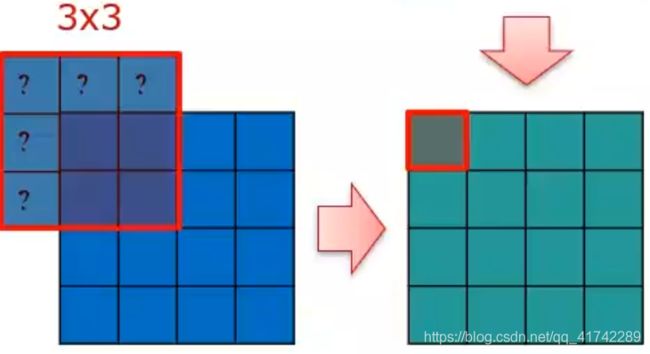
卷积的时候如果不进行边界扩充(Padding),那么卷积结果一定是比原来的图片要小。如图,用3 * 3的卷积核对4 * 4大小的图片进行卷积,当不进行边界扩充时候, 需要把卷积核边缘同图片边缘对齐,得到的结果必定比原图片小。

当进行边界扩充时候,将卷积核中心与目标位置对齐,超出图片的部分假定为某个值,使得卷积后的大小与原图片保持一致。
边界填充策略一般有:0,边界值,镜像,块复制。补0用得最多,但在使用的时候需要避免大卷积核与小图片的搭配——这样在卷积的时候,边界有很多本没有的0加入运算,而中心位置没有额外加入的0,导致中间和边界的数值差距变大,会造成较大误差。
当卷积核是对称的时候,可以将卷积核拆解成 列*行 级联的形式,然后对图片先进行列卷积,再进行行卷积,得到的结果和直接卷积的结果是一样的。这样拆解的好处是降低了卷积运算的复杂度,由N2降为了2N(这里也没搞懂)。等我写出来代码应该就能看出来复杂度的变化了。
魔鬼细节:卷积运算本身并不是矩阵相乘,而是对应位置直接相乘相加;而有时候,我们会把卷积核倒转一下,或者设定对称的卷积核,使其变成矩阵相乘。
六、卷积的应用(平滑、边缘检测、锐化)
1、平滑
以3*3的卷积核为例,每个位置相乘后应得到9个值,卷积是对这9个位置直接相加,滤波其实是根据这9个值,采用某种方法来计算结果。
| 滤波方法 | 卷积核 | 过程 | 评价 |
|---|---|---|---|
| 均值滤波 | 卷积核值全为1 | 对9个值取均值,作为该位置的结果 | 平均值会降低像素间区分度,不能很好地去噪,还破坏了细节 |
| 中值滤波 | 卷积核值全为1 | 对9个值取中值,作为该位置的结果 | 很好地去噪 |
| 高斯滤波 | 卷积核中心值大,边缘小,所有值相加为1 | 对9个值相加,作为该位置的结果 | 把图片变模糊 |
高斯滤波的有一个参数δ,这个参数代表了卷积核
看起来似乎没什么用,把图片变模糊算什么本事?在8.1中会有叙述。
2、边缘检测
| 滤波方法 | 卷积核 | 过程 | 评价 |
|---|---|---|---|
| 水平梯度滤波 | (-1,0,1) (-1,0,1) (-1,0,1) |
相乘相加 | 放大垂直边缘差异,检测垂直边缘 |
| 垂直梯度滤波 | (-1,-1,-1) ( 0, 0, 0) ( 1, 1, 1) |
相乘相加 | 放大水平边缘差异,检测水平边缘 |
| Sobel 梯度滤波 | (-1,-2,-1) ( 0, 0, 0) ( 1, 2, 1) |
相乘相加 | 基础梯度滤波的改进版 |
| Laplacian 梯度滤波 | 中间大,四周小,相加等于0,如 ( 0, 1, 0) ( 1,-4, 1) ( 0, 1, 0) |
相乘相加 | 检测变化明显的地方,并且过滤平滑,用于细节锐化 |
3、锐化
Laplacian 梯度滤波示例

边上黑色的区域十分平滑,基本保持某个灰度不变。在和为0的卷积核作用下,会变成0,达到了过滤平滑的效果。环形山部分尤其是环形山边缘变化较明显,在中心大的卷积核作用下,会凸显出来。(第二张图的效果)
将卷积后的结果与原图相加,平滑部分值为0不变,细节部分更加明显,达到锐化效果。
七、频率域处理:傅里叶变换,小波变换
1、如何让卷积更快
空间域卷积 = 频率域乘积(看不懂)
2、傅里叶变换
傅里叶变换是什么就不赘述, 公式也推导我也看不懂,但结论是可以理解的:一个信号可以拆成若干个正弦信号和余弦信号的总和。
可这是信号啊,图像处理跟信号有什么关系?其实一目了然,下面给出两个简单的图像进行傅里叶变换的结果。上方的两张原图都是有强烈的频率特征的,经过傅里叶变换后就得到了下方简单的三个点。

傅里叶变换的不足:
无法应对变频信号和突变信号。
改进:
STFT(短时傅里叶变换),把时间轴分块,在每一块中认为信号是平稳的,不突变的。缺点是分块大小不好掌握。
3、小波变换
小波变换的公式就算了,我看不懂。
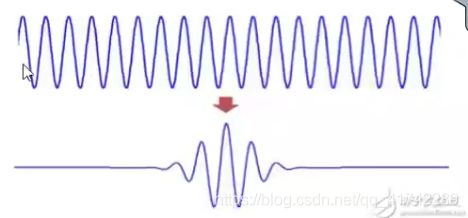
基于STFT再次改进就成了小波变换(但是我怎么觉得这两个完全不同呢?),按照原先的傅里叶变换方法,一个信号会被拆成若干个正弦波和余弦波的总和,这些拆出来的波都是在时间域上无限长的(如上面的波形)
小波变换就是把这些波改成逐渐衰减的波形(小一点的波),经过一定时间后会趋近于0。
八、应用案例
1、高斯金字塔
在应用中,经常会遇到需要缩放图片的情况,举个例子:
将 128 * 128 的图片缩放成 64 * 64,即长宽为 2 * 2 的每四个像素需要合并为一个新的像素。那么新的像素应该选用原先四个像素中的哪一个呢?或者说应该用什么方式来计算得出新的像素?
1、先对这四个像素进行高斯滤波,使得四个像素更加平滑;
2、之后可以任取一个像素点作为新像素,也可以取这四个像素的平均值;
3、重复这个降采样过程,得到的就是高斯金字塔。

高斯金字塔除了用于缩放图片,还有很多其他的用处。例如在目标检测算法中,待检测的目标可能很大,也可能很小,对于同一个算法来说,就需要用到高斯金字塔来进行逐步降采样。(还没搞懂)
2、拉普拉斯字塔
这个东西看起来很高级,我尽量用自己语言来组织。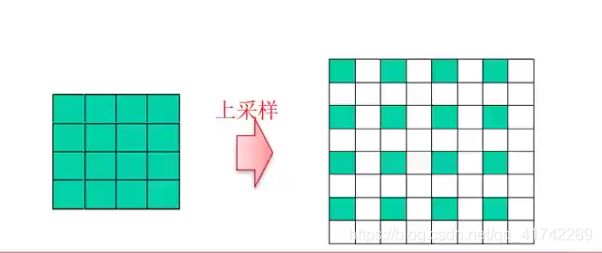
如图,对已经进行高斯滤波并降采样的某个图片重新放大,扩充的像素直接使用同样的数值填充,得到的图片与原图的差值,就是拉普拉斯金字塔。
下面这个图看起来很高级,且看我慢慢道来。
首先看左侧一列,这是前文中提到的高斯金字塔下采样的过程,这很好理解。
之后看中间的一列,将第一次高斯滤波下采样得到的图片重新放大,扩充的像素直接使用同样的数值填充,得到的图片与原始图片的差值,作为拉普拉斯金字塔的第一层;同理,将第二次下采样的图片重新填充放大后与第一次下采样图片的差值,作为拉普拉斯金字塔的第二层;
有了高斯金字塔和拉普拉斯金字塔,就能够精准恢复原先的图片了,这是简单的加减法问题,很好理解。
3、傅里叶变换
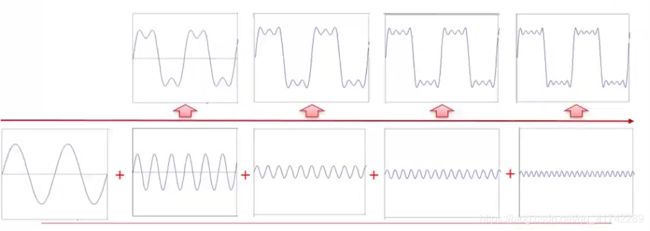
先看这个图,对于一个信号的傅里叶变换来说,越高频的波,其幅值越小,反应到合成图像上,表达的信息就越细小。因此高频信号表示原信号的细节,低频信号表示原信号主体部分。
同理,对于图像傅里叶变换后的图像而言:
越靠近中心的点,它表示的频率越低,反应到原图像上就是越主要的部分。低频代表主体。
越远离中心的点,它表示的频率越高,反应到原图像上就是更细节的部分。高频代表细节。
由此,可以得到新的滤波方法:
低通滤波:若去除FFT边缘部分,保留中心,其实是去除了高频,保留了低频区域,即去除了细节,保留了图片主体。
高通滤波:若去除FFT中心部分,保留边缘,其实是去除了低频,保留了高频区域,即去除了主体,保留了图片细节。

频段滤除:有个老旧的黑白电视机,工作的时候会有黑白条纹遮挡。将其进行傅里叶变换,得到的图像上面,条纹其实是两个点。把这两个点去掉,再恢复到原图,就可以去掉这个黑白条纹了。