【监督学习】多层感知器MLP(含代码实现)
大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流
个人主页-Sonhhxg_柒的博客_CSDN博客
欢迎各位→点赞 + 收藏⭐️ + 留言
系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟
1、多层感知器MLP
感知器(Perceptron)是ANN人工神经网络(请参见人工智能(25))的一个概念,由Frank Rosenblatt于1950s第一次引入。
单层感知器(Single Layer Perceptron)是最简单的ANN人工神经网络。它包含输入层和输出层,而输入层和输出层是直接相连的。单层感知器仅能处理线性问题,不能处理非线性问题。今天想要跟大家探讨的是MLP多层感知器。
MLP多层感知器是一种前向结构的ANN人工神经网络, 多层感知器(MLP)能够处理非线性可分离的问题。
MLP概念:
MLP多层感知器(Multi-layerPerceptron)是一种前向结构的人工神经网络ANN,映射一组输入向量到一组输出向量。MLP可以被看做是一个有向图,由多个节点层组成,每一层全连接到下一层。除了输入节点,每个节点都是一个带有非线性激活函数的神经元。使用BP反向传播算法的监督学习方法来训练MLP。MLP是感知器的推广,克服了感知器不能对线性不可分数据进行识别的弱点。
相对于单层感知器,MLP多层感知器输出端从一个变到了多个;输入端和输出端之间也不光只有一层,现在又两层:输出层和隐藏层。
基于反向传播学习的是典型的前馈网络, 其信息处理方向从输入层到各隐层再到输出层,逐层进行。隐层实现对输入空间的非线性映射,输出层实现线性分类,非线性映射方式和线性判别函数可以同时学习。
MLP激活函数
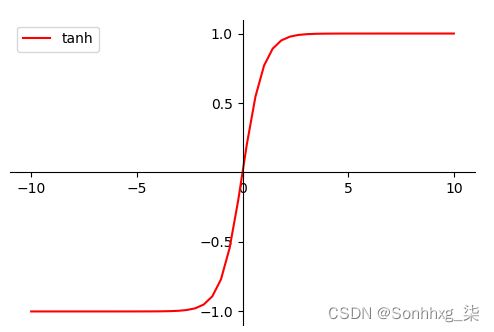
MLP可使用任何形式的激活函数,譬如阶梯函数或逻辑乙形函数(logistic sigmoid function),但为了使用反向传播算法进行有效学习,激活函数必须限制为可微函数。由于具有良好可微性,很多乙形函数,尤其是双曲正切函数(Hyperbolictangent)及逻辑乙形函数,被采用为激活函数。
激活函数的作用是将非线性引入神经元的输出。因为大多数现实世界的数据都是非线性的,希望神经元能够学习非线性的函数表示,所以这种应用至关重要。
MLP原理:
前馈神经网络是最先发明也是最简单的人工神经网络。它包含了安排在多个层中的多个神经元。相邻层的节点有连接或者边(edge)。所有的连接都配有权重。
一个前馈神经网络可以包含三种节点:
1)输入节点(Input Nodes):也称为输入层,输入节点从外部世界提供信息,。在输入节点中,不进行任何的计算,仅向隐藏节点传递信息。
2)隐藏节点(Hidden Nodes):隐藏节点和外部世界没有直接联系。这些节点进行计算,并将信息从输入节点传递到输出节点。隐藏节点也称为隐藏层。尽管一个前馈神经网络只有一个输入层和一个输出层,但网络里可以没有也可以有多个隐藏层。
3)输出节点(Output Nodes):输出节点也称为输出层,负责计算,并从网络向外部世界传递信息。
在前馈网络中,信息只单向移动——从输入层开始前向移动,然后通过隐藏层,再到输出层。在网络中没有循环或回路。
MLP多层感知器就是前馈神经网络的一个例子,除了一个输入层和一个输出层以外,至少包含有一个隐藏层。单层感知器只能学习线性函数,而多层感知器也可以学习非线性函数。
MLP训练过程:
一般采用BP反向传播算法来训练MPL多层感知器。采用BP反向传播算法就像从错误中学习。监督者在人工神经网络犯错误时进行纠正。MLP包含多层节点;输入层,中间隐藏层和输出层。相邻层节点的连接都有配有权重。学习的目的是为这些边缘分配正确的权重。通过输入向量,这些权重可以决定输出向量。在监督学习中,训练集是已标注的。这意味着对于一些给定的输入,能够知道期望的输出(标注)。
MLP训练过程大致如下:
1)所有边的权重随机分配;
2)前向传播:利用训练集中所有样本的输入特征,作为输入层,对于所有训练数据集中的输入,人工神经网络都被激活,然后经过前向传播,得到输出值。
3)反向传播:利用输出值和样本值计算总误差,再利用反向传播来更新权重。
4)重复2)~3), 直到输出误差低于制定的标准。
上述过程结束后,就得到了一个学习过的MLP网络,该网络被认为是可以接受新输入的。
MLP优点:
1)高度的并行处理;
2)高度的非线性全局作用;
3)良好的容错性;
4)具有联想记忆功能;
5)非常强的自适应、自学习功能。
MLP缺点:
1)网络的隐含节点个数选取非常难;
2)停止阈值、学习率、动量常数需要采用”trial-and-error”法,极其耗时;
3)学习速度慢;
4)容易陷入局部极值;
5)学习可能会不够充分。
MLP应用:
MLP在80年代的时候曾是相当流行的机器学习方法,拥有广泛的应用场景,譬如语音识别、图像识别、机器翻译等等,但自90年代以来,MLP遇到来自更为简单的支持向量机的强劲竞争。近来,由于深层学习的成功,MLP又重新得到了关注。
常被MLP用来进行学习的反向传播算法,在模式识别的领域中算是标准监督学习算法,并在计算神经学及并行分布式处理领域中,持续成为被研究的课题。MLP已被证明是一种通用的函数近似方法,可以被用来拟合复杂的函数,或解决分类问题。
2、MLP的代码实现
from __future__ import print_function, division
import numpy as np
import math
from sklearn import datasets
from mlfromscratch.utils import train_test_split, to_categorical, normalize, accuracy_score, Plot
from mlfromscratch.deep_learning.activation_functions import Sigmoid, Softmax
from mlfromscratch.deep_learning.loss_functions import CrossEntropy
class MultilayerPerceptron():
"""Multilayer Perceptron classifier. A fully-connected neural network with one hidden layer.
Unrolled to display the whole forward and backward pass.
Parameters:
-----------
n_hidden: int:
The number of processing nodes (neurons) in the hidden layer.
n_iterations: float
The number of training iterations the algorithm will tune the weights for.
learning_rate: float
The step length that will be used when updating the weights.
"""
def __init__(self, n_hidden, n_iterations=3000, learning_rate=0.01):
self.n_hidden = n_hidden
self.n_iterations = n_iterations
self.learning_rate = learning_rate
self.hidden_activation = Sigmoid()
self.output_activation = Softmax()
self.loss = CrossEntropy()
def _initialize_weights(self, X, y):
n_samples, n_features = X.shape
_, n_outputs = y.shape
# Hidden layer
limit = 1 / math.sqrt(n_features)
self.W = np.random.uniform(-limit, limit, (n_features, self.n_hidden))
self.w0 = np.zeros((1, self.n_hidden))
# Output layer
limit = 1 / math.sqrt(self.n_hidden)
self.V = np.random.uniform(-limit, limit, (self.n_hidden, n_outputs))
self.v0 = np.zeros((1, n_outputs))
def fit(self, X, y):
self._initialize_weights(X, y)
for i in range(self.n_iterations):
# ..............
# Forward Pass
# ..............
# HIDDEN LAYER
hidden_input = X.dot(self.W) + self.w0
hidden_output = self.hidden_activation(hidden_input)
# OUTPUT LAYER
output_layer_input = hidden_output.dot(self.V) + self.v0
y_pred = self.output_activation(output_layer_input)
# ...............
# Backward Pass
# ...............
# OUTPUT LAYER
# Grad. w.r.t input of output layer
grad_wrt_out_l_input = self.loss.gradient(y, y_pred) * self.output_activation.gradient(output_layer_input)
grad_v = hidden_output.T.dot(grad_wrt_out_l_input)
grad_v0 = np.sum(grad_wrt_out_l_input, axis=0, keepdims=True)
# HIDDEN LAYER
# Grad. w.r.t input of hidden layer
grad_wrt_hidden_l_input = grad_wrt_out_l_input.dot(self.V.T) * self.hidden_activation.gradient(hidden_input)
grad_w = X.T.dot(grad_wrt_hidden_l_input)
grad_w0 = np.sum(grad_wrt_hidden_l_input, axis=0, keepdims=True)
# Update weights (by gradient descent)
# Move against the gradient to minimize loss
self.V -= self.learning_rate * grad_v
self.v0 -= self.learning_rate * grad_v0
self.W -= self.learning_rate * grad_w
self.w0 -= self.learning_rate * grad_w0
# Use the trained model to predict labels of X
def predict(self, X):
# Forward pass:
hidden_input = X.dot(self.W) + self.w0
hidden_output = self.hidden_activation(hidden_input)
output_layer_input = hidden_output.dot(self.V) + self.v0
y_pred = self.output_activation(output_layer_input)
return y_pred
def main():
data = datasets.load_digits()
X = normalize(data.data)
y = data.target
# Convert the nominal y values to binary
y = to_categorical(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, seed=1)
# MLP
clf = MultilayerPerceptron(n_hidden=16,
n_iterations=1000,
learning_rate=0.01)
clf.fit(X_train, y_train)
y_pred = np.argmax(clf.predict(X_test), axis=1)
y_test = np.argmax(y_test, axis=1)
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy:", accuracy)
# Reduce dimension to two using PCA and plot the results
Plot().plot_in_2d(X_test, y_pred, title="Multilayer Perceptron", accuracy=accuracy, legend_labels=np.unique(y))
if __name__ == "__main__":
main()