【视觉预训练】《BEIT: BERT Pre-Training of Image Transformers》 ICLR 2022

《BEIT: BERT Pre-Training of Image Transformers》

回顾 VLMo

BERT 回顾

在BERT中，每个单词或者字会分配一个 token，所以模型的输入是一系列 token id。MLM训练方式是 mask 一个位置的token，然后经过BERT之后预测这个位置的 token是什么。由于mask 的位置是我们自己选的，所以我们是有预测任务的 Ground Truth的，因此可以来优化模型参数

BERT应用于视觉任务

BERT应用在视觉任务上最大的困难是：视觉任务没有一个大的词汇表（vocabulary），比如上图 mask “湾”，softmax 预测 “湾” 的token id就好了。但是在CV任务中，mask一块patch，预测的Ground Truth是什么呢？

其实也有Ground Truth，直接恢复原图像patch的pixel。但是这样像素级别的恢复任务的缺点是 把模型的建模能力浪费在了 short-range dependencies 和 high-frequency details

为了解决这个问题，本文提出的这个方法叫做 BEIT，很明显作者是想在 CV 领域做到和 NLP 领域的 BERT 一样的功能。训练好的 BERT 模型相当于是一个 Transformer 的 Encoder，它能够把一个输入的 sentence 进行编码，得到一堆 tokens。 BEIT 也是在做类似的事情，即能够把一个输入的 image 进行编码，得到一堆 vectors，并且这些个 vectors 也结合了 image 的上下文。

模型输入

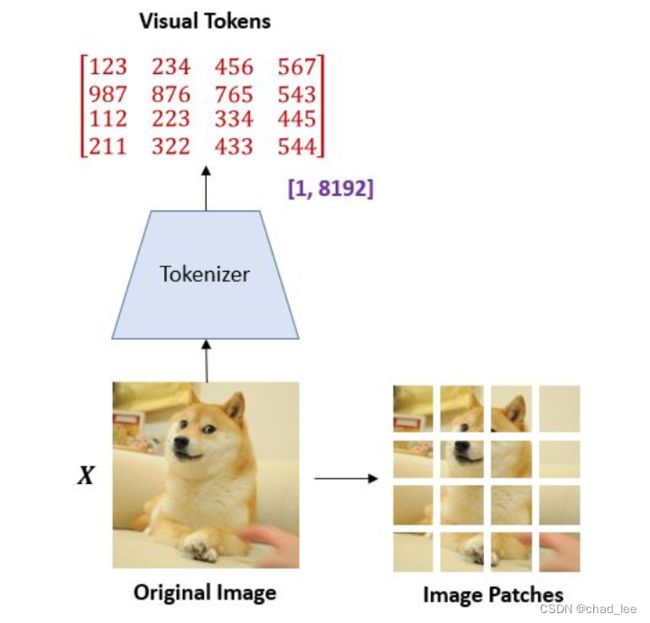
在 BEIT 眼里，图片有 2 种表示的形式，即可以看作 image patches，又可以看作 visual tokens，在预训练的过程中，它们分别被作为模型的输入和输出，如下图所示：

将图片表示为 image patches 这个操作和 Vision Transformer 对图片的处理手段是一致的。将 $x\in {\mathbb{R}}^{H\times W\times C}$ 的图片拉成 $x^p\in {\mathbb{R}}^{N\times \left(P^{2}C\right)}$ 的输入。

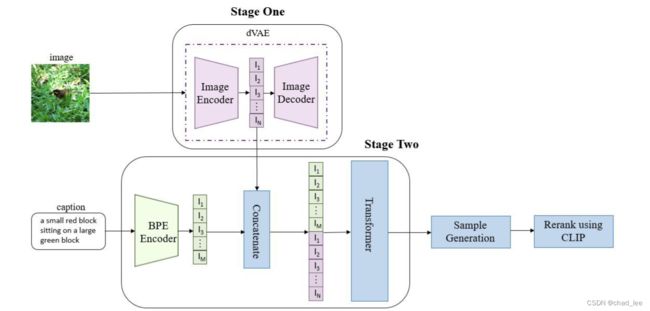
然后利用dVAE的 image tokenizer，把一张图片 $x\in {\mathbb{R}}^{H\times W\times C}$ 离散成 tokens $z=\left[z_1,\dots ,z_N\right]\in {\mathcal{V}}^{h\times w}$，字典 $\mathcal{V}=\{1,\dots ,|\mathcal{V}|\}$ 包含了所有离散索引。具体而言，作者训练了一个 discrete variational autoencoder (dVAE)，训练的过程如下：

所以一张 224×224 的输入图片通过 Tokenizer 变成了 14×14 个 visual token，每个 visual token 是一个位于[1,8192]之间的数。就像有个 image 的词汇表一样，这个词汇表里面有 8192 个词，每个 16×16 的image patch会经过 Tokenizer 映射成 |V| 里面的一个词。因为 visual token 是离散的数，所以优化时没法求导，所以采用了 gumbel softmax 技巧。

BEIT模型

BEIT 的总体结构如下，BEIT 的 Encoder 结构就是 Transformer 的 Encoder，模型架构是一样的。图片在被分成 $N=HW/P^2$ 个展平的2D块 $x^p\in {\mathbb{R}}^{N\times \left(P^{2}C\right)}$ 之后，通过线性变换得到 $\mathbf{E}{x}_i^p$，其中 $\mathbf{E}\in {\mathbb{R}}^{\left(P^{2}C\right)\times D}$ 。在concat上一个 special token [S]。这里作者还给输入加上了 1D 的位置编码 ${\mathbf{E}}_{pos}\in {\mathbb{R}}^{N\times D}$，所以总的输入张量可以表示为：
$${\mathbf{H}}_0=\left[{\mathbf{e}}_{[\mathrm{s}]},\mathbf{E}{x}_i^p,\dots ,\mathbf{E}{x}_N^p\right]+{\mathbf{E}}_{pos}$$

输入 BEIT 的 Encoder (就是 Transformer 的 Encoder) 之后，张量依次通过 L 个 Encoder Block：
$${\mathbf{H}}^l=\mathrm{Transformer}\left({\mathbf{H}}^{l-1}\right)$$
最后一层输出 ${\mathbf{H}}^L=\left[{\mathbf{h}}_{[s]}^L,{\mathbf{h}}_1^L,\dots ,{\mathbf{h}}_N^L\right]$ 作为 image patches 的 encoded representations。

训练方式

既然BEIT 是图像界的 BERT 模型，所以也遵循着和 BERT 相似的自监督训练方法。核心思想是：让 BEIT 看很多的图片，随机盖住一些 image patches，让 BEIT 模型预测盖住的patches是什么，不断计算预测的 patches 与真实的 patches 之间的差异，利用它作为 loss 进行反向传播更新参数，来达到 Self-Supervised Learning 的效果。

具体做法为：

1. 给定输入图片 $\mathbf{x}$。
2. 把 $\mathbf{x}$ 变成 N 个 image patches ${\left\{{\mathbf{x}}_i^p\right\}}_{i=1}^N$。
3. 把 $\mathbf{x}$ 变成 N 个 visual tokens ${\left\{z_i\right\}}_{i=1}^N$。
4. 随机盖住40% 的 image patches，盖住的位置可以表示为 $\mathcal{M}\in \{1,\dots ,N{\}}^{0.4N}$
5. 把盖住的这40%的image patches 替换成可学习的编码 $e_{[\mathrm{m}]}\in {\mathbb{R}}^D$
6. 现在这个输入的 image patches 就可以表示成：

$$x^{\mathcal{M}}={\left\{{\mathbf{x}}_i^p:i\notin \mathcal{M}\right\}}_{i=1}^N\bigcup {\left\{{\mathbf{e}}_{[M]}:i\in \mathcal{M}\right\}}_{i=1}^N$$

7. 把这个$x^{\mathcal{M}}$ 通过 L 层的 BEIT Encoder，得到 ${\left\{{\mathbf{h}}_i^L\right\}}_{i=1}^N$ ，表示输入image patches的编码表示。
8. 盖住的位置的输出 ${\left\{{\mathbf{h}}_i^L:i\in \mathcal{M}\right\}}_{i=1}^N$，去通过一个分类器，去预测盖住的这个 patch的相应的 visual token

$p_{\mathrm{MIM}}\left(z^{\prime }\mid x^{\mathcal{M}}\right)={\mathrm{softmax}}_{z^{\prime }}\left({\mathbf{W}}_c{\mathbf{h}}_i^L+{\mathbf{b}}_c\right)$

式中 $x^{\mathcal{M}}$ 是盖住之后的所有 image patches， ${\mathbf{W}}_c\in {\mathbb{R}}^{|\mathcal{V}|\times D},{\mathbf{b}}_c\in {\mathbb{R}}^{|\mathcal{V}|}$，这里 |V|=8192 ，D 是模型的 Embedding dimension。

9. BERT 的训练目标是最小化计算预测的 token 与真实的 token 之间的差异，所以BEIT的目标也是最小化计算预测的 token 与真实的 token 之间的差异。在 BEIT 里面，假设我盖住第 i 个patch，毫无疑问它对应的 visual token 应该是 $z_i$ ，这时候我希望 Encoder 输出的第 i 个位置的东西通过分类器之后是 $z_i$ 的概率最大，即：

$$\max \sum _{x\in \mathcal{D}}{E}_{\mathcal{M}}\left[\sum _{i\in \mathcal{M}}\log p_{\mathrm{MIM}}\left(z_i\mid x^{\mathcal{M}}\right)\right]$$

式中， $D$ 是全部的无标签训练数据， $M$ 是随机盖住的位置， $x^M$ 是盖住以后的corrupted image。$i\in \mathcal{M}$ 就是对盖住的每个 patches，BEIT 的 Encoder 在这个位置的输出 ${\mathbf{h}}_i^L$ 通过线性分类器 ${\mathrm{softmax}}_{z^{\prime }}\left({\mathbf{W}}_c{\mathbf{h}}_i^L+{\mathbf{b}}_c\right)$ 之后得到预测的 visual token 与真实 patches 对应的 visual token 越接近越好：

下游任务fine-tuning

拿着训练好的 BEIT Encoder，给它添加一个 分类层 (Linear Transformation)，池化层 (Avg)，和激活函数，只微调分类层 (Linear Transformation)，池化层 (Avg)，和激活函数的参数，Encoder的参数保持不变 BEIT 在下游任务 Fine-tuning

DALLE