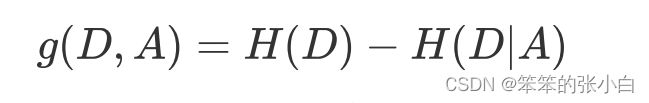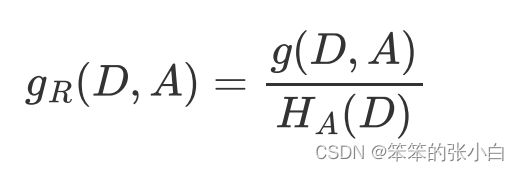决策树原理以及在sklearn中的使用
目录
决策树基础
决策树的ID3和C4.5生成算法
基尼指数与CART决策树
基尼指数(Gini index)
各类算法总结
实战——CART分类树的sklearn实现
实战——决策树解决回归问题
决策树基础
什么是决策树
决策树学习的算法通常是一个递归地选择最优特征(选择方法的 不同,对应着不同的算 法),并根据该特征对训练数据进行分割,使得各个子数据集有一个 最好的分类的过程。这 一过程对应着对特征空间的划分,也对应着决策树的构建。
- 决策树提供了一种展示类似在什么条件下会得到什么值这类规则 的方法
- 决策树一般是自上而下生成的
- 决策树既可以解决分类问题,也可以解决回归问题
信息增益与信息增益比
- 熵(entropy)
熵(entropy)表示随机变量不确定性的度量。设X是一个取有限个 值的离散随机变量,其概率分布为
则随机变量X的熵定义为
- 信息增益
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵 H(D)与特征A给定条件 下D的经验条件熵H(D|A)之差,即
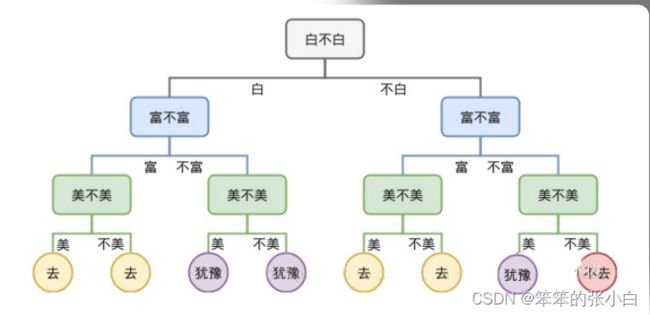
信息增益大的特征具有更强的分类能力,举个例子:
g(D,A2 ),g(D,A3 ),g(D,A4 )的计算方法类似.
- 信息增益比
信息增益值的大小是相对于训练数据集而言的,并没有绝对意 义。当某个特征的取值种 类非常多时,会导致该特征对训练数据集的信息增益偏大。反之, 信息增益值会偏小。使用 信息增益比(information gain ratio)可以对这一问题进行校正。 这是特征选择的另一准 则。 特征A对训练数据集D的信息增益比gR(D,A)定义为其信息增益 g(D,A)与训练数据集D关于 特征A的值的熵HA(D)之比,即
决策树的ID3和C4.5生成算法
- ID3算法生成决策树的核心是在决策树各个结点上应用信息增益准则选择特征,递归地构建决策树
- C4.5在生成决策树的过程中,用信息增益比来选择特征
注意: 决策树生成只考虑了对训练数据更好的拟合,可以通过对决策 树进行剪枝,从而减小模型的复杂度,达到避免过拟合的效果
基尼指数与CART决策树
基尼指数(Gini index)
在分类问题中,假设有K个类,样本点属于第k类的概率为pk, 则概率分布的基尼指数定义为
Gini指数越小表示集合的纯度越高,反之,集合越不纯
例如:有三个类别,它们所占的比例分别为{1/3,1/3,1/3},则基尼 指数为 G=1-(1/3)2-(1/3)2-(1/3)2=0.666;若三个类别所占的比例分别为{1/10,2/10,7/10},则基尼指数 为 G=1-(1/10)2-(2/10)2-(7/10)2=0.46; 若三个类别所占的比例分别为{1,0,0},则基尼指数为 G=1-12=0;
CART决策树
分类与回归树(classification and regression tree,CART) 模型是应用广泛的决策树学习方法。CART既可以用于分类也可以用 于回归。 CART分类树默认使用基尼指数选择最优特征
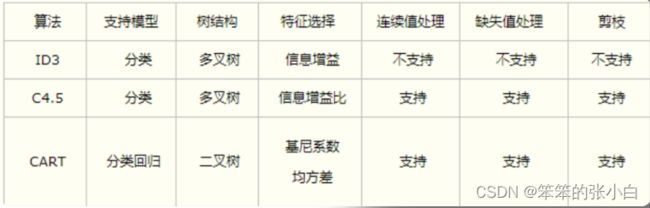
各类算法总结
- ID3:信息增益标示按某种特性分类后,剩余特性的信息熵的大小 的衰减程度,信息熵越小, 证明已经分好的类别就更加的纯粹单一
- C4.5:选择了信息增益比替代信息增益;由于ID3算法会倾向于 选取特征值较多的特征 进行分类(因为这样会让信息增益很大),比如:区分每个学生的成绩 采用学生的学号进行区分,那么每个学生对应一个学号,则按照学 号分的话,每个分组中就只有一个样本,并且信息熵为0,显然这个 不是我们想要的,因此我们引入了信息增益比,每次选择分类特性 的时候,根据信息增益比进行选取
- 基尼系数:代表了模型的不纯度,基尼系数越小,则不纯度越 低,特征越好
实战——CART分类树的sklearn实现
sklearn中使用sklearn.tree.DecisionTreeClassifier可以实现 CART分类树,默认使用gini指数选择特征。
在使用DecisionTreeClassifier对训练数据集进行拟合后,可使 用下面封装的绘图函数进行观察。
# 封装绘图函数
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1],int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3],int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5,cmap=custom_cmap)import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
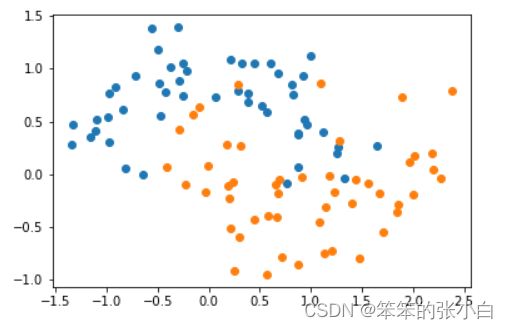
# 生成数据集
X, y = datasets.make_moons(noise=0.25, random_state=666)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()from sklearn.tree import DecisionTreeClassifier
# 测试一
dt_clf1 = DecisionTreeClassifier() # 使用CART分类树的默认参数
dt_clf1.fit(X,y) # 拟合
# 当前训练好的模型绘制决策边界
plot_decision_boundary(dt_clf1,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()通过观察模型拟合结果,发现模型过拟合了,需要调整
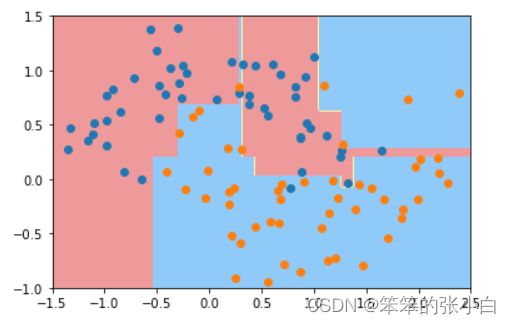
# 测试二
dt_clf2 = DecisionTreeClassifier(max_depth=2) # 设置决策树的最大深度
dt_clf2.fit(X,y) # 拟合
# 当前训练好的模型绘制决策边界
plot_decision_boundary(dt_clf2,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()通过限制决策树的最大深度可以防止过拟合
# 测试三
dt_clf3 = DecisionTreeClassifier(max_leaf_nodes=4) # 设置决策树的最多叶子结点数
dt_clf3.fit(X,y) # 拟合
# 当前训练好的模型绘制决策边界
plot_decision_boundary(dt_clf3,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()通过限制决策树的叶子节点数也可以防止过拟合
实战——决策树解决回归问题
sklearn中使用sklearn.tree.DecisionTreeRegressor可以实现CART 回归树
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston() # 加载波士顿房价数据集
X = boston.data # 样本特征
y = boston.target # 样本标签
# 拆分数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=666)
from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor() # 创建CART回归树对象
dt_reg.fit(X_train,y_train) # 拟合训练集
dt_reg.score(X_test,y_test) # 在测试集上进行测试,R2分数
# DecisionTreeRegressor有很多超参数,可以进行调参达到避免过拟合的效果
dt_reg2 = DecisionTreeRegressor(max_depth=4,max_leaf_nodes=5)
dt_reg2.fit(X_train,y_train) # 拟合训练集
dt_reg2.score(X_test,y_test) # 在测试集上进行测试,R2分数