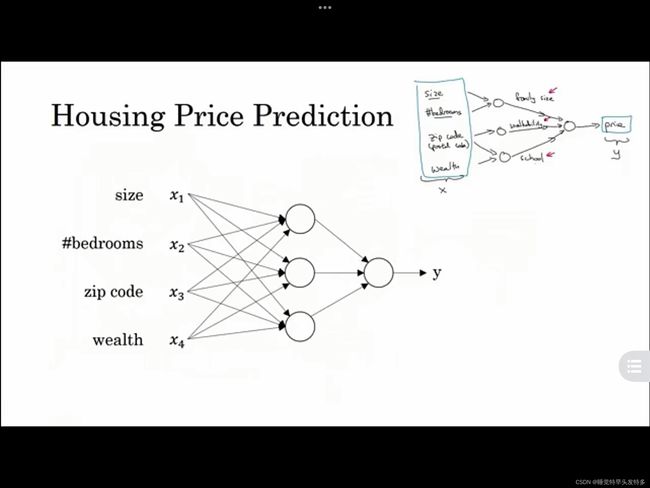
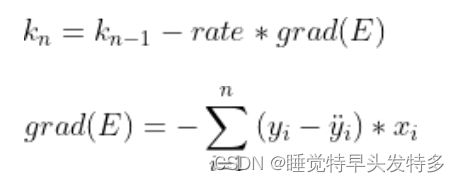13.线性单元和梯度下降 用python求解LMS算法 聚合theta值(出现nan值,已解决)
supervised learning➡️neural networks 神经网络改变了监督学习!
目录
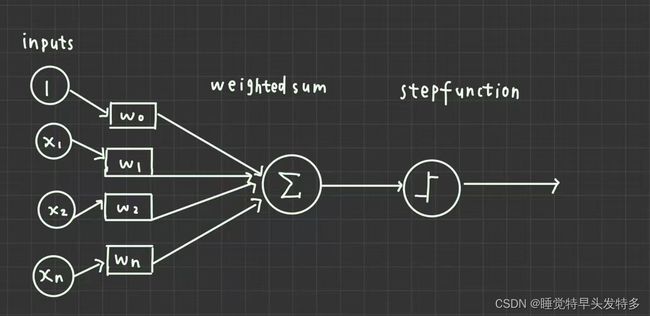
线性单元是什么
线性单元模型
监督学习和无监督学习
梯度下降优化算法
随机梯度下降算法(Stochastic Gradient Descent,SGD)
代码实现
调试过程
本人解决方法
面向过程
面向对象
小结
线性单元是什么
数据集不是线性可分,感知器可能无法收敛,故使用一个可导线性函数(一般选用sigmoid函数)替代step function,
此类感知器是线性单元,其在面对线性不可分的数据集时会收敛到一个最佳的近似上;
线性单元模型:
替换激活函数f后,线性单元将返回一个实数值而不是0、1分类(逻辑回归不是回归方法是分类方法‼️‼️)。因此线性单元用来解决回归问题而不是分类问题。
线性单元模型
![]() 叫做假设,而
叫做假设,而![]() 是它的参数;
是它的参数;
![]() 可能具备多个特征,假设
可能具备多个特征,假设![]() 具备四个特征的向量,所以仅仅一个参数
具备四个特征的向量,所以仅仅一个参数![]() 不够用,如使用四个参数,则
不够用,如使用四个参数,则![]() 的每个特征对应一个参数
的每个特征对应一个参数![]() ,这样模型变为:
,这样模型变为:
监督学习和无监督学习
模型如何训练,即参数如何取值?
当模型“看到”足够多的样本之后,它就能总结出其中的一些规律;然后,就可以预测那些它没看过的输入所对应的答案了。
训练的目的是为了样本的真实值与模型预测值尽可能的接近,而描述这一接近程度的量可以有很多,例如:用差的平方的1/2来表示它们的接近程度(其中![]() 为模型计算出来的预测值,我们希望训练出来的模型预测值和标记值越接近接好。)
为模型计算出来的预测值,我们希望训练出来的模型预测值和标记值越接近接好。)
则模型误差为:
![]()
![]() 为单个样本的误差,乘1/2是为了后面计算方便。训练样本{
为单个样本的误差,乘1/2是为了后面计算方便。训练样本{![]() },其中
},其中![]() 为特征,
为特征,![]() 为标记(label),我们的目标是确定合适的k,从而使得E最小,获得E的局部最优解,这在数学上称作优化问题,
为标记(label),我们的目标是确定合适的k,从而使得E最小,获得E的局部最优解,这在数学上称作优化问题,![]() 是优化目标,称之为目标函数。
是优化目标,称之为目标函数。
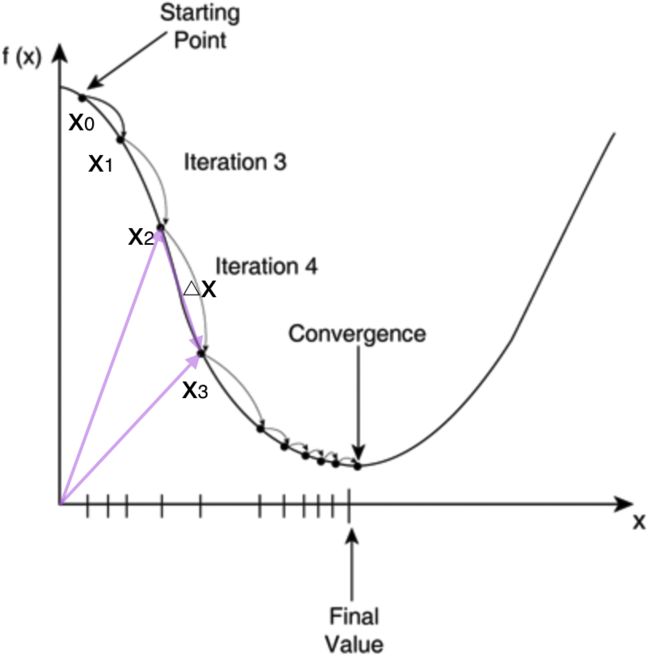
梯度下降优化算法
通过梯度下降(上升)算法求解极小(大)值,学习率rate为步长。梯度下降算法(Gradient Descent Alogrithm)是沿梯度下降的方向连续迭代逼近求最小值的过程。
随机梯度下降算法(Stochastic Gradient Descent,SGD)
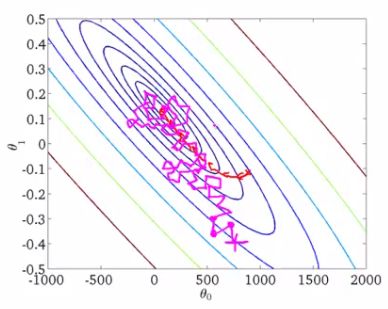
批梯度下降(BGD)每次更新k需要遍历一遍所有参数,效率极低;
随机梯度下降(SGD)每次随机选取一个样本来更新k,效率较高;
如上图,椭圆表示的是函数值的等高线,椭圆中心是函数的最小值点。红色是BGD的逼近曲线,而紫色是SGD的逼近曲线。我们可以看到BGD是一直向着最低点前进的,而SGD明显躁动了许多,但总体上仍然是向最低点逼近的。
最后需要说明的是,SGD不仅仅效率高,而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』,沿着梯度反方向就能找到全局唯一的最小值。然而对于非凸函数来说,存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值,从而获得一个更好的模型。
代码实现
随机梯度下降训练速度很快,而批梯度下降在样本很多的时候,训练效率极低! 只需在循环体内稍作改动:x = random.randint(0,4)从五组数据中随机选取一组数据进行迭代便可实现BGD➡️SGD
Structured Data⬇️
Standard NN
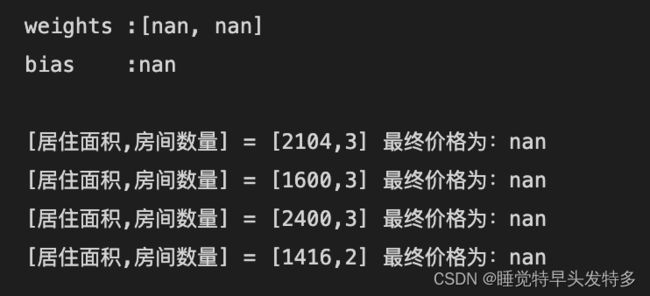
调试过程
没有报错但出现nan值➡️
某一步骤计算结果出现0/exp/学习率设置过高/log函数出现负数值或者0/数据质量不高
列表取片操作易错点(list indices must be integers or slices, not tuple原因及解决方法)_Pika_T的博客-CSDN博客
matlab里神经网络预测值出现了负值怎么办? - 知乎
卷积神经网络中loss值为nan的问题(已解决)_喵嗷的博客-CSDN博客_loss值是nan
本人解决方法
经历了三天的各种调试过程,修改激活函数、修改迭代次数和学习率,最终价格有时为nan值,有时为负值,有时为数值很大很大的正值;
:
(1)第一列数据除以1000,第三列数据除以100;
(2)每一列数据都除以它的第一行数据;
(3)数据归一化处理
tensorflow预处理:数据标准化的几种方法_chary8088的博客-CSDN博客_tensorflow 标准化
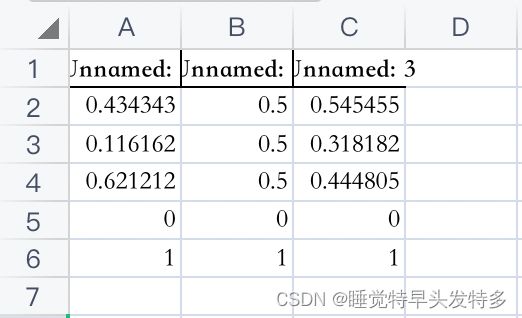
初始数据:
| 2104 | 3 | 400 |
| 1600 | 3 | 330 |
| 2400 | 3 | 369 |
| 1416 | 2 | 232 |
| 3000 | 4 | 540 |
(0,1)标准化处理后的数据:
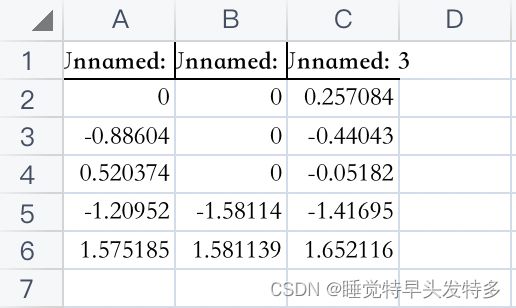
Z-score标准化处理后的数据:
面向过程
代码实例:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import random
import matplotlib.pyplot as plt
x = np.array([[2104,3], [1600,3], [2400,3], [1416,2],[3000,4]])
t = np.array([400,330,369,232,540])
alpha = 0.1 #学习率
theta0 = np.random.random()
theta1 = np.random.random()
theta2 = np.random.random()
theta=np.array([theta1,theta2])
eps = 1e-4 #防止出现0
for i in range(0,2):
e0 = 0.5 * (np.sum((x[:, i] * theta[i])) + theta0 - t[i])
e1 = e0 * x[1, i]
e2 = e0 * x[2, i]
while e0 >= eps or e1 >= eps or e2 >= eps:
x=random.randint(0,4) #从5组数据中随机选取一组进行迭代
i=0
theta0 = theta0 - alpha * e0
theta1 = theta1 - alpha * e1
theta2 = theta2 - alpha * e2
i+=1
print(theta0, theta1, theta2)
fig1=plt.figure() #创建一个绘图对象
ax=Axes3D(fig1) #用这个绘图对象创建一个Axes对象
X1,X2=np.mgrid[0:10000:500j, 0:50:500j] # 从0到10000生成500个房间平米数X1,从0到50生成500个房间数X2
h=theta0+(theta1*X1+theta2*X2)
plt.title("Housing Price Prediction Graph") #图像标题
ax.plot_surface(X1, X2, h , rstride=1, cstride=1, cmap=plt.cm.coolwarm, alpha=0.5) #用取样点(x1,x2,h)去构建曲面
ax.set_xlabel('X1 Living area', color='red')
ax.set_ylabel('X2 #Bedrooms', color='blue')
ax.set_zlabel('h Price', color='green')
plt.show()#显示模块中的所有绘图对象
运行结果:
先后为theta0 theta1 theta2
0.17632249350854468 0.8253948844830631 0.5947541888493746
0.09353650544741843 0.776589914587936 0.43193121485307107
面向对象
代码实例: practice/a0929-4.py
from functools import reduce
import numpy as np
#定义感知器类
class perceptron(object):
#感知器初始化函数(参数个数,激活函数)
def __init__(self, input_num, activator):
self.activator = activator
self.weights = [0.0 for _ in range(input_num)] #将每个参数对应权值设为0
self.bias = 0.0 #偏置值设为0
#输出训练所得权值与偏置值
def __str__(self):
return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)
#计算激活函数值
def predict(self, input_vec):
return self.activator(reduce(lambda a, b : a + b, map(lambda xw : xw[0] * xw[1], zip(input_vec, self.weights)), 0.0) + self.bias)
#更新权重与偏置值
def _update_weights(self, input_vec, output, label, rate):
delta = label - output #计算预测值与真值之差
self.weights = list(map(lambda xw : xw[1] + rate * delta * xw[0], zip(input_vec, self.weights))) #更新权重
self.bias = rate + delta #更新偏置
#迭代计算
def _one_iteration(self, input_vecs, labels, rate):
samples = zip(input_vecs, labels)
for(input_vec, label) in samples:
output = self.predict(input_vec) #计算激活函数值
self._update_weights(input_vec, output, label, rate) #更新权值与偏置值
#训练数据得权值、偏置值
def train(self, input_vecs, labels, iteration, rate):
for _ in range(iteration):
self._one_iteration(input_vecs, labels, rate)
#定义激活函数
def f(x):
return x
#构建训练集
#def get_training_dataset():
# input_vecs = [[0.2104,3],[0.1600,3],[0.2400,3],[0.1416,2],[0.3000,4]]
# labels = [0.400,0.330,0.369,0.232,0.540]
# return input_vecs, labels
#def get_training_dataset():
input_vecs = [[0,0],[-0.886041760444641,0],[0.520373702049255,0],[-1.20951724052429,-1.58113884925842],[1.57518529891968,1.58113884925842]]
labels = [0.257084310054779,-0.440431356430054,-0.0518154688179493,-1.41695320606232,1.65211570262909]
return input_vecs, labels
def get_training_dataset():
input_vecs = [[0.434343457221985,0.5],[0.116161584854126,0.5],[0.621212124824524,0.5],[0,0],[1,1]]
labels = [0.545454561710358,0.318181812763214,0.444805204868317,0,1]
return input_vecs, labels
#构建训练集训练感知器
def train_linear_unit():
p = perceptron(2, f)
input_vecs, labels = get_training_dataset()
p.train(input_vecs, labels, 40, 0.01)
return p
#主函数
if __name__ == '__main__':
linear_unit = train_linear_unit()
print(linear_unit)
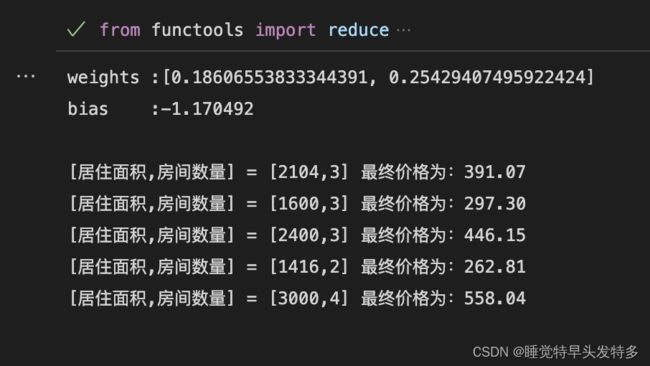
print('[居住面积,房间数量] = [2104,3] 最终价格为:%.2f' % linear_unit.predict([2104,3]))
print('[居住面积,房间数量] = [1600,3] 最终价格为:%.2f' % linear_unit.predict([1600,3]))
print('[居住面积,房间数量] = [2400,3] 最终价格为:%.2f' % linear_unit.predict([2400,3]))
print('[居住面积,房间数量] = [1416,2] 最终价格为:%.2f' % linear_unit.predict([1416,2]))
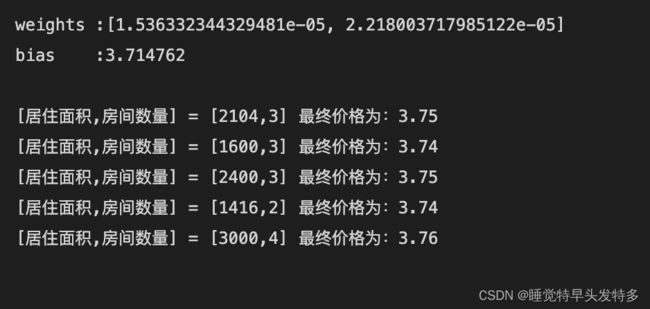
print('[居住面积,房间数量] = [3000,4] 最终价格为:%.2f' % linear_unit.predict([3000,4]))
运行结果:
小结
(1)数据本身的质量和数据样本大小都会直接影响训练模型的拟合程度~
(2)没有固定的方法,即便是很相似的模型,具体的解决方法也有很大的不同,多尝试,多比较~
(3)多推导公式,多敲代码~