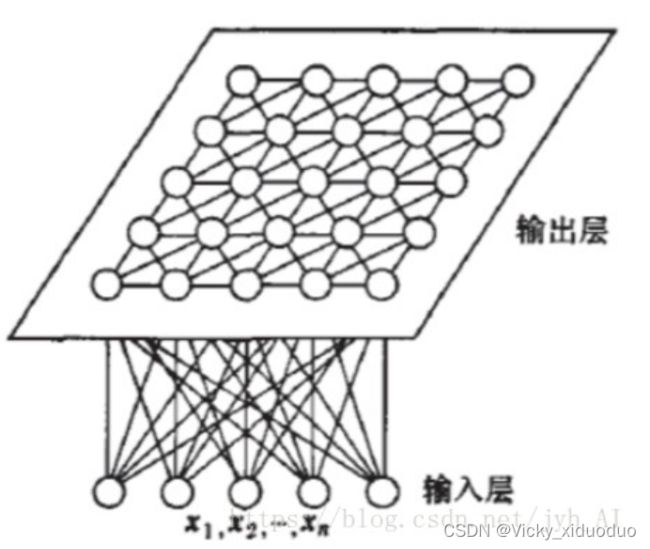
机器学习算法——神经网络6（SOM网络）
SOM（Self-Organizing Map,自组织映射）网络也是一种竞争学习型的无监督神经网络。
它能将高维数据映射到低维空间（通常为二维），同时保持输入数据在高维空间的拓扑结构，即将高维数据中相似的样本点映射到网络输出层中的邻近神经元。
SOM网络结构为：
输入层神经元的数量是由输入向量的维度决定的，一个神经元对应一个特征。
输出层中的一个节点代表一个需要聚成的类。
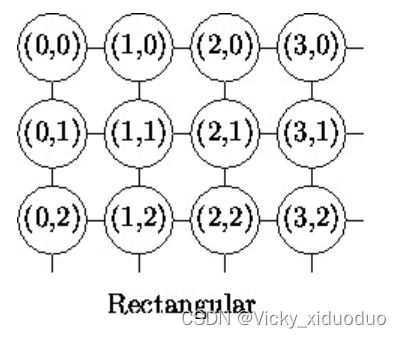
SOM网络结构的区别主要在竞争层：可以有1维、2维（最常见）。竞争层也可以有更高的维度，不过处于可视化的目的，高维竞争层用的比较少。输出层中的节点与输入层的节点是全连接的。
其中二维平面有2种平面结构，即
竞争层SOM神经元的数量决定了最终模型的粒度与规模，这对最终模型的准确性与泛化能力影响很大。
根据查找的资料，有人得出一条经验公式：竞争层最少节点数量=
,N是训练样本的个数。如果是正方形输出，边长等于竞争层节点数再开一次根号，并向上取整即可。
SOM网络中的输出层神经元以矩阵方式排列在二维空间中，每个神经元都拥有一个权向量，网络在接收输入向量后，将会确定输出层获胜神经元，它决定了该输入向量在低维空间中的位置。
SOM的训练过程：在接收到一个训练样本后，每个输出层神经元会计算该样本与自身携带的权向量之间的距离，距离最近的神经元成为竞争获胜者，称为最佳匹配单元。然后最佳匹配单元及其邻近神经元的权向量将被调整，以使这些权向量与当前输入样本的距离缩小。这个过程不断迭代，直至收敛。
SOM的主要目标是将任意维度的输入信号模式转换为一维或二维离散映射，并以拓扑有序的方式自适应地执行这种变换。
SOM网采用的算法称为Kohonen算法，在“胜者通吃”（Winner-Talk-All,WTA）学习规则上加以改进的，主要区别是调整权向量与侧抑制的方式不同：
WTA：侧抑制是封杀式的，只有获胜神经元可以调整其权值，其他神经元都无权调整。
Kohonen算法：获胜的神经元对其邻近神经元的影响是由近及远，由兴奋逐渐变为抑制。即，不仅获胜神经元要调整权值，它周围的神经元也要不同程度调整权向量。
常见的调整方式有：
①墨西哥草帽函数：获胜节点有最大的权值调整量，邻近的节点有稍小的调整量，离获胜节点距离越大，权值调整量越小。直到某一距离d0时，权值调整为零。当距离再远一些时，权值调整量稍负，更远又回到零。如图a所示。
②大礼帽函数：他是墨西哥草帽函数的一种简化。如图b所示。
③厨师帽函数：它是大礼帽函数的一种简化，如图c所示。
以获胜神经元为中心设定一个邻域半径R，该半径固定的范围称为优胜邻域。在SOM网学习方法中，优胜邻域内的所有神经元，均按其与获胜神经元距离的远近不同程度调整权值。优胜邻域开始定的较大，但其大小随着训练次数的增加不断收缩，最终收缩到半径为零。
SOM算法学习的过程为：
（1）初始化：对输出层各权向量赋小随机数并进行归一化处理，得到
(j=1,2,...,m)，m为输出层神经元数目。建立初始优胜邻域
和学习率
初值。
（2）接受输入：从训练集中随机取一个输入模式并进行归一化处理，得到
(p=1,2,...,n)，n为输入层神经元数目。
（3）寻找获胜节点
计算与的点积，从而找到点积最大的获胜节点j*
（4）定义优胜邻域
以j*为中心确定t时刻的权值调整域。
（5）调整权值
对优胜邻域内的所有节点调整权值
![w_{ij}(t+1) = w_{ij}(t)+\eta (t,N)[x_i^P-w_{ij}(t)]](http://img.e-com-net.com/image/info8/fd2d9ce3a4ea41578aeca1d94021187f.gif){kind=small}
, i=1,2,...,n, 
是训练时间t和邻域内第j个神经元与获胜神经元j*之间的拓扑距离N的函数。该函数一般有以下规律：t⬆➡η⬇，N⬆➡η⬇，可以选择指数衰减，即
（6）结束判定
当学习率α(t)≤αmin时，训练结束；不满足结束条件时，转到步骤（2）继续。（结束条件其实为学习率衰减为0。）
SOM与KMeans算法相似，所不同的是，SOM网络不需要预先提供聚类数量，类别的数据由网络自动识别出来。
讲完理论，然后讲Python代码实现SOM算法，用到的数据集为Iris数据集。
首先导入所需要的库：
# coding=utf-8
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from minisom import MiniSom
from sklearn.metrics import classification_report
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
import math主函数：
if __name__ == '__main__':
# 数据准备
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_names
#划分数据集
X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.3, random_state=100)
#训练Som模型
#样本数量
N = X_train.shape[0]
#维度/特征数量
M = X_train.shape[1]
#设置超参数
size = math.ceil(np.sqrt(5*np.sqrt(N))) #向上取整,经验公式，决定输出层尺寸
print("训练样本个数：{} 测试样本个数：{}".format(N, X_test.shape[0]))
print("输出网格最佳边长：", size)
max_iter = 400
som = MiniSom(size, size, M, sigma=3, learning_rate=0.5, neighborhood_function='bubble')
#初始化权值，有2个API
# som.random_weights_init(X_train)#带有一定的随机性
som.pca_weights_init(X_train)#pca初始化的结果是固定的，也就是说网络初始状态是固定的。
som.train_batch(X_train, max_iter, verbose=False)#每次按顺序取一个样本，用过最后一个样本后跳回第一个样本，
#循环直到迭代次数满足max_iter
#som.train_random(X_train, max_iter, verbose=False)每次迭代随机挑选一个样本来更新权重，直到迭代次数满足max_iter
#分类
winmap = som.labels_map(X_train, Y_train)#返回一个双层字典，反映每个神经元收集到的标签种类，及每个标签下的样本个数
print(winmap)#一个是神经元的坐标，一个是列表中每个元素出现的次数。
y_pred = classify(som, X_test, winmap)
print(classification_report(Y_test, np.array(y_pred), target_names=target_names))
#第一种可视化
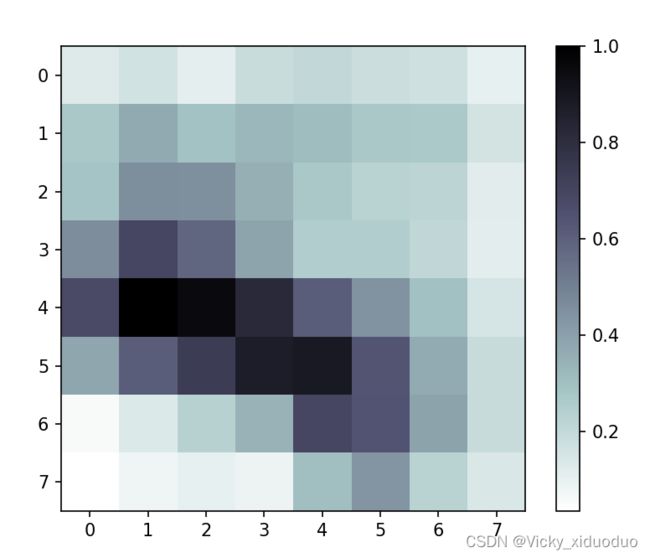
#根据权重矩阵w，可以计算每个神经元距离他最近的邻近神经元的距离，计算好的矩阵就是U-Matrix
# heatmap = som.distance_map()#生成U-Matrix
# plt.imshow(heatmap, cmap='bone_r')
# plt.colorbar()
# plt.show()
#第二种可视化方案
label_name_map_number = {"setosa": 0, "versicolor": 1, "virginica": 2}
the_grid = GridSpec(size, size)
for position in winmap.keys():
label_fracs = [winmap[position][label] for label in [0, 1, 2]]
plt.subplot(the_grid[position[1],position[0]],aspect=1)
patches, texts = plt.pie(label_fracs)
plt.text(position[0]/100, position[1]/100, str(len(list(winmap[position].elements()))),
color='black', va='center', ha='center')
plt.legend(patches, target_names, loc='center right', bbox_to_anchor=(-1,8), ncol=3)
plt.show()主函数中用到了分类函数classify，具体实现如下：
#分类函数
def classify(som, data, winmap):
default_class = np.sum(list(winmap.values())).most_common()[0][0]
print(np.sum(list(winmap.values())))
result = []
for d in data:
win_position = som.winner(d)
if win_position in winmap:
result.append(winmap[win_position].most_common()[0][0])
else:
result.append(default_class)
return result最后得到som算法的可视化结果，第一种可视化结果为（a）,第二种可视化结果为(b)
(a) (b)
（a）是权重矩阵可视化。
(b)中在每个格子里画饼图，且用颜色表示类别，用数字表示总样本数量。