torch.stack, torch.cat, torch.stack.max/mean/sum维度变换详解

---

学习pytorch时，总免不了遇到stack和cat操作，或者有时候搞不清楚stack后max/mean/sum的操作原理。我通过代码实验为大家解说一些这些操作的原理。

---

torch.stack

torch.stack说白了原理也是来自于numpy.satck的操作。
主要接受两个参数：
一个数组（包含了具有相同维度的tensor元素）；
一个维度（制定了堆叠的维度位置）

一般因为我们深度学习中一般都是会用到四个维度信息，所以在这里我们也以创建具有四个维度信息的tensor变量来做说明。

创建两个[x,x,x,x]tensor变量

import torch
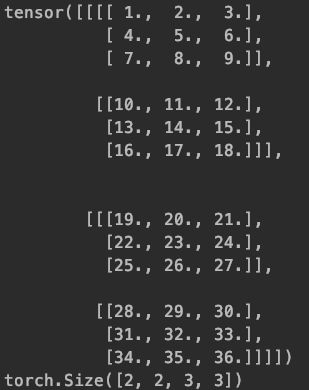
a = torch.FloatTensor([[[[1,2,3],[4,5,6],[7,8,9]],[[10,11,12],[13,14,15],[16,17,18]]]])
b = torch.FloatTensor([[[[19,20,21], [22,23,24],[25,26,27]],[[28,29,30],[31,32,33],[34,35,36]]]])
print(a, b, a.data.shape, b.data.shape, sep='\n')

shape信息都是[1, 2, 3, 3]

---

torch.stack([x,x], dim=0)

对于四维信息，可以指定dim=0-4共五个维度进行堆叠。

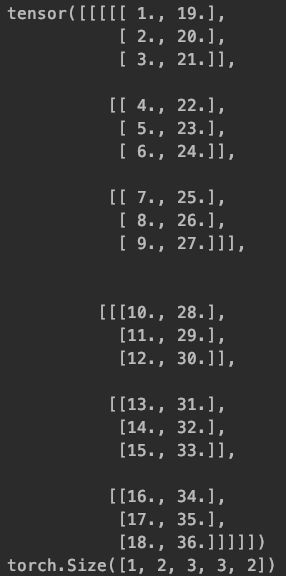
c=torch.stack([a,b], dim=0)
print(c, c.data.shape, sep='\n')

shape信息变为[2, 1, 2, 3, 3]
在堆叠之后的tensor第一个维度将两个tensor（a和b）堆叠
其实就是相当于直接:
c=[a, b], shape为[2, 1, 2, 3, 3]，如此改变了第一个维度信息，即dim=0；

---

torch.stack([x,x], dim=1)

c=torch.stack([a,b], dim=1)
print(c, c.data.shape, sep='\n')

shape信息变为[1, 2, 2, 3, 3]
在堆叠之后的tensor第二个维度将两个tensor（a和b）堆叠
其实就是相当于:
a=（a去掉最外侧维度信息），就是变为[2,3,3]
b=（b去掉最外侧维度信息），就是变为[2,3,3]

c=[a,b]， shape为[2, 2, 3, 3]，如此改变了第二个维度信息，即dim=1；

c=[c]=[[a,b]], shape为[1, 2, 2, 3, 3]，恢复dim=0时的1维度信息；

---

torch.stack([x,x], dim=2)

c=torch.stack([a,b], dim=2)
print(c, c.data.shape, sep='\n')

shape信息变为[1, 2, 2, 3, 3]
在堆叠之后的tensor第三个维度将两个tensor（a和b）堆叠
其实就是相当于:
a=（a去掉外侧维度信息），就是变为两个tensor， a1=[3,3]， a2=[3,3]；
b=（b去掉外侧维度信息），就是变为两个tensor， b1=[3,3]， b2=[3,3]；

c1=[a1,b1], 如此改变了第三个维度信息，shape为[2, 3, 3]， 即dim=2
c2=[a2,b2], 如此改变了第三个维度信息，shape为[2, 3, 3]， 即dim=2

c=[c1, c2]， shape为[2, 2, 3, 3]. 恢复dim=1时的2维度信息。
c=[c]=[[c1,c2]], shape为[1, 2, 2, 3, 3].恢复dim=0时的1维度信息。

---

torch.stack([x,x], dim=3)

c=torch.stack([a,b], dim=3)
print(c, c.data.shape, sep='\n')

shape信息变为[1, 2, 2, 3, 3]
在堆叠之后的tensor第四个维度将两个tensor（a和b）堆叠
其实就是相当于:
a=（a去掉外侧维度信息），就是变为六个tensor：
a1=[3]， a2=[3]，a3=[3]， a4=[3]，a5=[3]， a6=[3]；
b=（b去掉外侧维度信息），就是变为六个tensor：
b1=[3]， b2=[3]，b3=[3]， b4=[3]，b5=[3]， b6=[3]；

c1=[a1,b1], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3
c2=[a2,b2], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3
c3=[a3,b3], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3
c4=[a4,b4], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3
c5=[a5,b5], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3
c6=[a6,b6], 如此改变了第四个维度信息，shape为[2, 3]， 即dim=3

c1=[c1,c2,c3] ， shape 为[3, 2, 3]. 恢复dim=2时的3维度信息；
c2=[c4,c5,c6]， shape 为[3, 2, 3]. 恢复dim=2时的3维度信息；

c=[c1, c2]， shape为[2, 2, 3, 3]. 恢复dim=1时的2维度信息；
c=[c]=[[c1,c2]], shape为[1, 2, 2, 3, 3]. 恢复dim=0时的1维度信息；

---

torch.stack([x,x], dim=4)

c=torch.stack([a,b], dim=4)
print(c, c.data.shape, sep='\n')

shape信息变为[1, 2, 2, 3, 3]
在堆叠之后的tensor第五个维度将两个tensor（a和b）堆叠
其实就是相当于:
a=（a去掉外侧维度信息），就是变为18个值：
a1=1， a2=2，a3=3， a4=4，a5=5， a6=6…；
b=（b去掉外侧维度信息），就是变为18个值：
b1=19， b2=20，b3=21， b4=22，b5=23， b6=24…；

c1=[a1,b1], 如此改变了第 五个维度信息，shape为[2]， 即dim=4
c2=[a2,b2], 如此改变了第五个维度信息，shape为[2]， 即dim=4
c3=[a3,b3], 如此改变了第五个维度信息，shape为[2]， 即dim=4
c4=[a4,b4], 如此改变了第五个维度信息，shape为[2]， 即dim=4
c5=[a5,b5], 如此改变了第五个维度信息，shape为[2]， 即dim=4
c6=[a6,b6], 如此改变了第五个维度信息，shape为[2]， 即dim=4
…

c1=[c1,c2,c3] ， shape 为[3, 2]. 恢复dim=3时的3维度信息；
c2=[c4,c5,c6]， shape 为[3, 2]. 恢复dim=3时的3维度信息；
c3=[c7,c8,c9] ， shape 为[3, 2]. 恢复dim=3时的3维度信息；
c4=[c10,c11,c12]， shape 为[3, 2]. 恢复dim=3时的3维度信息；
c5=[c13,c14,c15] ， shape 为[3, 2]. 恢复dim=3时的3维度信息；
c6=[c16,c17,c18]， shape 为[3, 2]. 恢复dim=3时的3维度信息；
…

c1=[c1, c2, c3]，shape 为[2, 3, 2]. 恢复dim=2时的3维度信息；
c2= [c4, c5, c6]，shape 为[2, 3, 2]. 恢复dim=2时的3维度信息；

c=[c1, c2 ]， shape为[2, 3, 3, 2]. 恢复dim=1时的2维度信息；
c=[c]=[[c1,c2]], shape为[1, 2, 2, 3, 3]. 恢复dim=0时的1维度信息；

简单总结

就是stack操作是将tensor先拆解到指定的维度上，再该维度上进行堆叠，然后逐渐恢复之前的维度信息。

torch.cat

对于四维信息，可以指定dim=0-3共四个维度进行concat。

c = torch.cat([a, b],dim=0)  #两个的每一列加在一起
print(c, c.data.shape, sep='\n')
c = torch.cat([a, b],dim=1)  #两个的每一列加在一起
print(c, c.data.shape, sep='\n')
c = torch.cat([a, b],dim=2)  #两个的每一列加在一起
print(c, c.data.shape, sep='\n')
c = torch.cat([a, b],dim=3)  #两个的每一列加在一起
print(c, c.data.shape, sep='\n')

原理和stack感觉差不多，只不过stack是堆叠出一个新的维度信息，由4个维度变为五个维度，而cat是四个维度依然是四个维度，只不过制定维度位置上的channels直接进行了翻倍或者多倍。

---

torch.cat([x,x], dim=0)

shape信息变为[2, 2, 3, 3]
其实就是相当于直接:
a=[2,3,3]
b=[2,3,3]
c=[a, b], shape为[2, 2, 3, 3]，如此翻倍了第一个维度信息，即dim=0；

torch.cat([x,x], dim=1)

shape信息变为[1, 4, 3, 3]
其实就是相当于直接:
a1=[3,3]，a2=[3,3]
b1=[3,3]，b2=[3,3]，
c=[a1,a2,a3,a4], shape为[4, 3, 3]，如此翻倍了第二个维度信息，即dim=1；
c=[c], 恢复第一个维度信息1，shape为[1, 4, 3, 3]

torch.cat([x,x], dim=2)

shape信息变为[1, 2, 6, 3]
其实就是相当于直接:
a=（a去掉外侧维度信息），就是变为六个tensor：
a1=[3]， a2=[3]，a3=[3]， a4=[3]，a5=[3]， a6=[3]；
b=（b去掉外侧维度信息），就是变为六个tensor：
b1=[3]， b2=[3]，b3=[3]， b4=[3]，b5=[3]， b6=[3]；
c1=[a1,a2,a3,b1,b2,b3], shape为[6, 3]，如此翻倍了第三个维度信息，即dim=2；
c2=[a4,a5,a6,b4,b5,b6], shape为[6, 3]，如此翻倍了第三个维度信息，即dim=2；
c=[c1,c2], 恢复第二个维度信息2，shape为[2, 6, 3]
c=[c], 恢复第一个维度信息1，shape为[1, 2, 6, 3]

torch.cat([x,x], dim=3)

a=（a去掉外侧维度信息），就是变为18个值：
a1=1， a2=2，a3=3， a4=4，a5=5， a6=6…；
b=（b去掉外侧维度信息），就是变为18个值：
b1=19， b2=20，b3=21， b4=22，b5=23， b6=24…；

然后先将a1,a2,a3,b1,b2,b3放入一个[]，翻倍了维度，
如此进行，一共将6个[]进行了翻倍，shape为[6]
再将前三个放入[], 恢复第3个维度信息, shape为[3, 6]
再将得到的两个[]放入[], 恢复第2个维度信息, shape为[2, 3, 6]
再将得到的一个[]放入[], 恢复第1个维度信息, shape为[1, 2, 3, 6]

torch.stack([x, x],dim=x).max(dim)

max中的dim也可以指定dim。
我们以torch.stack([a, b],dim=1).max(dim) 来解说一下操作。
同样对于max，其中的维度可以指定五个（对于四个维度信息来说）

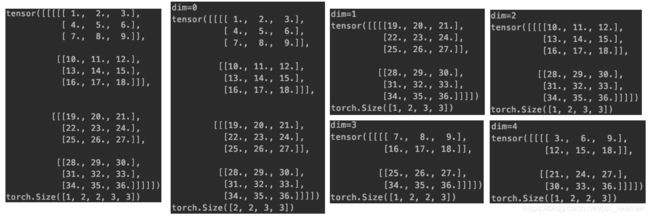
c,_=torch.stack([a,b], dim=1).max(0)
print('dim=0 ', c, c.data.shape, sep='\n')
c,_=torch.stack([a,b], dim=1).max(1)
print('dim=1 ', c, c.data.shape, sep='\n')
c,_=torch.stack([a,b], dim=1).max(2)
print('dim=2 ', c, c.data.shape, sep='\n')
c,_=torch.stack([a,b], dim=1).max(3)
print('dim=3 ', c, c.data.shape, sep='\n')
c,_=torch.stack([a,b], dim=1).max(4)
print('dim=4 ', c, c.data.shape, sep='\n')

其实就是在相应的维度上找最大值，然后维度信息会恢复到堆叠前的维度信息。

---

torch.stack([x, x],dim=x).mean(dim)

mean中的dim也可以指定dim。
我们以torch.stack([a, b],dim=1).mean(dim=1) 来解说一下操作。
同样对于mean，其中的维度可以指定五个（对于四个维度信息来说）

c=torch.stack([a,b], dim=1).mean(1)
print('dim=1 ', c, c.data.shape, sep='\n')

其实就是在相应的维度上进行element-wise加和，再取average，然后维度信息会恢复到堆叠前的维度信息。

torch.stack([x, x],dim=x).sum(dim)

sum中的dim也可以指定dim。
我们以torch.stack([a, b],dim=1).sum(dim=1) 来解说一下操作。
同样对于sum，其中的维度可以指定五个（对于四个维度信息来说）

c=torch.stack([a,b], dim=1).sum(1)
print('dim=1 ', c, c.data.shape, sep='\n')

其实就是在相应的维度上进行element-wise加和，不再取average，然后维度信息会恢复到堆叠前的维度信息。

---

2020.03.25

---