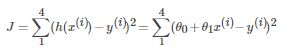详解梯度下降法求解线性模型参数

有监督学习和无监督学习

机器学习，分为有监督学习和无监督学习。
有监督学习，就是有训练集，有label，我们是可以知道模型输出是什么样子的。而无监督学习，没有训练集，没有label，提前无法知道输出的样子。
有监督学习分为两种：回归和分类。模型输出若为连续变量，就是回归；模型输出为离散值，就是分类。
无监督学习常见的是聚类。给定一堆数据集，从中找出相似的类簇，这个过程没有label。

神经网络，深度学习，SVM和决策树，都是有监督学习。下面介绍的方法也只适用于有监督学习。

模型

机器学习最一般的模型就是下面这个图。

给定m个训练集，每个训练集有n个特征。训练集作为X输入给模型，经过训练后模型就是h(x)。
线性模型的求解，就是求解h(x)表达式的过程。

线性模型的表示

线性模型的表达式为

hθ(x)=θ0+θ1x1+θ2x2+…+θnxn

[1]
其中
x1~xn就是n个特征，作为模型的输入
θ0~θn，就是线性模型的n+1个参数

根据m个训练集，求解θ0_{θn的具体数值的过程，就是所谓的学习。求解线性模型，就是求其参数θ0}θn的解。

线性模型求解思路

我们当然是希望求解出来的模型，预测值尽量逼近真实值。

为了更为直观的说明线性模型，以最简单的线性模型hθ(x)=θ0+θ1x为例，用下图表示，红色点为训练集。

图中有4(m)个训练集，h(x)是最终求得的模型。

我们希望模型的预测值与真实值之间的差别，尽量的小。用欧氏距离来表示：
J=(h(x(1))−y(1))2+(h(x(2))−y(2))2+(h(x(3))−y(3))2+(h(x(4))−y(4))2

[2]
其中 x(1)，和y(1)表示第一个训练集的特征，和真实值

J 更一般的表达式为

[3]
这里的预测值与真实值之间的欧氏距离之和J，就是所谓的代价函数。找到能使代价函数最小值点的参数θ，就是线性模型的解。

代价函数

代价函数的定义如下

[4 ]
它的物理含义就是预测值与真实值之间的差别。差别越小，就说明我们的模型和真实模型越接近。代价函数J是其参数θ的二次函数。代价函数的表达式，就是均方差MSE（Mean Square Error）的定义。

这里还是用简化的线性模型来说明问题，另式[3]中的θ1=0和y(i)=1，可得代价函数的曲线为

这里把代价函数看成曲线，是最简单的情况。代价函数更多情况下是以多维曲面的形态出现的（曲面也有最低点）。

梯度下降法

图3中，代价函数的最小值是其导数为零的点。

在图中任意取一个θ值作为其初始值，然后不断迭代最终找到代价函数导数为0点（最小值）的过程，就是求解代价函数参数θ的过程（学习），也就是梯度下降法的物理含义。它的思想为，只要顺着梯度方向下降迭代，就能找到代价函数的最小值。

对于代价函数是多维曲面的情况，可以把曲面类比成山，想象梯度下降法就是从山上往下走，每一步顺着梯度方向，最终肯定就能走到山谷最低点。

无论是曲线还是曲面，会不会有多个局部最低点呢？答案是会的，梯度下降法很可能找不到真正的最低点，它可能只能找到局部最低点。

但好消息是，线性模型的代价函数，在数学上已经被证明为凸函数，即这种函数的局部最低点就是其最低点。所以我们在线性模型中用梯度下降思路求解最小值是没有问题的。

最小均方算法

最小均方算法``LMS(Least Mean Square)是梯度下降思想的具体实现，它是由Bernard Widrow和Marcian E. Hoff提出的，所以也叫Widrow-Hoff学习规则。

为什么叫最小均方呢，这是因为代价函数的表达式，就是均方差``MSE（Mean Square Error）的定义。

LMS算法是这样的

Repeat until convergence (for every j){

[5]
}(update θj simultaneously)

其中

			θj表示线性模型的某一个参数
			:=是赋值符号
			α表示学习速率
			convergence是收敛

它说明，为了求得任意一个参数θj的值，首先我们需要对θj取一个初值，然后顺着代价函数J的梯度方向（ ∂/∂θj）不断迭代，直到θj的值收敛（即本次迭代和上次迭代的值为同一个），就找到了θj的值。

对每一个参数都一起进行这个迭代过程，就能求得每一个参数的值。不过这里要注意的是，要结束一轮迭代后，才对各个参数的值做更新。

这里要注意的是学习速率α，它会把梯度值放大。所以学习速率越大，寻找代价函数最小值过程中迭代的步长也就越大。

1.学习速率太大，有可能导致参数不收敛，或收敛到最后震荡较大
2.学习速率太小，则肯定会收敛，但收敛迭代次数会很大
3.一般情况下，每一次迭代后，梯度都会变小。所以即便学习速率是固定值，学习步长也会随着迭代次数增加而减小

代价函数的形状也与各个特征x的大小相关，为了让代价函数形状均衡，一般要对特征做归一化（比如-1）

最小均方算法的一般化表达推导

将代价函数的表达式[4]带入LMS算法式[5]中的α∂/∂θjJ(θ)，用偏微分对表达式化简，可得

[6]
将线性模型的表达式[1]带入[6]中的∂/∂θj(h(x(i))−y(i))

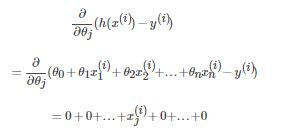
[7]
所以，式[6]可简化为

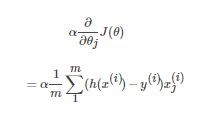
[8]
将式[8]带入LMS算法表达式[5]中，可得LMS算法的一般化表达式为

Repeat until convergence (for every j){

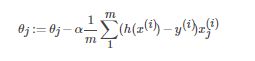
[9]
}(update θj simultaneously)

参考

【1】Andrew NG. machine learning class at coursera