基于PARK-Clark的双闭环PI的永磁同步电机SVPVM控制系统simulink仿真

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

一、理论基础

      SVPWM算法很适合在数字系统中使用，有很高的直流电压利用率，而且可以有效降低电机的转矩脉振和噪音，其基本结构如下：

      

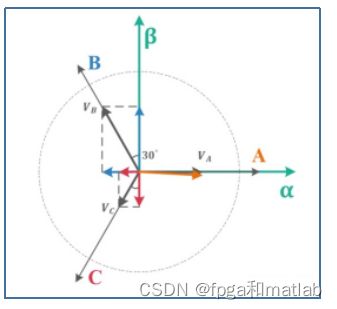
      三相静止ABC坐标系下的交流信号跟踪问题，在经过Clark变换和Park变换后，转换为两相旋转坐标系下的直流信号跟踪问题，于是，同志们又可以愉快的使用PID控制了。

      瞬时空间磁链矢量圆轨迹法(SVPWM)就是在很短的一段时间间隔内，通过对电压型逆变器的开关状态的线性组合，得到磁链矢量轨迹为圆形的PWM方式。SVPWM控制算法的思想是：运用定子磁链空间矢量跟踪的思想，在正弦波永磁同步电机内部空间产生旋转的圆形磁场，从而产生稳定的电磁转矩。

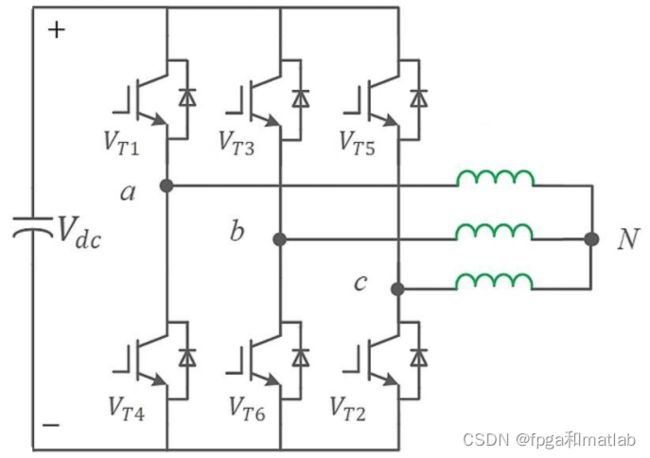
      三相逆变器对PMSM供电时，SVPWM技术产生的PWM波控制着三相逆变器的六个开关管的开通与关闭。逆变器结构如图１所示，逆变器由三个桥臂六个开关管组成，为避免短路，逆变器同一个桥臂上的两个电子开关交替导通。

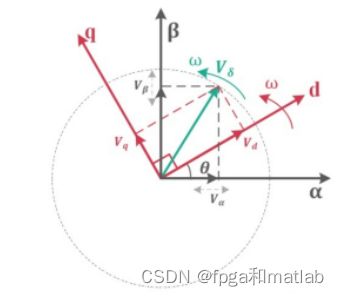
 1.1PARK变换

1.2CLARK变换

 

二、核心程序

 

function [sys,x0,str,ts] = func_N_calculation(t,x,u,flag)
%A=0;B=0;
%C=0;N=0;


global A B C N;
switch flag,
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
  case 1,
    sys=[];
  case 2,
    sys=[];
  case 3,
    sys=mdlOutputs(t,x,u,A,B,C,N);
  case 4,
    sys=[];
  case 9,
    sys=[];
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end


function [sys,x0,str,ts]=mdlInitializeSizes

sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 3;
sizes.NumOutputs     = 1;
sizes.NumInputs      = 2;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;   % at least one sample time is needed

sys = simsizes(sizes);
x0  = [0 0 0];
str = [];
ts  = [0 0];

%u(1)=Uafa;u(2)=Ubta
function sys=mdlOutputs(t,x,u,A,B,C,N)
x(1)=u(2);                         %x(1)=Ua
x(2)=1/2*(sqrt(3)*u(1)-u(2));      %x(2)=Ub
x(3)=1/2*(-sqrt(3)*u(1)-u(2));    %x(3)=Uc

if (x(1)>0);    %A
   A=1;
else
   A=0; 
end
if (x(2)>0);     %B
   B=1;
else
   B=0; 
end
if (x(3)>0);
   C=1;          %C
else
   C=0; 
end
N=4*C+2*B+A;   %N
sys=N;

function [sys,x0,str,ts] = func_T1T2_cal(t,x,u,flag)

switch flag,
    
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
  case 1,
    sys=[];
  case 2,
    sys=[];
  case 3,
    sys=mdlOutputs(t,x,u);
  case 4,
    sys=[];
  case 9,
    sys=[];
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end


function [sys,x0,str,ts]=mdlInitializeSizes

sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 2;
sizes.NumInputs      = 5;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;   % at least one sample time is needed

sys = simsizes(sizes);
x0  = [];
str = [];
ts  = [0 0];

%u(1)=N;u(2)=Uafa;u(3)=Ubta;u(4)=Udc;u(5)=Ts
function sys=mdlOutputs(t,x,u)
global T1 T2 Ts
Ts=u(5);
switch u(1)
    case 1
        T1=-1*u(2)+3^0.5/3*u(3);
        T2=1*u(2)+3^0.5/3*u(3);
    case 2
        T1=1*u(2)+3^0.5/3*u(3);
        T2=0*u(2)-2*3^0.5/3*u(3);
    case 3
        T1=1*u(2)-3^0.5/3*u(3);
        T2=2*3^0.5/3*u(3);
    case 4
        T1=-2*3^0.5/3*u(3);
        T2=-1*u(2)+3^0.5/3*u(3);
    case 5
        T1=2*3^0.5/3*u(3);
        T2=-1*u(2)-3^0.5/3*u(3);
    case 6
        T1=-1*u(2)-3^0.5/3*u(3);
        T2=1*u(2)-3^0.5/3*u(3);
end 
T1=T1*u(5)/u(4)/2*3;
T2=T2*u(5)/u(4)/2*3;

if (T1+T2<=Ts);
    sys(1)=T1;
    sys(2)=T2;   
else
    sys(1)=T1*Ts/(T1+T2);
    sys(2)=T2*Ts/(T1+T2);
end

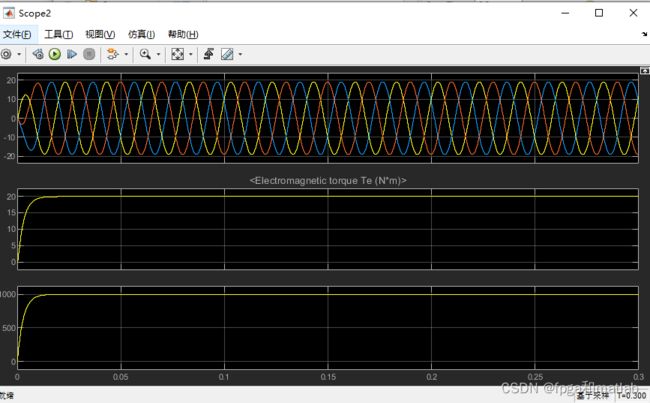
三、仿真测试结果

 A22-04