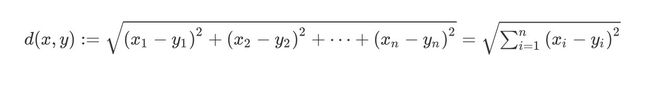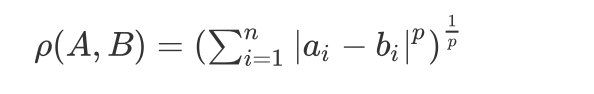机器学习-KNN算法
从KNN算法步入机器学习殿堂
本文中介绍的机器学习算法中的一种监督学习的算法:KNN算法,全称是K-Nearest Neighbor,中文称之为K近邻算法。
它是机器学习可以说是最简单的分类算法之一,同时也是最常用的分类算法之一。在接下来的内容中,将通过以下的几个方面的内容对该算法进行详细的讲解:
算法思想
思想
首先对KNN算法的思想进行简单的描述:
KNN算法是一个基本的分类和回归的算法,它是属于监督学习中分类方法的一种。其大致思想表述为:
- 给定一个训练集合M和一个测试对象n,其中该对象是由一个属性值和未知的类别标签组成的向量。
- 计算对象m和训练集中每个对象之间的距离(一般是欧式距离)或者相似度(一般是余弦相似度),确定最近邻的列表
- 将最近邻列表中数量占据最多的类别判给测试对象z。
- 一般来说,我们只选择训练样本中前K个最相似的数据,这便是k-近邻算法中k的出处。
用一句俗语来总结KNN算法的思想:物以类聚,人以群分
说明
- 所谓的监督学习和非监督学习,指的是训练数据是否有类别标签,如果有则是监督学习,否则是非监督学习
- 在监督学习中,输入变量和输出变量可以连续或者离散的。如果输入输出变量都是连续型变量,则称为回归问题(房价预测);如果输出是离散型变量,则称之为分类问题(判断患者是否属于患病)
- 在无监督学习中,数据是没有任何标签的,主要是各种聚类算法(以后学习)
算法步骤
KNN算法的步骤非常简单:
- 计算未知实例到所有已知实例的距离;
- 选择参数
K(下面会具体讲解K值的相关问题) - 根据多数表决(
Majority-Voting)规则,将未知实例归类为样本中最多数的类别
图解KNN算法
K值影响
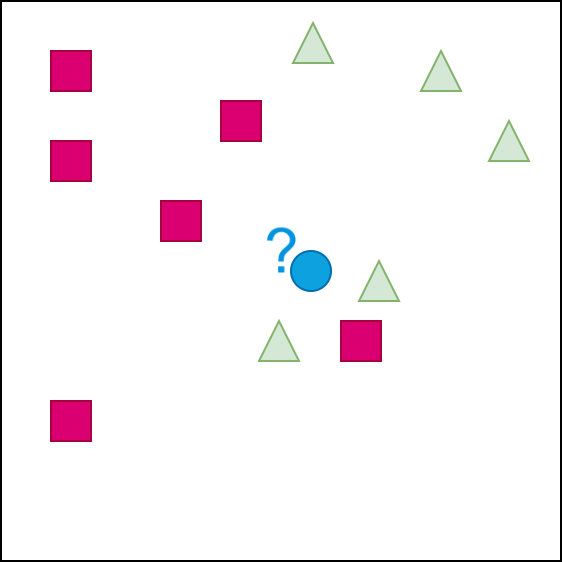
下面通过一组图形来解释下KNN算法的思想。我们的目的是:判断蓝色的点属于哪个类别
我们通过变化K的取值来进行判断。在该算法中K的取值一般是奇数,防止两个类别的个数相同,无法判断对象的类别
K=1、3、5、7…….
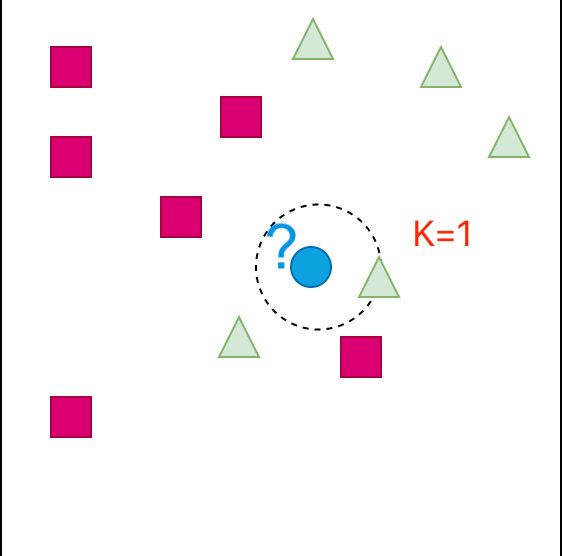
- 首先如果K=1:会是什么的情况?
根据图形判断:蓝色图形应该是属于三角形
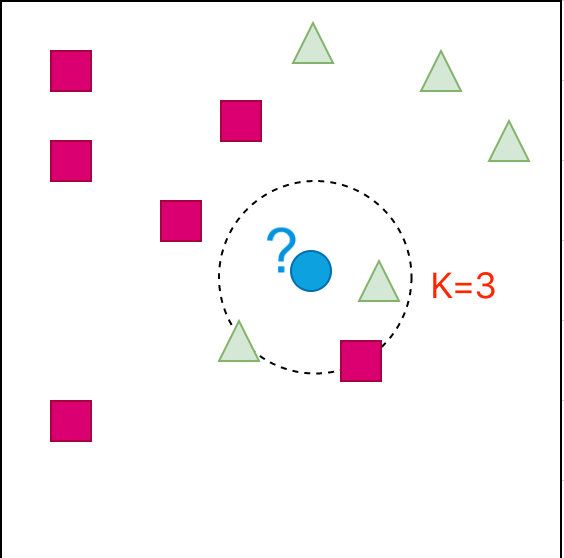
- K=3的情形
从图中可以看出来:蓝色部分还是属于三角形
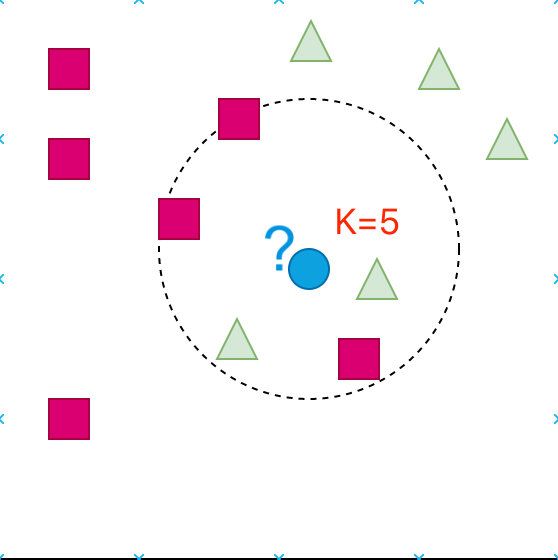
- K=5的情形:
此时我们观察到蓝色部分属于正方形了
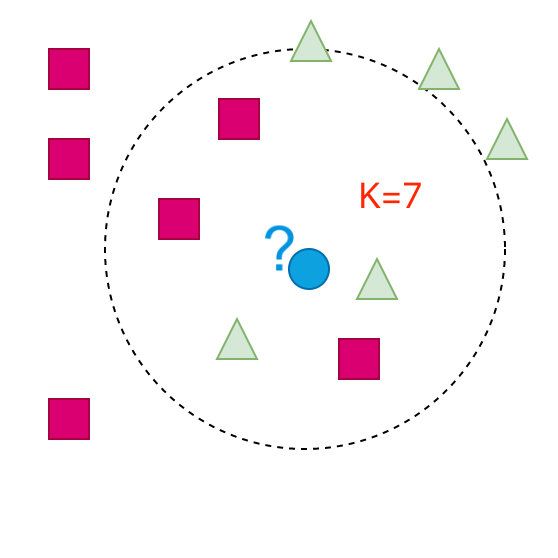
- K=7的情形:
这个时候蓝色部分又变成了三角形
小结
当K取值不同的时候,判别的结果是不同的。所以该算法中K值如何选择将非常重要,因为它会影响到我们最终的结果。
K值选取
交叉验证
上面的一系列图形中已经说明了该算法中K值对结果的影响。那么K值到底该如何选择呢?谜底揭晓:交叉验证
K值一般是通过交叉验证来确定的;经验规则来说,一般k是低于训练样本数的平方根
所谓交叉验证就是通过将原始数据按照一定的比例,比如6/4,拆分成训练数据集和测试数据集,K值从一个较小的值开始选取,逐渐增大,然后计算整个集合的方差,从而确定一个合适的K值。
经过使用交叉验证,我们会得到类似如下的图形,从图形中可以明显的:
- 当K先不断增大的时候,误差率会先进行降低。因为数据会包含更多的样本可以使用,从而分类效果会更好
- 当K=10的附近,出现误差率的变化,建议K=9或者11
- 当K不断增大的时候,误差率将会不断增加。此时,KNN算法将会变得没有意义。比如有50个样本,当K增加到45的时候,算法没有意义,几乎使用了全部样本数据,没有体现出最近邻的思想
K值过小
k值太小:容易受到噪声点的影响
- 用较小的邻域中的实例进行预测
- 近似误差减小,估计误差增大
- 预测结果对近邻的实例点非常敏感;如果近邻点恰好是噪声,预测出错
K值过大
k值太大:分类太多,太细,导致包含太多其他类别的点
- 用较大的邻域中的实例点进行预测
- 减少学习的估计误差,但是近似误差增大
- 与输入实例较远的点的训练实例也会起预测作用
- k值增大意味着整个模型变得简单
距离问题
常见距离
在上面的算法原理中提到,需要计算测试对象和训练集合中每个对象距离。在机器学习中,两个对象之间的距离包含:
常用的距离有以下几种:
- 欧式距离
- 曼哈顿距离
- 切比雪夫距离
- 闵可夫斯基距离
- 标准欧式距离
- 马氏距离
- 汉明距离
- 夹角余弦
- 杰卡德相似系数
在KNN算法中我们一般采用的是欧式距离(常用)或者曼哈顿距离
欧式距离
N维空间的距离:
d ( x , y ) : = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x, y):=\sqrt{\left(x_{1}-y_{1}\right)^{2}+\left(x_{2}-y_{2}\right)^{2}+\cdots+\left(x_{n}-y_{n}\right)^{2}}=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}} d(x,y):=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2=i=1∑n(xi−yi)2
当n=2时候,称之为欧式距离:
ρ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 , ∣ X ∣ = x 2 2 + y 2 2 \rho=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}},|X|=\sqrt{x_{2}^{2}+y_{2}^{2}} ρ=(x2−x1)2+(y2−y1)2,∣X∣=x22+y22
其中X称之为到原点的欧式距离
曼哈顿距离
曼哈顿距离是闵可夫斯基距离的一种特殊情形。闵可夫斯基距离指的是:
ρ ( A , B ) = ( ∑ i = 1 n ∣ a i − b i ∣ p ) 1 p \rho(A, B)=\left(\sum_{i=1}^{n}\left|a_{i}-b_{i}\right|^{p}\right)^{\frac{1}{p}} ρ(A,B)=(i=1∑n∣ai−bi∣p)p1
当p=2,变成欧式距离;
当p=1,变成曼哈顿距离;
当p区域无穷,变成切比雪夫距离;
算法优缺点
优点
- 简单易用,而且非常容易弄懂基本原理,
KNN算法可以说是机器算法中最简单易懂的算法。即使初学者没有太多的基础,相信也能明白它的原理。 - 算法是惰性的,模型训练时间快。
KNN算法没有明确的数据训练过程,或者说它根本不需要进行数据的训练,直接可以对测试对象进行判断。 - 适合用于多分类问题(对象具有多个标签)。
缺点
- 对计算机的内存要求高:因为它存储了整个训练数据,性能较低
- 算法的可解释差,对结果不能给出一定的解释规则
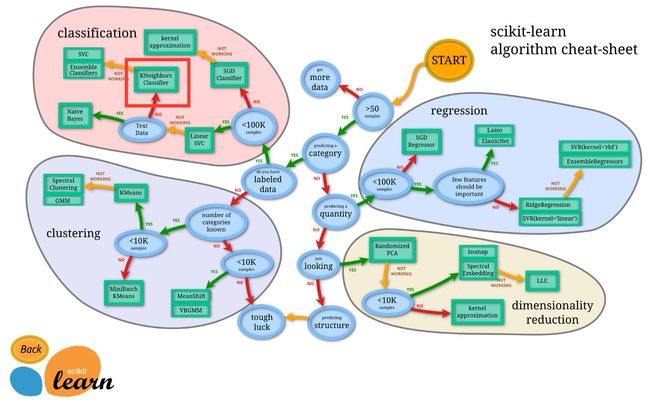
什么时候使用KNN算法?scikit-learn官方中的一张图给出了一个答案:
KNN算法实现
下面通过一个简单的算法来实现KNN算法,主要步骤为:
- 创建数据集合和标签
- 利用欧式距离,使用
KNN算法进行分类- 计算欧式距离
- 距离的排序(从大到小)
- 统计K个样本中出现次数多的,归属于该类别
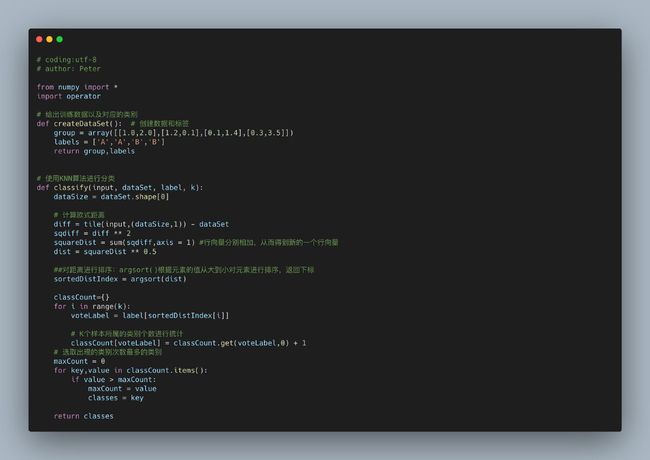
# coding:utf-8
# author: Peter
from numpy import *
import operator
# 给出训练数据以及对应的类别
def createDataSet(): # 创建数据和标签
group = array([[1.0,2.0],[1.2,0.1],[0.1,1.4],[0.3,3.5]])
labels = ['A','A','B','B']
return group,labels
# 使用KNN算法进行分类
def classify(input, dataSet, label, k):
dataSize = dataSet.shape[0]
# 计算欧式距离
diff = tile(input,(dataSize,1)) - dataSet
sqdiff = diff ** 2
squareDist = sum(sqdiff,axis = 1) #行向量分别相加,从而得到新的一个行向量
dist = squareDist ** 0.5
##对距离进行排序:argsort()根据元素的值从大到小对元素进行排序,返回下标
sortedDistIndex = argsort(dist)
classCount={}
for i in range(k):
voteLabel = label[sortedDistIndex[i]]
# K个样本所属的类别个数进行统计
classCount[voteLabel] = classCount.get(voteLabel,0) + 1
# 选取出现的类别次数最多的类别
maxCount = 0
for key,value in classCount.items():
if value > maxCount:
maxCount = value
classes = key
return classes