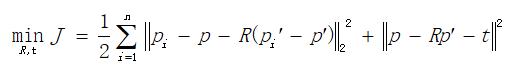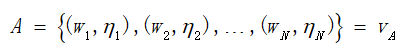基于ROS机器人的3D物体识别与三维重建(四)视觉SLAM基础(十四讲学习记录)
视觉SLAM基础理论
- 1 引言
- 2 视觉里程计
-
- 2.1 特征点法VO
-
- (1)对极几何与三角量测
- (2)PnP问题
- (3)ICP迭代最近点法
- 2.2 直接法VO
- 3 后端优化
-
- 3.1 BA与非线性优化
- 3.2 基于位姿图的优化
- 3.3 图优化与G2O
- 4 回环检测
-
- 4.1 回环检测介绍
- 4.2 词袋模型与字典
- 4.3 相似性
- 5 建立三维地图
-
- 4.1 Mapping介绍
- 4.2 RGB-D建图理论
-
- (1)点云地图
- (2)八叉树地图
- (3)纹理地图
- (4)TSDF地图
相关的代码资料:
https://github.com/Rayso777(后续会陆续整理上传)
视频:
1、ElasticFusion TUM数据集&buntu16.04+kinect2演示流程.
2、RTAB-MAP实时三维重建-Kinect2
3、RTAB-MAP三维重建-基于gazebo仿真
4、ORB-SLAM2室内稀疏三维重建-基于gazebo仿真
5、ORB-SLAM2室外三维重建-gezebo仿真
6、三维重建视频集锦-视觉SLAM
1 引言
机器人进行各种功能任务的基础便是物体识别和环境感知,在前面章节已经对物体识别进行了详细的探讨。本章开始,将对环境感知进行详细的介绍。
机器人的环境感知主要就是通过自身携带的传感器来获取环境信息,同时根据这些信息估计自身在环境的位置,这也就是SLAM(Simultaneous Localization and Mapping),即同时定位和建图技术。该技术是机器人后续路径规划、避障、交互等功能任务的基础。根据传感器的类型不同,可以分为激光SALM和视觉SLAM。由于本文的实验环境主要基于Kinect相机,所以也主要点视觉SLAM技术进行研究。
视觉SLAM技术最核心的内容便是通过一系列的的图片进行定位和建图,涉及数学几何方面的的大量知识,它已经发展多年,拥有了一个比较成熟的理论框架,如下图所示,通过传感器获取图像和IMU等信息,在VO中对两帧数据之间的位姿进行估计并构建局部地图,后端采用非线性优化或者EKF等方法对VO和回环检测的结果的优化构建更准确的的地图和位姿,回环检测用于识别机器人当前帧的图片与之前数据相似度,判断是否是同一位置,用于轨迹纠正优化,最后通过建图环节构建稀疏、半稠密、稠密等不同类型的地图用于机器人后续路径规划等功能任务。

会对VO、后端优化、回环检测、Mapping等四个环节进行介绍,以了解VSLAM技术的流程,以便对后续机器人三维重建奠定基础。
2 视觉里程计
视觉里程计主要的作用便是根据两幅图像估计相机的运动。VSALM可以根据视觉里程计的不同分为基于特征点和基于直接法的两大类,前者代表为PTAM和ORB-SLAM,后者有SVO何DSO等算法。因此,在该模块,我们将分为特征点VO和直接法VO两类进行研究。因为本文采用的三维重建算法基于特征点法,因此我们将对这一部分详细研究,对直接法仅简要介绍。
2.1 特征点法VO
特征点法视觉里程计主要基于特征点开展的,根据相邻两幅图像的匹配特征点,来估计相机的位姿R、t。在第三章物体识别中我们已经完成了ORB特征的提取和匹配,所以这里不再重新叙述。当我们获取了匹配好的特征点后,便可以根据匹配的图像对相机的运动进行估计。目前主流的方法可以分为用于二维到二维映射的对极几何和三角量测、用于二维到三维映射的PnP和用于三维到三维映射的ICP等方法。对极几何主要用于单目相机,ICP主要用于双目和RGB-D相机等可以获取深度的相机,而PnP用于知道空间点位置和在像素坐标系的坐标情况下求解相机位姿。下面对这三种情况分别进行介绍。
(1)对极几何与三角量测

上图中,p1和p2是一对匹配特征点,可以通过相机模型很容易求得空间坐标P在两幅图像中的像素坐标:
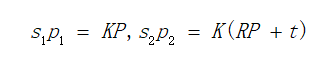
通过添加相机内参K的逆矩阵和t的反对称矩阵对上面两个式子进行变换,最终可以得到对极约束 :

其中E为本质矩阵,F为基础矩阵。对极约束中含有旋转和平移矩阵,因此只要求得E或者F便可以得到相机的位姿。
对E进行求解,主要使用八点法求解,设存在两个点满足对极约束,则:

采用八点法求解,共有八对匹配点,因此可以写成下面的形式,很容易便可对本质矩阵求解。

在得到本质矩阵E后对其进行奇异值分解,便可以得到相机的旋转矩阵R和平移矩阵t。最终我们会得到两个旋转矩阵和平移矩阵,两两组合会产生四种情况,如下所示,我们只需要筛选空间点在相机中俱有正的深度的解即可。

在求得相机的R、t后需要对空间点距离相机光心的距离进行估计,需要用到三角量测进行计算。如下:

经过上面公式的推导,可以看出,第二个公式只有s2一个变量,将对极几何求得的R、t带入式子便可求出s2,随即也可以求得s1。至此,我们已经求得了两幅图像之间相机的位姿变换和各自对应的空间点在像极坐标系的深度,也可进一步求出在相机坐标系的坐标。
(2)PnP问题
对极几何解决了已知两幅图像点对匹配求解相机位姿变换的问题,而接下来涉及的PnP则是解决已知空间的三维点和像素坐标系的二维点对应关系求解相机位姿的问题。
可以通过直接线性变换、P3P和非线性优化求解PnP,下面分别进行介绍。
1、直接线性变换DLT
定义包含旋转矩阵和平移矩阵的增广矩阵,则将空间点映射到二维平面上则有:

消去s可以得到:

令t1、t2和t3如下:

有:

T共有12个变量,而每个特征点提供了两个方程约束,因此只需要6个特征点便可以对增光矩阵求解。设有N个特征点,则有:

对于点数多的超定方程可以求解最小二乘解。另外,求解的3x4的矩阵,前三列并不是旋转变换矩阵R,因为R属于特殊正交群,满足正交关系。我们所求解的只是普通的矩阵,因此我们需要对R进行重新的近似。可以通过QR分解进行对R、t的求解。
2、P3P求解
以上便是直接法(DLT),需要至少6个点才可以求解,下面介绍P3P的方法,它只需要3个点对便可以求解。
该方法需要知道空间三个点在世界坐标系的坐标和成像平面的坐标,然后通过相似三角形、正余弦定理和方程组求解。
3、非线性优化
DLT和P3P都是线性求解的方法,我们也可以通过将PnP的数学模型转换为李代数的最小二乘问题来用非线性的方法求解。将相机运动R、t通过指数映射变为对应的李代数,空间坐标系和像素坐标系对应点可通过下式表示:

通过重投影误差构建最小二乘问题如下,则可以通过高斯牛顿法和LM法进行梯度迭代求解。

(3)ICP迭代最近点法
当已知空间中两帧图像匹配点对应的三维点时,我们可以采用最近迭代法进行三维点到三维点的位姿估计。ICP问题的求解方法主要有SVD和非线性优化。
1、SVD线性求解
假设两幅图像有N对由特征匹配好的3D空间点,则我们可以通过刚体变换的关系构建基于重投影误差的最小二乘问题。

由上方式子的结构特征看出,通过对左侧求R,再将其带入右侧求t,便可以求解出相机的运动。因此,ICP的流程可以分为以下的步骤:
该方法的难点也就在R的求解上,只要求出R,t也就自然而然可以求出。通过对重投影误差模型的推导,可以得到下方公式:

通过对上式进行SVD推导,可以得到旋转矩阵R,平移矩阵t亦可随即求出。
2 、非线性优化
除了使用SVD的方法对ICP问题求解外,还可以使用李代数代替旋转变换矩阵,使用非线性优化的方式梯度迭代进行求解,主要通过LM和高斯牛顿法等。

一般,深度相机都有一定的测距范围,超过这个范围或者由于光线的影响会导致深度获取不到,因此在使用深度相机ICP估计相机运动的过程中,存在3D空间点深度丢失的情况。因此,结合对极几何和PnP一起进行优化便十分有必要,这样可以得到较好的结果。
2.2 直接法VO
基于特征点法的视觉里程计虽然可以很好的估计相机位姿,但在特征点提取和匹配的计算过程中会消耗大量时间。而直接法不需要在特征点上消耗时间,很好的提高了运行效率。直接法是基于光度一致性假设,不需要计算关键点和描述子,直接根据图像之间灰度的大小来估计相机的位姿运动。同特征点法需要构建重投影误差的数学模型一样,直接法需要构建光度误差模型。

由图所示原理可得以下公式:

两幅图像对应点的光度误差为:
![]()
因此对该光度误差的二范数进行优化即可求得相机运动。
![]()
3 后端优化
VO主要估计相机的运动和特征点的空间位置,可以得到一段时间内的相机运动轨迹和局部的地图。而随着长时间的运行,由于相机制造本身的误差、光照和环境等因素的影响,轨迹和地图会发生偏移。在VO的基础上,构建长时间的大规模的轨迹和地图优化便是后端的主要内容。
后端优化可以分为卡尔曼滤波和非线性优化两大类方法。近些年的相关研究工作已经证明非线性优化的方法明显的优于卡尔曼滤波,并且本文采用的三维重建算法也基于非线性优化的后端,因此在这一环节,我们将主要介绍非线性优化。
3.1 BA与非线性优化
相机的成像过程可由下方的流程图进行表示:

这个过程就是相机的观测方程,可以由下方的h函数进行简化表示:
![]()
式中x代表相机位姿,主要用李代数进行表示,y代表空间点,z是像素坐标系的坐标。观测误差可以表示为:
![]()
我们将观测的所有点列进该式,可以写为:

使用梯度方向迭代的方法不断对相机位姿和路标定进行捆绑调整,这也是BA(Bundle Adjustment)的过程。将待优化的变量定义在一个一维数组变量中,包括位姿和路标。
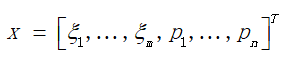
当给定扰动后,目标函数为:

其中,F代表对相机位姿求偏导,E为对空间点求偏导。变为矩阵形式后为:

我们设定雅克比矩阵为:

又由于高斯牛顿法和LM方法最终的增量扰动可统一为:
![]()
![]()
为待求解矩阵,用于梯度下降方向的选择,H矩阵如下式4.3.9所示,该矩阵包括了待优化的所有位姿和路标,矩阵的维数十分大,直接求逆的方法来求增量显然不现实,所有我们会利用H矩阵特有的稀疏特性进行求解。

3.2 基于位姿图的优化
BA是通过观测方程和运动方程共同建立的模型进行优化,虽然可以解决大规模的优化问题。但是随时间的增长,路标点和位姿会越来越多,需要优化的变量也将呈指数级别增长,这对视觉SLAM的实时性带来了挑战。而采用位姿图(Pose Graph)的优化方式可以较好的解决这些问题。
上图对比了BA与位姿图。观测方程中的路标点在长时间的观测优化后会逐步地趋向稳定,而此时我们仍然对这些路标定进行优化并不能提升太多精度,反而浪费运算时间。因此我们可以将路标定当做定值,舍弃对这些变量,而只针对位姿进行优化,这样便可以极大降低计算量提高运行效率。
3.3 图优化与G2O
视觉SLAM的后端有两个主要的非线性优化库 Ceres 和 G2O 。Ceres 是谷歌开发的一个用于最小二乘问题的库,该库使用十分方便,输入问题的描述模型、设置求解方式和参数即可。
G2O库同Ceres相比,用途范围更广。该库是基于图优化理论开发的,图是由顶点和边组成,顶点代表需要优化的变量,边代表误差项,对于一个后端优化问题,我们只需要构造顶点和边输入、并设置参数选项就可以进行后端的求解。如下图所示:

通过 Ceres 和 G2O 两个非线性优化的两个主要工具库,我们可以省去中间的大量重复编程环节,只需要构建优化的目标函数便可以轻松的完成优化,一定程度上很大提高了开发效率。
4 回环检测
4.1 回环检测介绍
VO是对相邻两帧图像处理估计相机的运动变换矩阵,而当前帧的运动估计误差则会累积到后面的估计当中,因此对机器人的运动轨迹估计则产生了漂移。回环检测的加入便可以很好的解决这个问题。如下图所示,机器人所估计的运动轨迹和构建的二维地图会随着时间发生较大偏移,通过回环检测识别机器人之前到过的地方的场景信息,将位姿信息和路标代入后端优化中对之前的所有数据进行优化纠正。

回环检测对长时间下的大规模位姿轨迹和地图的精确性保证具有重要意义,同时,在VO构建局部地图过程中会存在跟踪特征丢失的情况,而使用回环检测便可以进行重定位。
4.2 词袋模型与字典
回环检测最重要的便是当前帧数据同之前的历史图像之间的相似度计算,而词袋模型(Bag-of-Words)便是在该环节我们常用的方法。词袋模型核心的概念便是根据两幅图像的特征进行相似度计算,比如一幅图像中有桌子和椅子两个特征,而在另外一幅图像中也发现了这两个特征,我们便可以认为这两张图像相似。而这些特征便是word,组合起来便是字典。
我们可以对一幅图像用向量进行表示,比如一幅图像有两张桌子,一张椅子,则可以表示为:
![]()
因此可用[2,1]表示图像I,如果系数为0则表示没有出现该特征。此处的特征并非特征点,而是一堆特征点的聚合。字典是由一系列的单词构建的,单词是图像中一群类似的特征点的集合,所以构建字典也可看做无监督学习过程中的聚类问题。在一幅图像中提取ORB、SIFT等特征点后,使用 K-means 算法进行聚类,流程如下图所示:

但这种算法也存在缺点,需要制定所需要分类的类别数目,并且在查找匹配的过程中时间复杂度比较高。因此通常会结合KD-Tree对K-meas进行优化。

假设一幅图像里所有的特征点包含在根节点中,然后使用k-means对根节点的所有特征点进行聚类,结果为图示的第一层子节点,以此类推,再对第一层的子节点各自使用k-means,最后得到叶子节点,也就是单词。这种 kd-tree 的存储结构可以极大的减少我们匹配查找的时间。
4.3 相似性
通过 BoW构建的字典,可以将当前帧的图像与历史图像进行匹配,但单纯的判断特征的存在与否会造成大量的误匹配。比如室内的墙面背景会在很多图像中出现,如果只是单纯依据墙面便会造成匹配的误判,因此我们为每个单词加上权重进行进一步优化。引入了TF-IDF的概念,其中TF是指出现频率较高的词区分度也比较高(在图像中),出现频率低的词对图像判别时区分度也高(在字典中)。如果有N个特征点,某个单词数目有n个,则有:

5 建立三维地图
4.1 Mapping介绍
SLAM的两个主要目标分别是定位和建图。在VO、后端以及回环检测中,我们对相机估计的位姿和运动轨迹进行了详细的探讨,并且在估计相机运动的过程中构建了位于世界坐标系下的三维路标点,这些路标点也可认为是地图。
对于机器人而言,视觉SLAM是一种底层地、为上层应用功能服务的技术。针对机器人所需的而不同功能,我们重建的地图种类也会有所不同。如果机器人只需要自己在环境中的位置,那么稀疏的特征点地图便可以满足该功能。并且对于虚拟现实和增强现实稀疏地图完全可以满足要求。但如果机器人需要具备导航、避障、自动路径规划等功能,那么稀疏的地图便显然捉襟见肘了。在这种情况下,我们便需要通过视觉SLAM技术构建稠密的地图,以便为机器人的上层应用功能提供环境信息。
基于视觉SLAM技术的三维重建中,根据相机类型的不同可分为单目、双目和深度相机重建。前两种统称为立体视觉重建,但前两种在获取深度信息上比较麻烦,比如单目稠密重建过程中要进行对极几何、三角量测、极线搜索和块匹配等,其算法的运行效率远没有直接采用 RGBD 相机直接获取深度进行重建效率高。但单、双目相机在室外的重建效果上比RGBD相机要好很多,因此也仍是研究的热点。由于本文主要对室内场景进行重建, 并且由于实验条件的限制,接下来主要对RGBD深度相机的重建进行探讨。
4.2 RGB-D建图理论
使用深度相机进行建图非常容易,它省去了单目相机建图过程中对距离的估计计算,降低了建图的难度并提高了建图的效率。地图的种类也很繁多,主要有点云地图、八叉树地图、纹理地图、TSDF地图等。
(1)点云地图
在各种地图中,点云地图是最为简单的一种,只需要将RGB-D相机获取的彩色图和深度图配准,便可得到相机坐标系下的点云,再将其结合相机的位姿转换到世界坐标系,便可得到点云地图。点云数据包括 RGB色彩信息和 XYZ 坐标信息。在第二章通过点云拼接的实验完成了点云地图的构架,并通过ROS实现了实时的获取点云。
但是这种稠密的点云地图在机器人进行定位过程中会消耗大量的资源,很难实现实时运行,因此我们大都采用基于特征点的点云点图,如下图所示:

特征点地图中的点为相机可识别的路标,机器人在运行过程中对路标识别便可估计自身的位姿了,可以通过人为构建机器人运行轨迹,让机器人自动规划路径移动。
(2)八叉树地图
点云地图存储的点云数量很大,这么多的空间点对计算机的的性能要求很高,而特征点地图虽然稀疏,但不能完整表达环境障碍物信息。八叉树地图却可以很好解决这些问题。

如上图所示,八叉树地图是用一个立方体来表示一定体积的空间,该立方体也代表根节点,不断的进行八等分直至叶子结点。当空间某处的中间节点没有物体占据时,我们对此节点便不用展开,当某个节点被占据便不断八等分。因此使用八叉树地图会极大的节省空间。我们一般使用1和0代表该空间被占据与否。对于机器人探索未知环境而言,存在未知的情况,因此我们可以采用0~1之间的概率方式进行表述,设定初值为0.5,不断观测到有物体则增加概率,若没有物体则降低概率。
(3)纹理地图
有时候在对未知环境探测中还需要得知细节的纹理信息,像救灾勘测机器人等,这时候需在点云的基础上构建面片网格等。
(4)TSDF地图
TSDF又叫做截断符号距离函数,该方法与八叉树地图的构建有些类似,不过该方法是直接将一个立体空间进行栅格化等分好,而八叉树地图则会将空白节点停着等分。该方法构建地图的核心内涵是正数代表在某个面的前方,负数代表在该面的后方,而0则是在面上。为了限制太远的地方,统一设为1。下面是一个二维的TSDF图,三维的立体图可类推。著名的KinectFusion三维重建算法便是在该基础上设计的。

上述内容介绍了通过深度相机可以构建的四类主要的地图,他们是通过地图数据的表达方式进行划分的。同时,我们也可以从地图的稀疏性上对其进行划分,可以分为稀疏地图和稠密地图。这也是目前通过视觉SLAM进行实时重建的两个主要研究方向。
基于稀疏特征点的三维重建和基于纹理与TSDF的稠密重建目前已经成为科研工作者研究的热点,对实际的技术应用具有重要意义,因此本文将针对这两种地图进行主要研究。
下篇博客节介绍ORB-SLAM2与RTAB-MAP三维重建