小波散射网络初级探索

自深度学习兴起后，深层网路对图像进行特征学习，将低层次的基础特征聚合成更高级的语义特征，取得突出的识别效果，在图像识别、分割及目标检测三大领域得到了众多应用。深度学习算法基本上是由多个网络层搭建，每个网络层可获得图像的一种特征表示，再将特征进行线性、非线性组合，随着网络层的深度增加，特征由基本浅层特征（比如角度、像素位置等）逐步转化为具有高层语义的高级特征，最终形成低维度且具有高识别度的特征表达。鉴于这类算法中特征提取器的参数主要是根据训练样本不断训练、反馈式地调整，因此该类型的算法有个共同的缺点就是需要大量的训练样本及其对应的标签，而且目前对网络的特性和具体配置 （包括网络需要多少层，为什么要使用多层，需要多少个内部和输出神经元，又如何优化滤波器和非线性操作）尚没有统一的结论。而且，为了对抗掉图像平移、旋转、形变等存在的一些基本变化，所研究的网络提取到的特征应该具备平移、旋转不变性、形稳定性等基本特性。此外，网络的设计理念也应该具备一定的理论依据。

2012 年，法国工程学院院士Mallat 教授（我崇拜的学者，还有Meyer教授，阿贝尔奖获得者，还有Daubechies教授，有幸和她见过一次）深受深度学习结构框架思想的启发，提出了基于小波变换的小波散射变换，并以此构造了小波散射卷积网络。小波散射卷积网络的结构类似于CNN，不同的是其滤波器是预先确定好的小波滤波器，小波滤波器的参数不需要通过训练样本学习得到，其网络是非反馈式的。信号通过计算半离散小波变换，再通过非线性取模操作，得到的信号特征表达具有平移不变性、形变稳定性等优良特性，正好满足机器学习中对特征提取器的基本要求。此外，这些基本性质在数学上得到了严格的理论证明，弥补了CNN缺乏理论支撑的不足。经过大量试验，小波散射网络在手写体识别、纹理和音频分类任务中取得了突出的分类效果，尤其在小样本的情况下，相较于CNN获得了更小的分类错误率，因此小波散射卷积网络具有一定的优势以及研究意义。

此外，再简单介绍一下小波散射网络的发展历程。自 21 世纪起，小波理论的奠基人之一 Mallat 等便开始对卷积神经网络的数学分析与研究。2012 年，Mallat以CNN结构为基础，提出小波散射变换，并以此为基础构造出了小波散射卷积网络。小波散射变换将原始信号通过预先设定好的小波滤波器和取模的非线性操作，得到的结果作为对该信号所提取的特征，经过理论验证，小波散射卷积网络具有平移、旋转不变性、形变稳定性等基本特性，CNN相比，小波散射网络由于采用了固定的小波核，无需反馈过程，因此摆脱了对训练样本的依赖性。自 2012年后，小波散射网络在国外就受到各界的广泛关注并且开始逐步在各个领域加以应用，其应用范围涉及信号处理领域的时频分析、计算机视觉方面的各种识别问题，例如纹理识别等，甚至拓展到生命科学领域，如生物神经信号的分析、检测与预测等方面。2013年，Mallat 将小波散射网络应用到语音时频分析领域，将提取出的语音信号特征直接用来分类，实现了在音频信号分类方面的应用。同年 8 月，Mallat 又将小波散射卷积网络拓展到二维信号分析中，将小波散射卷积网络作为特征提取器，提取出的特征直接用 SVM (高斯核) 和 PCA 进行分类，取得了手写数字和纹理辨别方面的最新分类结果，特别是在具有标签的样本数较小的情况下，与CNN相比，该网络获得了更低的分类错误率。2016 年，Mallat 对小波散射网络进行综述，系统地介绍该网络的核心思想、应用领域及发展现状。同年 6 月，瑞士应用数学家 Wiatowski 从理论上验证了几种具有不同的下采样率和非线性操作的散射网络，进一步阐述了Mallat 的小波散射卷积网络研究成果对应用数学领域的思想启发。2018年，Wiatowski 对小波散射变换做了进一步的深入研究，主要考察其基本的数学性质，对此进行了严密的数学推导和理论证明，进一步证明小波散射变换在特征提取方面的优越性，并将其理论进行了推广，得到泛化后的小波散射框架即一般化的散射卷积网络的框架与结构。2019 年，Li将 Mallat的研究成果进一步拓展，将时频 Gabor 变换与小波散射卷积网络的网络框架相结合，提出了时频散射变换，并构造出了时频散射卷积网络，在高光谱识别等方面也取得了不错的成果。综上所述，小波散射卷积网络凭借其理论较为完备，所需具有标签的样本少等优势，在艺术鉴赏、天文学、量子化学、生物医学、雷达目标识别与探测等方面的应用遍地开花，而且取得了突出的应用效果，引起了国内外研究学者的广泛关注。妈的，越来越论文化了。

小波散射的理论方面可自行查看众多学术论文[1-4]，与深度学习一样，是分阶段（分层）处理数据的，一个阶段的输出成为下一个阶段的输入，每个阶段由三个操作组成

具体地

接下来开始步入正题。这篇文章主要讲解如何使用小波散射方法进行图像分类。对于分类问题，将数据映射到某个“表示域”中通常很有用，该“表示域”弱化不相关的信息，同时保留每个类别的区分属性。而小波散射方法构造了对平移和微小形变不敏感的图像的低方差表示。由于图像中的平移和小变形并不会影响其类别，因此小波散射变换系数提供了可以构建稳健分类模型的特征。小波散射的工作原理是对图像进行一系列小波变换、非线性和平均等级联操作。这种深度特征提取的结果是：在小波散射变换表示中，同一类别的图像彼此靠得更近，而不同类别的图像则相距更远。虽然小波散射变换与深度卷积神经网络在架构上有许多相似之处，包括卷积算子、非线性和平均，但小波散射变换中的滤波器是预先定义且固定的。

数字图像

本文使用的数据集包含10000张从0到9的数字合成图像，每个数字图像为 28×28 像素。数据集的每个类别包含相同数量的图像。

从数据集中随机选择并绘制 20 张图像

figure
numImages = 10000;
rng(100);
perm = randperm(numImages,20);
for np = 1:20
    subplot(4,5,np);
    imshow(Imds.Files{perm(np)});
end

可以看到数字8表现出相当大的可变性，样本中的其他重复数字也是如此，这与人们的自然笔迹一致，其中同一个人的笔迹在平移、旋转和微小形变方面都存在显着差异。因此希望使用小波散射建立对平移和微小形变不敏感的图像的低方差表示。

小波图像散射特征提取

图像大小为 28×28。因此创建一个小波图像散射框架并将InvarianceScale设置为图像的大小。小波散射滤波器组的旋转数NumRotations设置为8。然后通过tall数组接口使用MATLAB的并行处理能力。

if isempty(gcp)
    parpool;
end

为了便于重现，设置随机数生成器。并打乱imageDatastore中的文件，将 10000张图像分成两组，一组用于训练，一组用于测试。 将80%的数据分配给训练集，并保留剩余的2000张图像进行测试。 从训练和测试数据集中创建tall 数组。并从小波散射变换系数创建特征向量（获取小波散射变换特征矩阵的对数以及沿每个图像的行和列维度的平均值），由此得到一个 217×1 的特征向量。

rng(10);
Imds = shuffle(Imds);
[trainImds,testImds] = splitEachLabel(Imds,0.8);
Ttrain = tall(trainImds);
Ttest = tall(testImds);
trainfeatures = cellfun(@(x) WaveScat (sf,x),Ttrain,'UniformOutput',false);
testfeatures = cellfun(@(x) WaveScat (sf,x),Ttest,'UniformOutput',false);

连接所有训练和测试特征

Trainf = gather(trainfeatures);

trainfeatures = cat(2,Trainf{:});
Testf = gather(testfeatures);

testfeatures = cat(2,Testf{:});

前面的代码生成了两个矩阵，其行维数为 217，列维数分别等于训练集和测试集中的图像数量，因此每一列是其对应图像的特征向量。原始图像包含784个特征，小波散射系数表示每个图像的大小大约减少了 4 倍。

PCA 模型和预测

基于每个类别的小波散射特征向量的主成分构造一个简单的分类器，通过在每个测试特征向量的主成分与训练集之间找到最接近的匹配（最佳投影）。

model = PCA (trainfeatures,30,trainImds.Labels);
predlabels = PCAClassifier(testfeatures,model);

在构建模型并对测试集进行分类后，计算测试集分类的准确率

accuracy = sum(testImds.Labels == predlabels)./numel(testImds.Labels)*100

测试数据的分类准确率达到了99.6%，再看一下混淆矩阵。

此外，训练一个简单的卷积神经网络进行对比。构建的CNN包含一个卷积层，卷积层包括20 个5×5滤波器，步幅为 1×1，其后紧接、Relu激活函数层和最大池化层。最后使用全连接层，并使用softmax 将全连接层的输出归一化为概率。 损失函数使用交叉熵损失函数。

imageSize = [28 28 1];
layers = [ ...
    imageInputLayer([28 28 1])
    convolution2dLayer(5,20)
    reluLayer
    maxPooling2dLayer(2,'Stride',2)
    fullyConnectedLayer(10)
    softmaxLayer
classificationLayer];

使用带有动量和学习率为0.0001的随机梯度下降算法进行训练。最大epoch数设置为20，本文不用GPU，将 ExecutionEnvironment 设置为“cpu”

options = trainingOptions('sgdm', ...
    'MaxEpochs',20,...
    'InitialLearnRate',1e-4, ...
    'Verbose',false, ...
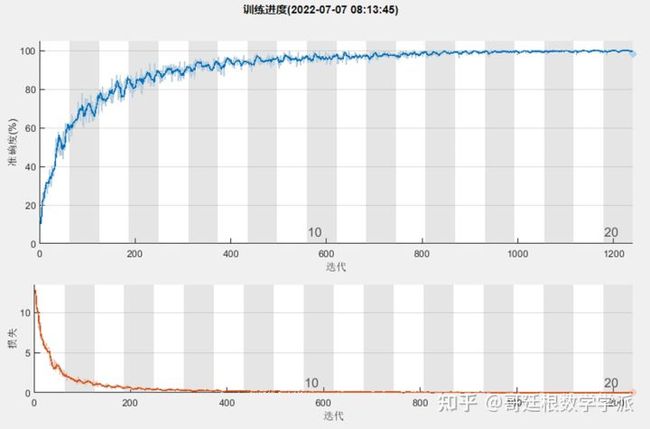
'Plots','training-progress','ExecutionEnvironment','cpu');。

训练网络

reset(trainImds);
reset(testImds);
net = trainNetwork(trainImds,layers,options);

训练结束时，CNN在训练集上的表现接近100%，然后对测试集进行测试

YPred = classify(net,testImds,'ExecutionEnvironment','cpu');
DCNNaccuracy = sum(YPred == testImds.Labels)/numel(YPred)*100

DCNNaccuracy = 95.1000

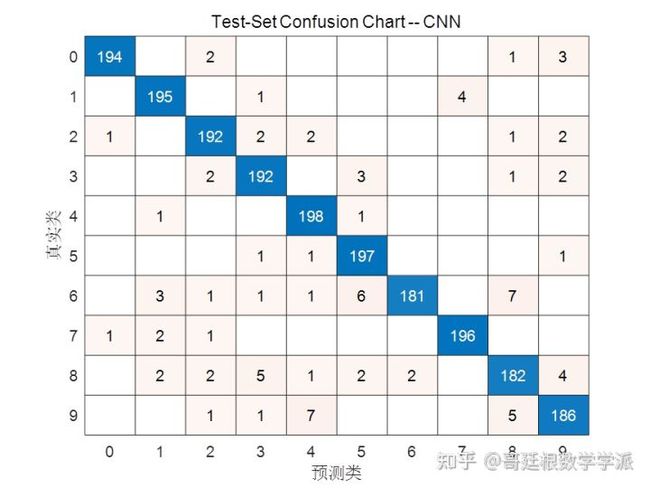
看一下混淆矩阵

小波散射网络在很多小数据集是表现的都很好。接下来将进一步研究基于小波散射网络的EEG信号识别和轴承故障诊断。

[1]Mallat S. Group invariant scattering[J]. Communications on Pure and Applied Mathematics, 2012, 65(10):1331-1398.

[2]Bruna J and Mallat S. Invariant scattering convolution networks[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(8):1872-1886.

[3]Talmon R, Mallat S, Zaveri H, and Coifman R. Manifold learning for latent variable inference in dynamical systems[J]. IEEE Transcations on Signal Processing, 2015,63(15):3843-3856.

[4]And´en J and Mallat S. Deep scattering spectrum[J]. IEEE Transactions on Signal Processing, 2014, 62(16):4114-4128.