数据挖掘：降低汽油精制过程中的辛烷值损失模型(一)

目录

一、背景

二、目标

三、问题

四、数据预处理

4.1 先开始285数据的处理： 

4.2 附件313数据的处理：

 4.3附件一的处理：

 4.4 拉以达准则

 4.5 缺失值的处理

---

题目文件：

链接: https://pan.baidu.com/s/1nuLPVPcZ7Ess8HCpbtC75Q 提取码: t9s7 

一、背景

汽油是小型车辆的主要燃料，汽油燃烧产生的尾气排放对大气环境有重要影响。为此，世界各国都制定了日益严格的汽油质量标准（见下表）。汽油清洁化重点是降低汽油中的硫、烯烃含量，同时尽量保持其辛烷值。

欧盟和我国车用汽油主要规格

车用汽油标准	辛烷值	硫含量/(μg/g) ≯	苯含量/% ≯	芳烃含量/% ≯		烯烃含量/% ≯
国Ⅲ（2010年）	90-97	150	1	40		30
国Ⅳ（2014年）	90-97	50	1	40		28
国Ⅴ（2017年）	89-95	10	1	40		24
国Ⅵ-A（2019年）	89-95	10	0.8	35		18
国Ⅵ-B（2023年）	89-95	10	0.8	35		15
欧Ⅴ（2009年）	95	10	1	35		18
欧VI（2013年）	95	10	1	35		18
世界燃油规范（Ⅴ类汽油）	95	10	1	35		10

注: μg/g是一个浓度单位，也有用mg/kg或ppm表示的（以下同）

我国原油对外依存度超过70%，且大部分是中东地区的含硫和高硫原油。原油中的重油通常占比40-60%，这部分重油（以硫为代表的杂质含量也高）难以直接利用。为了有效利用重油资源，我国大力发展了以催化裂化为核心的重油轻质化工艺技术，将重油转化为汽油、柴油和低碳烯烃，超过70%的汽油是由催化裂化生产得到，因此成品汽油中95%以上的硫和烯烃来自催化裂化汽油。故必须对催化裂化汽油进行精制处理，以满足对汽油质量要求。

辛烷值（以RON表示）是反映汽油燃烧性能的最重要指标，并作为汽油的商品牌号（例如89#、92#、95#）。现有技术在对催化裂化汽油进行脱硫和降烯烃过程中，普遍降低了汽油辛烷值。辛烷值每降低1个单位，相当于损失约150元/吨。以一个100万吨/年催化裂化汽油精制装置为例，若能降低RON损失0.3个单位，其经济效益将达到四千五百万元。

化工过程的建模一般是通过数据关联或机理建模的方法来实现的，取得了一定的成果。但是由于炼油工艺过程的复杂性以及设备的多样性，它们的操作变量（控制变量）之间具有高度非线性和相互强耦联的关系，而且传统的数据关联模型中变量相对较少、机理建模对原料的分析要求较高，对过程优化的响应不及时，所以效果并不理想。

某石化企业的催化裂化汽油精制脱硫装置运行4年，积累了大量历史数据，其汽油产品辛烷值损失平均为1.37个单位，而同类装置的最小损失值只有0.6个单位。故有较大的优化空间。请参赛研究生探索利用数据挖掘技术来解决化工过程建模问题。

二、目标

依据从催化裂化汽油精制装置采集的325个数据样本（每个数据样本都有354个操作变量），通过数据挖掘技术来建立汽油辛烷值（RON）损失的预测模型，并给出每个样本的优化操作条件，在保证汽油产品脱硫效果（欧六和国六标准均为不大于10μg/g，但为了给企业装置操作留有空间，本次建模要求产品硫含量不大于5μg/g）的前提下，尽量降低汽油辛烷值损失在30%以上。

三、问题

1. 数据处理：请参考近4年的工业数据(见附件一“325个数据样本数据.xlsx”)的预处理结果，依“样本确定方法”（附件二）对285号和313号数据样本进行预处理（原始数据见附件三“285号和313号样本原始数据.xlsx”）并将处理后的数据分别加入到附件一中相应的样本号中，供下面研究使用。

2. 寻找建模主要变量：

由于催化裂化汽油精制过程是连续的，虽然操作变量每3 分钟就采样一次，但辛烷值（因变量）的测量比较麻烦，一周仅2次无法对应。但根据实际情况可以认为辛烷值的测量值是测量时刻前两小时内操作变量的综合效果，因此预处理中取操作变量两小时内的平均值与辛烷值的测量值对应。这样产生了325个样本（见附件一）。

建立降低辛烷值损失模型涉及包括7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质等变量以及另外354个操作变量（共计367个变量），工程技术应用中经常使用先降维后建模的方法，这有利于忽略次要因素，发现并分析影响模型的主要变量与因素。因此，请你们根据提供的325个样本数据（见附件一），通过降维的方法从367个操作变量中筛选出建模主要变量，使之尽可能具有代表性、独立性（为了工程应用方便，建议降维后的主要变量在30个以下），并请详细说明建模主要变量的筛选过程及其合理性。（提示：请考虑将原料的辛烷值作为建模变量之一）。

3. 建立辛烷值（RON）损失预测模型：采用上述样本和建模主要变量，通过数据挖掘技术建立辛烷值（RON）损失预测模型，并进行模型验证。

4. 主要变量操作方案的优化：要求在保证产品硫含量不大于5μg/g的前提下，利用你们的模型获得325个数据样本(见附件四“325个数据样本数据.xlsx”)中，辛烷值（RON）损失降幅大于30%的样本对应的主要变量优化后的操作条件（优化过程中原料、待生吸附剂、再生吸附剂的性质保持不变，以它们在样本中的数据为准）。

5. 模型的可视化展示：工业装置为了平稳生产，优化后的主要操作变量（即：问题2中的主要变量）往往只能逐步调整到位，请你们对133号样本（原料性质、待生吸附剂和再生吸附剂的性质数据保持不变，以样本中的数据为准），以图形展示其主要操作变量优化调整过程中对应的汽油辛烷值和硫含量的变化轨迹。（各主要操作变量每次允许调整幅度值Δ见附件四“354个操作变量信息.xlsx”）。

四、数据预处理

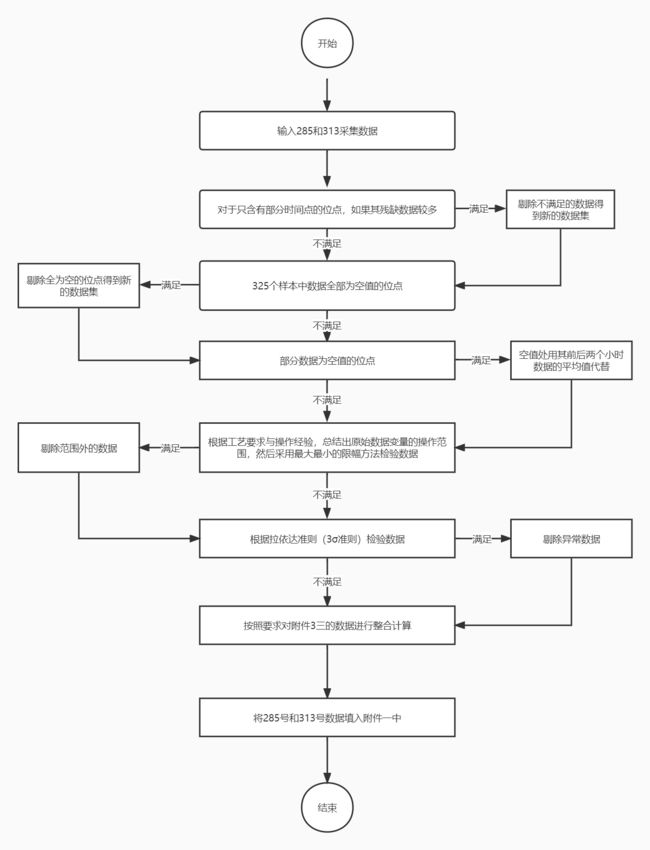
数据处理方法如下：

（1）对于只含有部分时间点的位点，如果其残缺数据较多，无法补充，将此类位点删除；

（2）删除325个样本中数据全部为空值的位点；

（3）对于部分数据为空值的位点，空值处用其前后两个小时数据的平均值代替；

（4）根据工艺要求与操作经验，总结出原始数据变量的操作范围，然后采用最大最小的限幅方法剔除一部分不在此范围的样本；

（5）根据拉依达准则（3σ准则）去除异常值。

图源于： http://t.csdn.cn/Ok3d1

4.1 先开始285数据的处理： 

import numpy as np
import pandas as pd
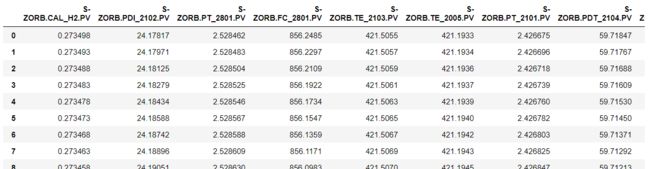
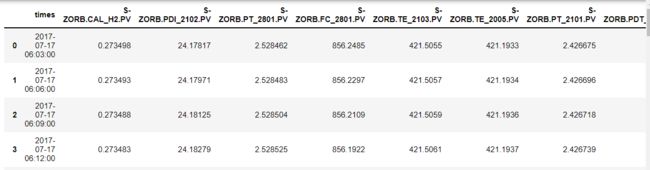
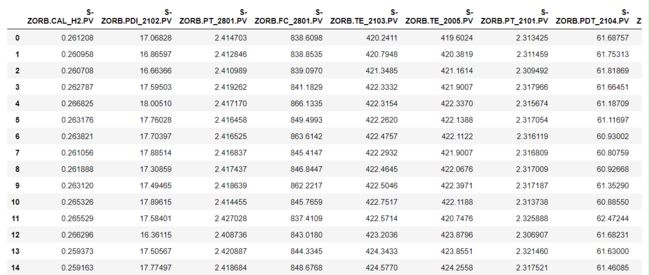
data=pd.read_excel('附件三：285号和313号样本原始数据.xlsx',sheet_name='操作变量285')
data

 

查看第一列的时间： 

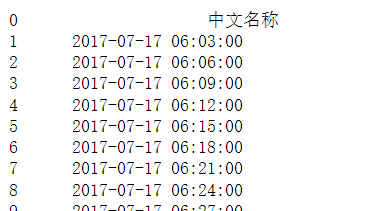
times=data.iloc[:,0]
times

这里发现时间步的间隔都是3min,查看是否存在时间步不为3的行。

from datetime import datetime, date
Seconds=[]
for i in range(1,40):
    time_i=data.iloc[i-1,0]
    time_i_1=data.iloc[i,0]
    time_i_struct = datetime.strptime(time_i.strip(), "%Y-%m-%d %H:%M:%S")
    time_i_1_struct = datetime.strptime(time_i_1.strip(), "%Y-%m-%d %H:%M:%S")
    seconds = (time_2_struct - time_1_struct).seconds
    Seconds.append(seconds/60)
Seconds

得到结果全为3，所以不用处理了。

去除空值：经过查找，不存在空值。 

 因为数据，必须满足附件四中操作变量的范围：

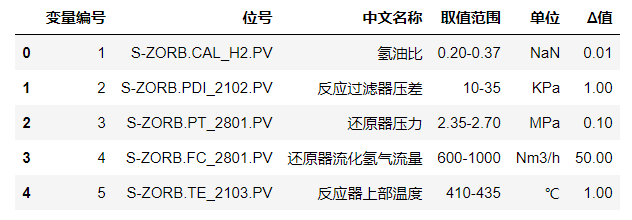
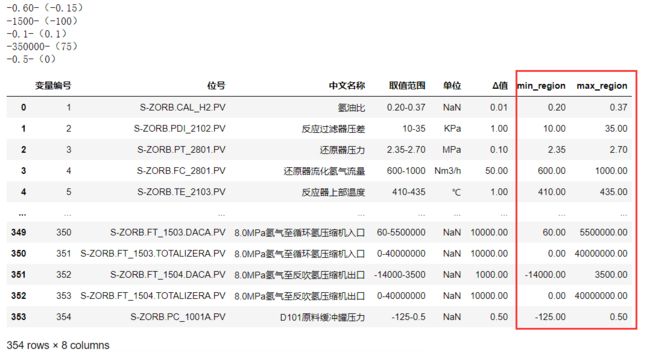
data_range=pd.read_excel('附件四：354个操作变量信息.xlsx')
data_range.head()

# 得到最大最小范围的函数

import re
# 通过符号‘-’进行分割。
def get_min_range_value(data):
    try:
        # 如果字符串的第一个字符为‘-’,说明是负数。
        if data[0]=='-':
            return -float(data.split('-')[1])
        else:
            return float(data.split('-')[0])
    except:
        print(data.split('-'))

def get_max_range_value(data):
    if ('(' in data) or (')' in data):
        try:
            temp=re.search('\((.*?)\)',data).group(1)
        except:
            temp=re.search("（(.*?)）",data).group(1)
        return float(temp)
    try:
        return float(data.split('-')[-1])
    except:
        print(data)

 添加两列，保存最大最小值：

data_range['min_region']=data_range.apply(lambda x:get_min_range_value(x['取值范围']),axis=1)
data_range['max_region']=data_range.apply(lambda x:get_max_range_value(x['取值范围']),axis=1)
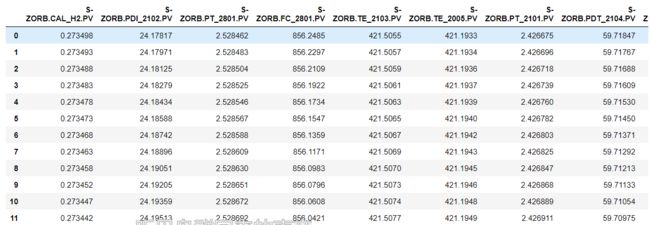
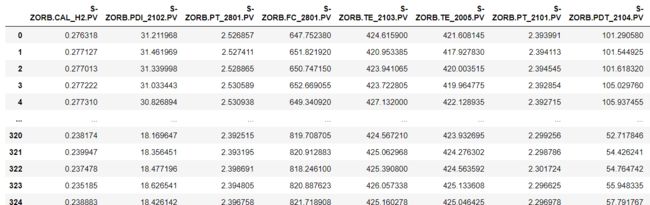
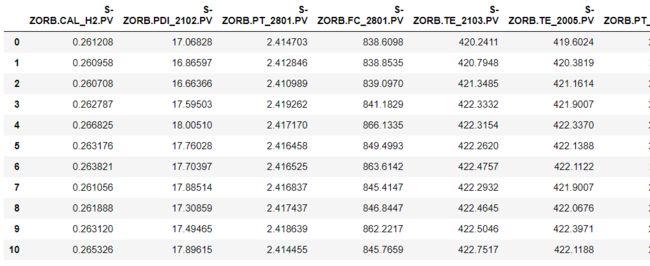
data_range

data=pd.read_excel('附件三：285号和313号样本原始数据.xlsx',sheet_name='操作变量285')
data

data=data.iloc[:,1:]
data

 检查285号样本数据不在范围内的数据点：

def check_data(data,min_values,max_values):
    if (data > max_values) or (data < min_values):
        return np.nan
    else:
        return data

查看第一列是什么 ： 

names=data_range.iloc[i,1]
names

'S-ZORB.CAL_H2.PV'

for i in range(data_range.shape[0]):
    names=data_range.iloc[i,1]
    data_min=data_range.iloc[i,6]
    data_max=data_range.iloc[i,7]
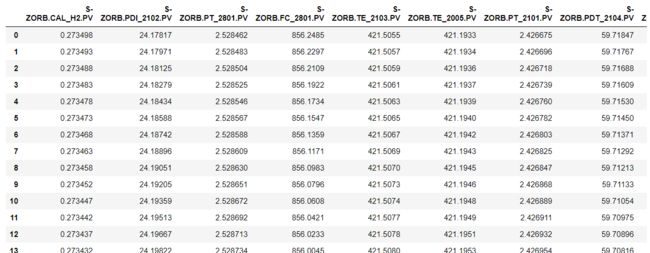
    data[names]=data[names].apply(lambda x:check_data(x,data_min,data_max))
    
data

现在已经把不在范围内的点替换成空值了。

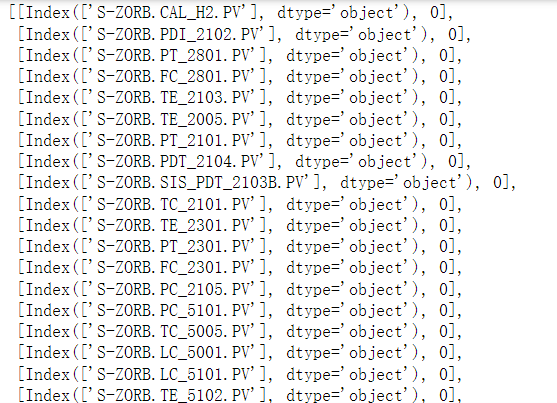
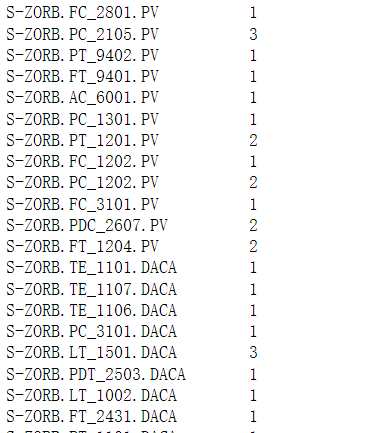
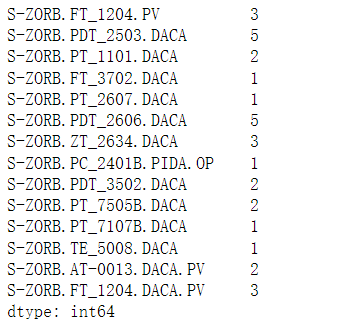
data.isnull().sum()

 

因为数据很长，我们无法准确看到究竟那一列数据空值点，我们做一步查找： 

data.isnull().sum()[data.isnull().sum()!=0]

发现这三列的数据有问题。

4.2 附件313数据的处理：

接下来分析313的数据。

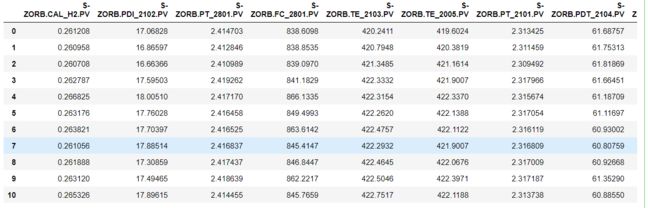
data_1=pd.read_excel('附件三：285号和313号样本原始数据.xlsx',sheet_name='操作变量313')
data_1=data_1.iloc[:,1:]
data_1

 同理检查不在范围内的数据：

def check_data(data_1,min_values,max_values):
    if (data_1 > max_values) or (data_1 < min_values):
        return np.nan
    else:
        return data_1
    
for j in range(data_range.shape[0]):
    names=data_range.iloc[j,1]
    data_min=data_range.iloc[j,6]
    data_max=data_range.iloc[j,7]
    data_1[names]=data_1[names].apply(lambda x:check_data(x,data_min,data_max))
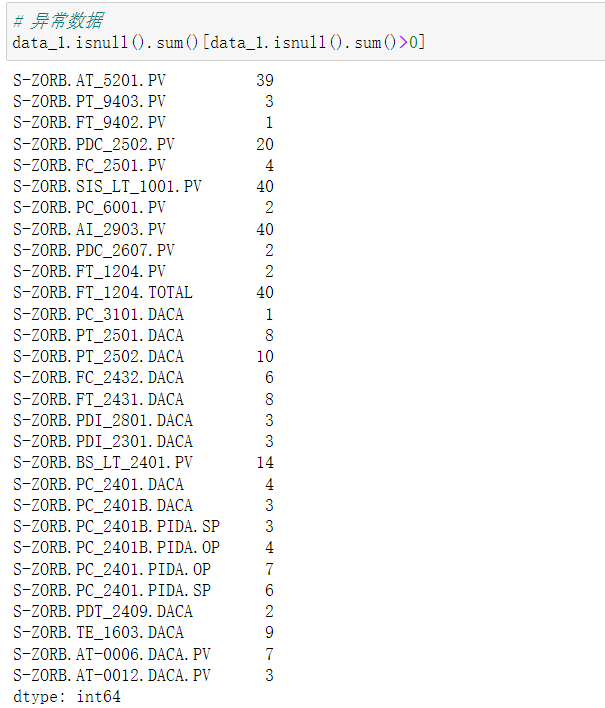
data_1

data_1.isnull().sum()[data_1.isnull().sum()>0]

 4.3附件一的处理：

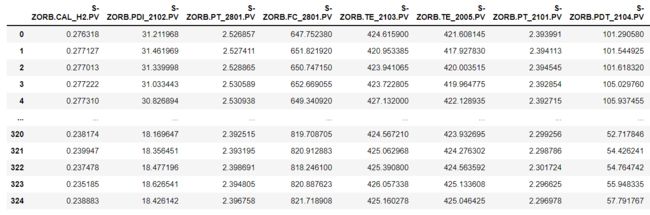
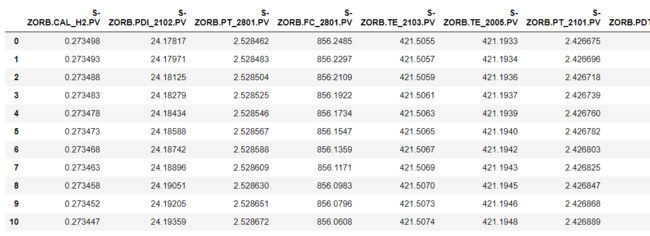
data_325_all=pd.read_excel('附件一：325个样本数据.xlsx')
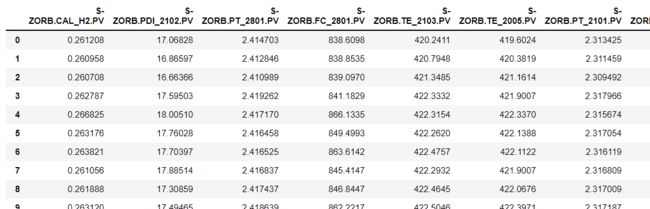
data_325_all_cao_zuo=data_325_all.iloc[:,0:]
data_325_all_cao_zuo

先对数据进行了简单的处理一下。中间的是不变的。 

def check_data(data_325_all_cao_zuo,min_values,max_values):
    if (data_325_all_cao_zuo > max_values) or (data_325_all_cao_zuo < min_values):
        return np.nan
    else:
        return data_325_all_cao_zuo
    
for j in range(data_range.shape[0]):
    names=data_range.iloc[j,1]
    data_min=data_range.iloc[j,6]
    data_max=data_range.iloc[j,7]
    data_325_all_cao_zuo[names]=data_325_all_cao_zuo[names].apply(lambda x:check_data(x,data_min,data_max))
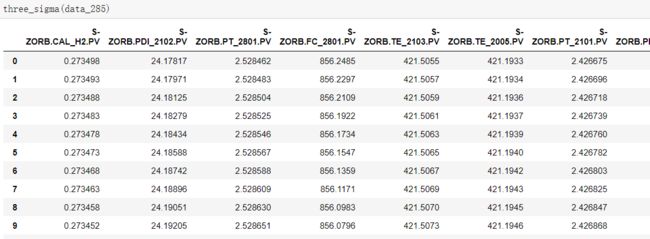
data_325_all_cao_zuo

data_325_all_cao_zuo.isnull().sum()[data_325_all_cao_zuo.isnull().sum()>0]

 

 4.4 拉以达准则

def three_sigma(df_col):
    """
    df_col:DataFrame数据的某一列
    """
    rule = (df_col.mean() - 3 * df_col.std() > df_col) | (df_col.mean() + 3 * df_col.std() < df_col)
    index = np.arange(df_col.shape[0])[rule]
    out_range_index=[pd.DataFrame(df_col.iloc[index]).columns,pd.DataFrame(df_col.iloc[index]).shape[0]]
    return out_range_index

# 285
out_range_285_idx=[]
for i in range(data.shape[1]):
    df_col=data.iloc[:,i]
    out_range_285=three_sigma(df_col)
    out_range_285_idx.append(out_range_285)
out_range_285_idx

# 计算符合数据的个数
counts=0
for m in range(len(out_range_285_idx)):
    if out_range_285_idx[m][1]==0:
        counts+=1
    else:
        counts+=0
counts

354

out_range_313_idx=[]
for i in range(data_1.shape[1]):
    df_col_1=data_1.iloc[:,i]
    out_range_313=three_sigma(df_col_1)
    out_range_313_idx.append(out_range_313)
out_range_313_idx

counts=0
for n in range(len(out_range_313_idx)):
    if out_range_313_idx[n][1]==0:
        counts+=1
    else:
        counts+=0
counts

313

找出异常数据。

# 找出异常数据

index_313=[]
for k in range(354):
    if out_range_313_idx[k][1]!=0:
        index_313.append((out_range_313_idx[k][0],out_range_313_idx[k][1]))
index_313

处理完的数据：

链接: https://pan.baidu.com/s/11OL6B3d3FV8oJ2aQlBK3Kg 提取码: 8u4u

 4.5 缺失值的处理

首先计算各位点数据的缺失值比率。将计算值与缺失值比率的阈值（20%）相比，按照其是否超过阈值将缺失数据分为两类：

（1）缺失值比率低的数据；

（2）数据缺失值比率高的数据。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data_285=pd.read_excel('附件三：285号和313号样本原始数据.xlsx',sheet_name='操作变量285')
data_285=data_285.iloc[:,1:]
data_285

data_313=pd.read_excel('附件三：285号和313号样本原始数据.xlsx',sheet_name='操作变量313')
data_313=data_313.iloc[:,1:]
data_313

 检查不符合3σ原则的数据，并标记为空值

def three_sigma(data_input):
    for i in range(data_input.shape[0]):
        for j in range(data_input.shape[1]):
            mean=data_input.iloc[:,j].mean()
            std=data_input.iloc[:,j].std()
            if abs(data_input.iloc[i,j]-mean)>3*std:
                data_input.iloc[i,j]=np.nan
            else:
                continue
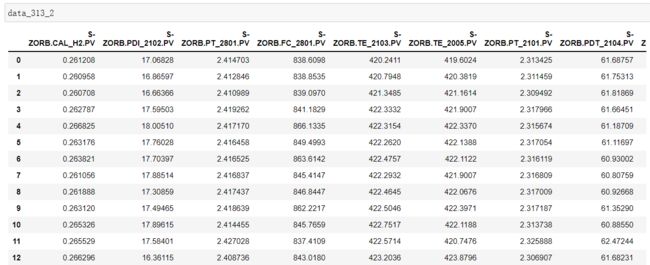
    return data_input

我们看一下313的数据集： 

data_313_2=three_sigma(data_313)
data_313_2

data_313_2.isnull().sum()[data_313_2.isnull().sum()>0]

 

第一列为索引位置，我们检查一下空值的位置： 

isnull=[]
for i in data_313_2.columns:
    for j in data_313_2.index:
        if data_313_2.isnull().loc[j,i]:
            isnull.append((j,i))
isnull,len(isnull)
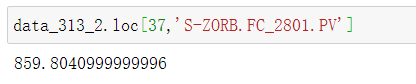
# 检查一下空值的位置 第一列为索引位置

 尝试查看一个：

data_313_2.loc[37,'S-ZORB.FC_2801.PV']
# 尝试一个

nan

from scipy.interpolate import lagrange
#传入存在缺失值的列，缺失值所在0轴坐标index，按前后k个数来计算拉格朗日插值，返回index的拉格朗日插值
def lag_fill(df,i,k):
    r=0 if (i-k)<0 else (i-k) # python的三目运算符较为特殊
    l=len(df.index) if (i+1+k)>len(df.index) else (i+1+k)
    y=df.loc[list(range(r,i))+list(range(i+1,l))] #取index前后k个数据作为y代入拉格朗日函数进行拟合
    for j in y.index:
        if y.isnull().loc[j]:
            y.drop(index=j,inplace=True)
    x=y.index
    lag=lagrange(x.values,y.values)
    return lag(i)

for i in isnull:
   fnum=lag_fill(data_313_2.loc[:,i[1]],i[0],1)
   data_313_2.loc[i[0],i[1]]=fnum

我们检验一下新数据据是否合适： 

# 用3sigma 函数在检验一下
data_313_2_new=three_sigma(data_313_2)
data_313_2_new

data_313_2_new.isnull().sum()[data_313_2_new.isnull().sum()>0]

isnull_2=[]
for i in data_313_2_new.columns:
    for j in data_313_2_new.index:
        if data_313_2_new.isnull().loc[j,i]:
            isnull_2.append((j,i))
isnull_2,len(isnull_2)

for j in isnull_2:
   fnum_1=lag_fill(data_313_2_new.loc[:,j[1]],j[0],1)
   data_313_2_new.loc[j[0],j[1]]=fnum_1

再次检查： 

data_313_2_new_2=three_sigma(data_313_2_new)
data_313_2_new_2.isnull().sum()[data_313_2_new_2.isnull().sum()>0]

isnull_3=[]
for i in data_313_2_new_2.columns:
    for j in data_313_2_new_2.index:
        if data_313_2_new_2.isnull().loc[j,i]:
            isnull_3.append((j,i))
isnull_3,len(isnull_3)

for m in isnull_3:
   fnum_2=lag_fill(data_313_2_new_2.loc[:,m[1]],m[0],1)
   data_313_2_new_2.loc[m[0],m[1]]=fnum_2

isnull_4=[]
for i in data_313_2_new_3.columns:
    for j in data_313_2_new_3.index:
        if data_313_2_new_3.isnull().loc[j,i]:
            isnull_4.append((j,i))
isnull_4,len(isnull_4)

 

for n in isnull_4:
   fnum_3=lag_fill(data_313_2_new_3.loc[:,n[1]],n[0],1)
   data_313_2_new_3.loc[n[0],n[1]]=fnum_3
    
data_313_2_new_4=three_sigma(data_313_2_new_3)
data_313_2_new_4.isnull().sum()[data_313_2_new_4.isnull().sum()>0]

 

 至此，数据处理结束。