备战数学建模14-熵权法确定指标权重系数
目录
一、熵权法理论学习
1-熵权法简介
2-熵权法的基本思路
二、应用例题分析
1-综合成绩评价例题
2-数据归一化代码
3-计算pij代码
4-计算信息熵代码
5-计算指标权重及综合得分代码
6-程序全部代码
7-绘制的图形
三、熵权法总结
一、熵权法理论学习
1-熵权法简介
层次分析确定的权重比较主观,可以使用变异系数法和熵权法,本次主要介绍熵权法。熵权法一般就几步,分别为归一化,计算指标变异性,计算信息熵,求权重。
2-熵权法的基本思路
基本思路如下:其中:归一化是把计量单位进行统一,有固定的归一化公式。
其中数据归一化具体如下所示:
计算指标变异性具体如下所示:
计算信息熵,如下所示:
计算信息熵冗余度,具体如下:
计算出各项指标的权重,如下所示:
计算综合得分,具体如下所示:
二、应用例题分析
1-综合成绩评价例题
应用熵权法分配各项指标的权重,并根据权重计算得分,进而进行成绩排名。
2-数据归一化代码
%指标归一化处理
z = zeros(7, 1) ;
for i = 1 : m
if ind(i) == 1 %正向指标归一化
for j = 1 : 7
z(j,1) = 0.998 * ((x(j,i) - min(x(:,i))) / (max(x(:,i)) - min(x(:,i)))) + 0.002 ;
end
X(:,i) = z ;
else %负向指标归一化
for j = 1 : 7
z(j,1) = 0.998 * (max(x(:,i)) - (x(j,i)) / (max(x(:,i)) - min(x(:,i)))) + 0.002 ;
end
X(:,i) = z ;
end
end
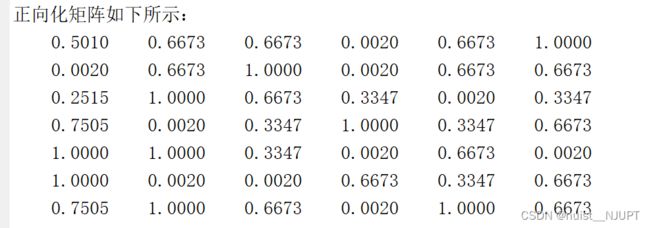
disp('正向化矩阵如下所示:') ;
disp(X) ;
得到归一化后的矩阵如下所示:
3-计算pij代码
%计算第j个指标下第i个样本占该指标的比重pij
for i = 1 : n
for j = 1 : m
p(i,j) = X(i,j) / sum(X(:,j)) ;
end
end
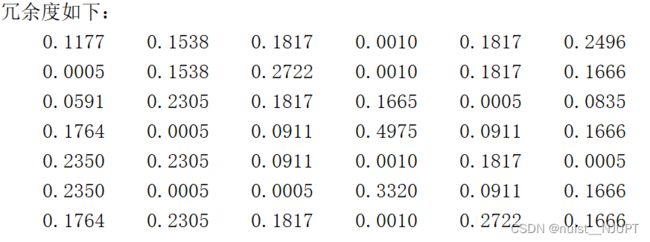
disp('冗余度如下:') ;
disp(p) ;4-计算信息熵代码
%计算第j个指标的信息熵
k = 1 / log(n) ;
for j = 1 : m
e(j) = -k * sum(p(:,j) .* log(p(:,j))) ;
end
disp('每个指标的信息熵如下:')
disp(e) ;5-计算指标权重及综合得分代码
d = ones(1, m) - e ; % 计算信息熵冗余度
w = d ./ sum(d) ; %计算权重
disp('每个指标的权重如下:') ;
disp(w) ;
s = X * w' ; %计算综合得分
disp('每个同学的综合得分如下:') ;
disp(s) ;6-程序全部代码
clear; clc
x = [80 90 90 70 90 90
60 90 100 70 90 80
70 100 90 80 70 70
90 70 80 100 80 80
100 100 80 70 90 60
100 70 70 90 80 80
90 100 90 70 100 80
] ;
ind = ones(size(x,2), 1) ; %正向化指标初始化为1,负向化指标初始化为2
[n, m] = size(x) ; %n个样本,m个指标
%指标归一化处理
z = zeros(7, 1) ;
for i = 1 : m
if ind(i) == 1 %正向指标归一化
for j = 1 : 7
z(j,1) = 0.998 * ((x(j,i) - min(x(:,i))) / (max(x(:,i)) - min(x(:,i)))) + 0.002 ;
end
X(:,i) = z ;
else %负向指标归一化
for j = 1 : 7
z(j,1) = 0.998 * (max(x(:,i)) - (x(j,i)) / (max(x(:,i)) - min(x(:,i)))) + 0.002 ;
end
X(:,i) = z ;
end
end
disp('正向化矩阵如下所示:') ;
disp(X) ;
%计算第j个指标下第i个样本占该指标的比重pij
for i = 1 : n
for j = 1 : m
p(i,j) = X(i,j) / sum(X(:,j)) ;
end
end
disp('冗余度如下:') ;
disp(p) ;
%计算第j个指标的信息熵
k = 1 / log(n) ;
for j = 1 : m
e(j) = -k * sum(p(:,j) .* log(p(:,j))) ;
end
disp('每个指标的信息熵如下:')
disp(e) ;
d = ones(1, m) - e ; % 计算信息熵冗余度
w = d ./ sum(d) ; %计算权重
disp('每个指标的权重如下:') ;
disp(w) ;
s = X * w' ; %计算综合得分
disp('每个同学的综合得分如下:') ;
disp(s) ;
plot(1:7, s) ; %画图看看
7-绘制的图形
三、熵权法总结
下面总结了熵权法确定权重系数的优缺点,具体如下所示: