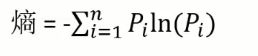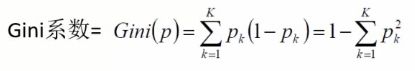机器学习系列(7)_决策树与随机森林概念
注:本篇博客参考 b站:机器学习经典算法(2)——决策树与随机森林
文章目录
- 一、熵与基尼系数
- 二、决策树构造实例
- 三、信息增益(ID3算法)
- 四、信息增益率(C4.5算法)
- 五、二分选值
- 六、决策树减枝
- 七、随机森林
一、熵与基尼系数
- 熵和基尼系数越大,说明当前分类效果越不好
- 熵和基尼系数越小,说明当前分类效果越好
二、决策树构造实例
构造树的基本想法是随着树深度的增加,节点的熵迅速地降低。熵降低的速度越快越好,这样我们有望得到一棵高度最矮的决策树。
熵降低的速度越快越好:能有三步构造决策树,就不使用五步构造决策树。要使决策树的分类层次少。
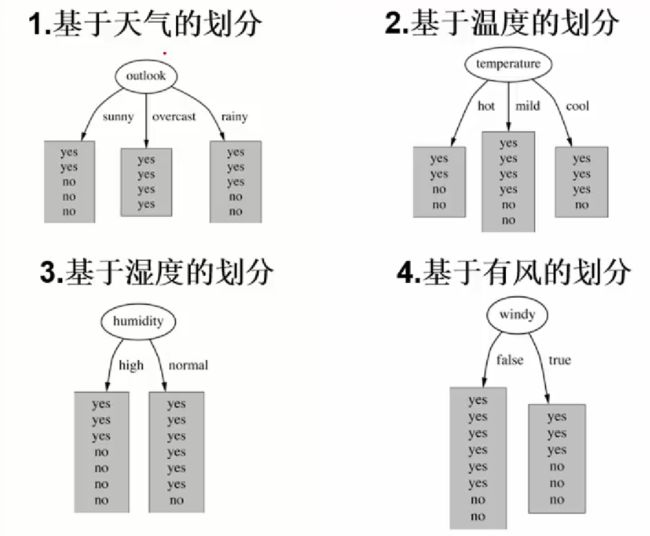
以打球为例:
此时的熵是单纯根据以往是否打球来计算的概率,没有考虑天气等其他因素:


三、信息增益(ID3算法)
ID3算法(信息增益):较为传统的算法,使用信息增益构建决策树。
信息增益就是将原始的熵减去用某个指标当根节点之后的熵。
在本例中就是如下所示的gain(outlook)

信息增益越大,那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量。
因此将四个参数的信息增益值计算出来,信息增益最大的就是根节点。
其余的节点也是一样的,类似于一个递归的操作,每次都选择同类型当中信息增益大的作为节点。
四、信息增益率(C4.5算法)
通常仅使用信息增益来绘制决策树是不靠谱的,如果某个特征存在的属性很多,但是属性对应样本的个数很少,这种情况下信息增益很大,但却无法得到我们想要的效果。
比如将ID也当成一个特征,那么每个样本的ID都是不同的,且每个样本分类当中只有自身,因此纯度很高,熵为0,信息增益最大。但这将导致每个样本都分成一类,不是我们期望的。
因此引入信息增益率。
信息增益率=信息增益 / 自身的熵值
如何衡量最终决策树的效果呢,可以使用评价函数:

这里使用H(t)表示每个叶子节点算出的基尼系数或者熵值,最终目的希望每个叶子节点的纯度很大,因此希望H(t)很小。
因此评价函数越小越好。
C4.5算法是ID3算法的扩展
能够处理连续型的属性。首先将连续型属性离散化,把连续型属性的值分成不同的区间,依据是比较各个分裂点Gian值的大小。
缺失数据的考虑:在构建决策树时,可以简单地忽略缺失数据,即在计算增益时,仅考虑具有属性值的记录。
五、二分选值
六、决策树减枝
即让决策树的层数较小,高度较矮。因为如果决策树很高的话,最终在训练集上都能达到100%的纯度,但是对于测试集,就可能造成误差,产生过拟合,因此需要让决策树的层数较小,高度较矮。
- 预剪枝:在构建决策树的过程时,提前停止。
即指定决策树的深度,比如指定为3,则分到第三层之后就停止继续分层了。
或者指定min_sample,就是当样本小于50个的时候,就停止继续分枝。
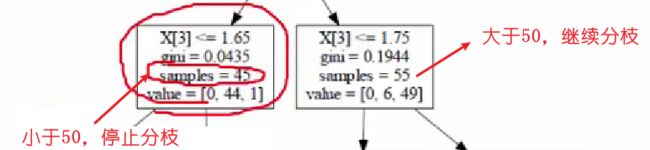
为什么要进行预减枝?为了防止过拟合的风险。
- 后剪枝:决策树构建好后,然后才开始裁剪。
 因为叶子节点个数越多,越琐碎,则越容易造成过拟合。
因为叶子节点个数越多,越琐碎,则越容易造成过拟合。
最终要使得上图的公式值最小。
上面公式中的a值可以手工指定的:
如果a较大,则叶子节点个数要少
如果a较小,则叶子节点个数可以较多
七、随机森林
森林:多颗决策树就构造了一片森林。
随机森林:构造出来一片决策树,用一片决策树都完成决策的操作,每个决策树都单独执行决策的操作,最终的结果去所有决策树的众数。
随机: 由于样本可能有异常值,因此要进行随机的选择。一共有两重的随机性:
-
数据的选择随机性
随机森去的样本是有放回的(就是可以有完全相同的样本),而且比例是随机的,都是在原始的训练集进行随机的选择。 -
特征选择的随机性
-
Bootstraping有放回采样
-
Bagging:有放回采样n个样本一共建立.分类器
决策树的参数:这些参数主要是觉得决策树怎么预减枝和后减枝的问题,防止过拟合的问题。
1、 criterion: 特征选取方法,可以是gini(基尼系数),entropy(信息增益),通常选择gini,即CART算法,如果选择后者,则是ID3和C4,.5
2、 splitter: 特征划分点选择方法,可以是best或random,前者是在特征的全部划分点中找到最优的划分点,后者是在随机选择的部分划分点找到局部最优的划分点,一般在样本量不大的时候,选择best,样本量过大,可以用random
3、 max_depth: 树的最大深度,默认可以不输入,那么不会限制子树的深度,一般在样本少特征也少的情况下,可以不做限制,但是样本过多或者特征过多的情况下,可以设定一个上限,一般取10~100
4、 min_samples_split:节点再划分所需最少样本数,如果节点上的样本树已经低于这个值,则不会再寻找最优的划分点进行划分,且以结点作为叶子节点,默认是2,如果样本过多的情况下,可以设定一个阈值,具体可根据业务需求和数据量来定
5、 min_samples_leaf: 叶子节点所需最少样本数,如果达不到这个阈值,则同一父节点的所有叶子节点均被剪枝,这是一个防止过拟合的参数,可以输入一个具体的值,或小于1的数(会根据样本量计算百分比)
6、 min_weight_fraction_leaf: 叶子节点所有样本权重和,如果低于阈值,则会和兄弟节点一起被剪枝,默认是0,就是不考虑权重问题。这个一般在样本类别偏差较大或有较多缺失值的情况下会考虑
7、 max_features: 划分考虑最大特征数,不输入则默认全部特征,可以选 log2N,sqrt(N),auto或者是小于1的浮点数(百分比)或整数(具体数量的特征)。如果特征特别多时如大于50,可以考虑选择auto来控制决策树的生成时间
8、 max_leaf_nodes:最大叶子节点数,防止过拟合,默认不限制,如果设定了阈值,那么会在阈值范围内得到最优的决策树,样本量过多时可以设定
9、min_impurity_decrease/min_impurity_split: 划分最需最小不纯度,前者是特征选择时低于就不考虑这个特征,后者是如果选取的最优特征划分后达不到这个阈值,则不再划分,节点变成叶子节点
10、class_weight: 类别权重,在样本有较大缺失值或类别偏差较大时可选,防止决策树向类别过大的样本倾斜。可设定或者balanced,后者会自动根据样本的数量分布计算权重,样本数少则权重高,与min_weight_fraction_leaf对应
11、presort: 是否排序,基本不用管