算法 | 二分法与折半插入排序【这是开端吗？】

概念引入

二分查找法

对于二分搜索，大家应该在学习C语言的时候就接触过了，但那时候只是了解了它的代码，并没有去真正实现其原理，对于左右区间的开闭问题也是了然无知，今天，就让我们一起去真正了解一下二分查找法

• 去一个区间里查找一个数，我们都会使用for循环去遍历，如果是10个数还是，但是要是100个数、10000个数呢，也是一个个去遍历查找吗，那只会显得非常的繁琐
• 这个时候我们就要去想办法把这个查找的过程进行一个简化，这里我们就应该想到二分查找这种算法，通过将需要查找的数字和两端的一个中间值进行一个比较，每次的比较都会舍弃掉一般的数据，这对于查找来说是非常的高效，很快便可以定位到我们所需要定位的元素，因此它的时间复杂度为O(log₂n)
• 当然，如果你知道哈希表的话，那无非是一种更加高效的做法，其时间复杂度可以低至O(1)，如果不懂可以看看一文带你快速入门哈希表

插入排序

接下来我们来介绍一下插入排序，本文我们所要将的折半插入排序就是插入排序的一种

• 所谓插入排序，就是将一个待排元素按其关键字大小插入到前面已经排好序的子表中的适当位置，知道全部元素插入完成为止
• 插入排序分为直接插入排序、折半插入排序以及希尔排序，其实希尔排序是这本插入排序的延伸，有兴趣的小伙伴可以去了解一下，本文重点讲解折半插入排序
• 对于折半插入排序，在我看来，它就是以二分法作为底层架构的，因此将他们两个放在一起做讲解，它对于直接插入排序来说，高效了许多。也是去利用二分法的思维，不断地缩小待查元素所在区间

---

了解了它们的基本概念，接下来就让我们进入具体的案例记性讲解

二分查找

我们通过一道具体的力扣题来分析

LeetCode.704 二分查找

原题传送门

题目描述
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

思路分析

• 对于本题，没有其他花头，就是一道二分查找的题目，首先给出题目的思路
• 代码中的参数列表给出了两个参数，一个是待查数组，一个是待搜元素

int search(vector<int>& nums, int target)

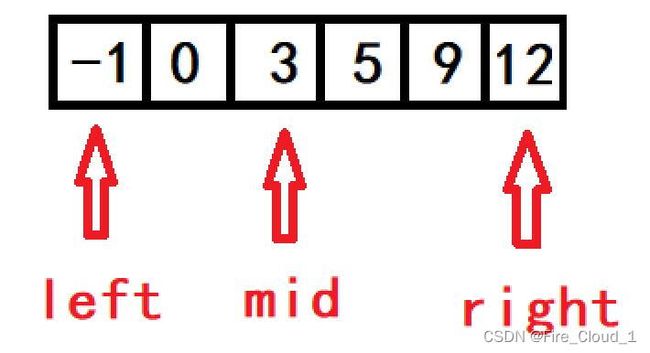
• 其实这就相当于一道双指针的题目，首先，你需要一个左指针left，指向数组的首元素，然后，你需要一个右指针right，指向数组的最后一个元素，然后就是通过循环去判断两个左右指针是否重合，这要写在一个while循环里，
• 这里就是很多小伙伴的易错点，这个left倒是<呢还是<=呢，这就要涉及到我们下面所讲的左闭右闭还是左闭右开，在循环内部我们需要取到两个左右指针的中间值，作为mid，上面有说到，通过这个数组中这个mid下标位置所在值与待查找元素进行一个比较，然后去判断这个待查元素是在mid下标的左区间还是右区间，继而去改变左边界和右边界的值
• 当然还有一个易错点就是更新左边界和右边界的位置，这个right 到底是mid - 1呢，还是mid呢，这也是要涉及到左闭右闭还是左闭右开，接下来让我们正式进入题目

左闭右闭

首先就是左闭右闭，这是大家接触最多的一种

int search(vector<int>& nums, int target) {
    int low=0;
    int high=nums.size()-1;
    while(low<=high)
    {
        int mid=low+((high-low)/2);
        if(target>nums[mid])
        {
            low=mid+1;
        }
        else if(target<nums[mid])
        {
            high=mid-1;
        }
        else return mid;
    }
    return -1;
}

• 首先我们根据指针初始图来看一下

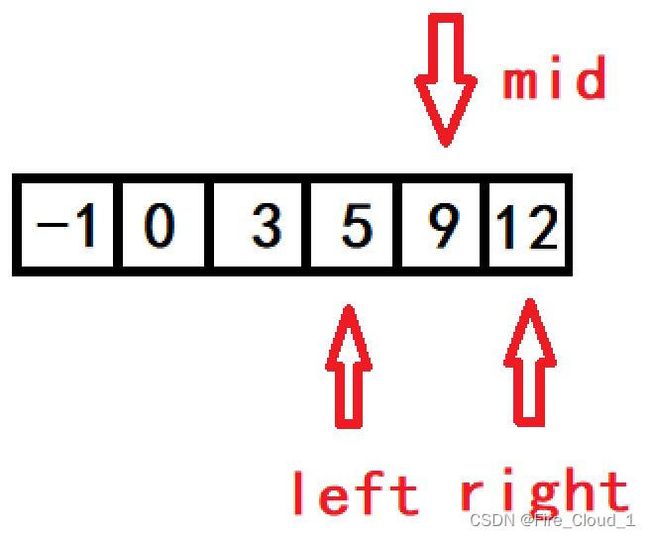
• 根据示例1，我们要查找的target是9，经过一次判断后，发现9是在nums[mid]的右边区域，说明此时我们需要更新此时的左边界，此时left应该等于mid + 1，也就是指向下标3的位置，right不变，接着取进入下一次while循环，重新去取mid的值，也就是(3 + 5)/2 = 4，故此时的mid应该指向的是下标为4的位置

• 这是就发现，此时mid所指位置上的数字不就是我们所要查找的数字吗
• 那此时就会进入else return mid;这一语句，直接将当前mid所在位置的下标返回

可以看出，使用二分法去查找一个元素，效率实在是非常得高，如果你直接通过for循环去遍历书序下标的话，那么此时就需要5步才可以到达下标为4的这个位置，真的可以说的【折半】了

左闭右开

好，讲完了左闭右闭，接下去我们来讲一下左闭右开这种情况，这就是经常让大家混淆的边界问题了

int search(vector<int>& nums, int target) {
    int left=0;
    int right=nums.size();      //不包含右区间
    while(left<right)       //left不可等于right，否则将会矛盾
    {
        int mid=(left+right)/2;
        if(target>nums[mid])
        {
            left=mid+1;     //[mid+1,right)
        }
        else if(target<nums[mid])
        {
            right=mid;  
        }
        else return mid;
    }
    return -1;
}

• 我们来看一下变化的部分
• 第一个地方就是int right=nums.size() 这一块，因为右边是开的，所以不能包含进去
• 然后最重要的地方就是左右边界的更新这一块，首先当目标数位于mid所在下标数的右侧时，就需要更新左边界，但是左边界和左闭右开时 一样，所以还是mid + 1
• 但是当目标数位于mid所在下标数的左侧时，就需要更新右边界了，因为本身就不包含右边界，所以下一次就可以包含这个边界了，也及时本次判断的不包含mid，但是下次就可以从mid开始判断，所以不需要mid - 1，只要让right = mid就行
• 最后一个地方也就是开头的while循环内，上面忘了说了，因为是[left,right)所以，left 是不可以 == right，不然的话就会出现矛盾了。如果它们相等的话这个区间就不是一个合法的区间了×

---

好了，以上就是我们所要说的有关二分查找的所有内容，接下去我们来讲一讲折半插入排序，细心观察，你就会发现它和二分查找很类似

折半插入排序【⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐】

代码展示【五指针的跳动】

• 首先大家先看一下代码

void BinInsertSort(int a[], int n)
{
	int i, j, tmp;
	for (int i = 1; i < n; ++i)
	{
		tmp = a[i];
		int low = 0;
		int high = i - 1;
		while (low <= high)
		{
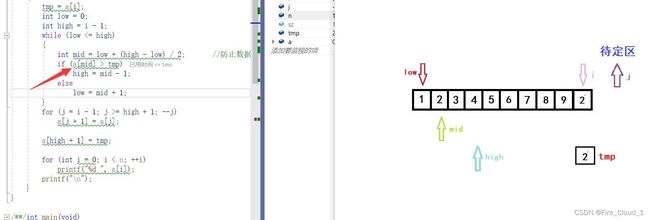
			int mid = low + (high - low) / 2;		//防止数据溢出
			if (a[mid] > tmp)
				high = mid - 1;
			else
				low = mid + 1;
		}
		for (j = i - 1; j >= high + 1; --j)
			a[j + 1] = a[j];

		a[high + 1] = tmp;

		for (int i = 0; i < n; ++i)
			printf("%d ", a[i]);
		printf("\n");
	}
}

手撕 + 分步图解【有详细的DeBug过程】

• 首先从一下这张图我们可以看出，插入排序是属于比较稳定的一种内排序，对于时间复杂度来说最好可以到达O(n)，最坏是O(n²)
• 说它是稳定的，是什么意思呢，也就是如果有相同的两个数字，那么在排序完后这相同的两个数字的相对顺序是不会发生改变的

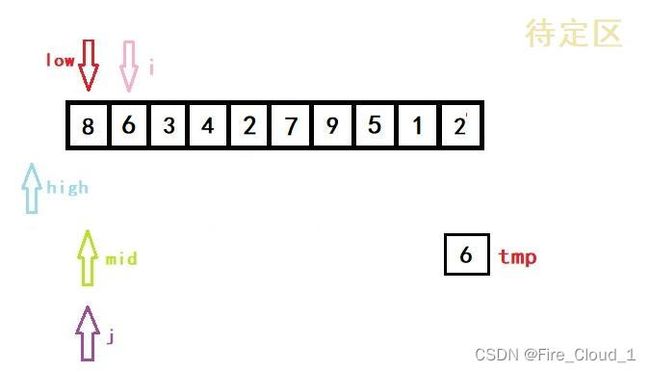
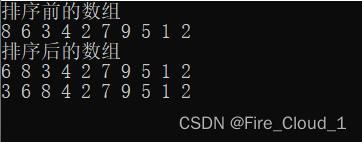
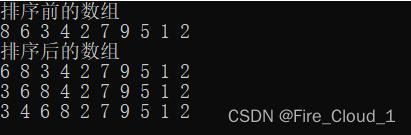
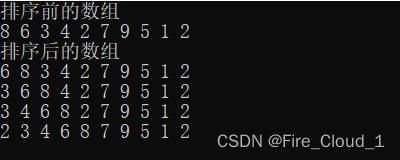
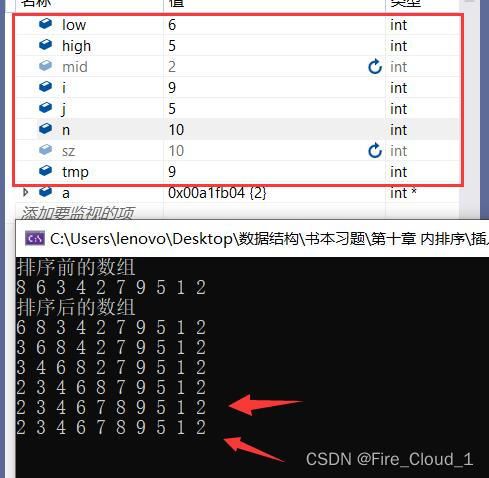
• 我们以这组数据为例8 6 3 4 2 7 9 5 1 2
• 可以看到，我专门在这组数据里设置了两个相同的数字，为的就是看出它是否真的稳定

准备上车，开始了

Part1
8 6 3 4 2 7 9 5 1 2

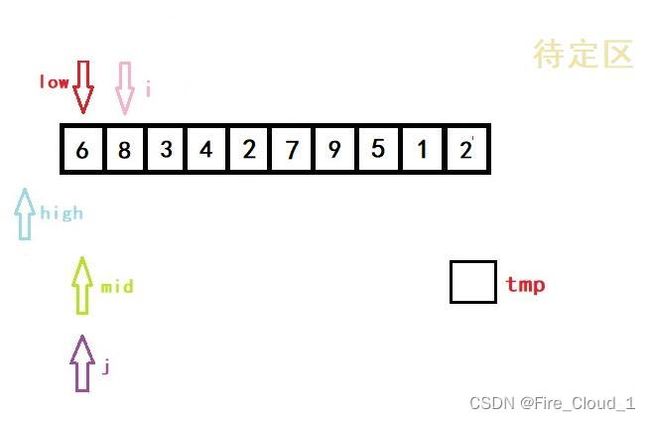
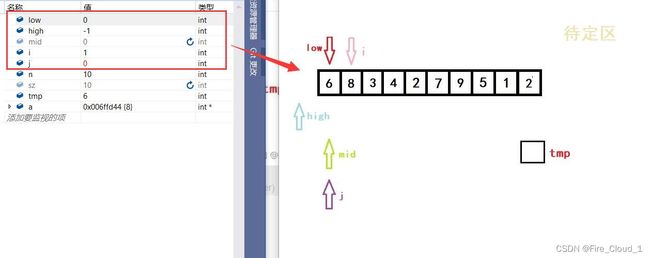
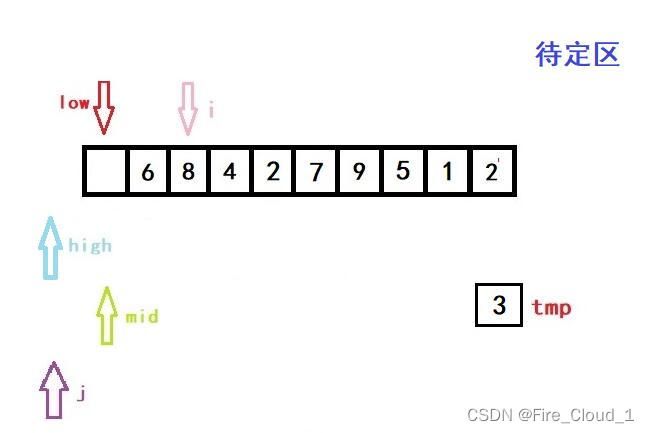
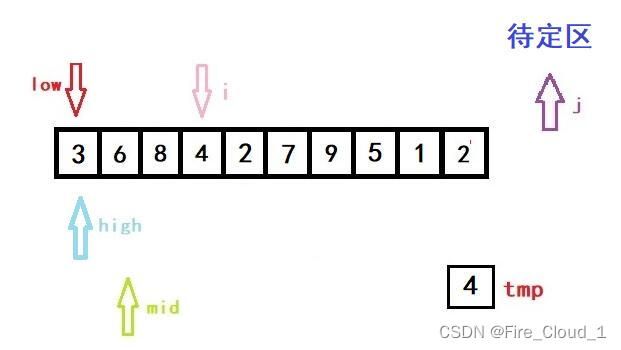
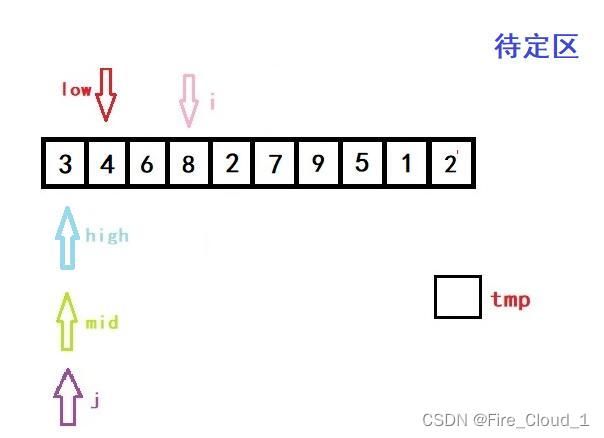
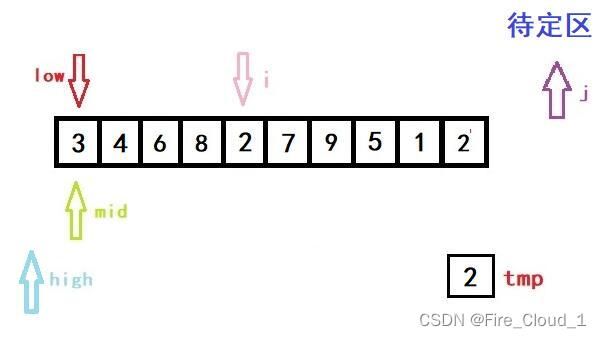
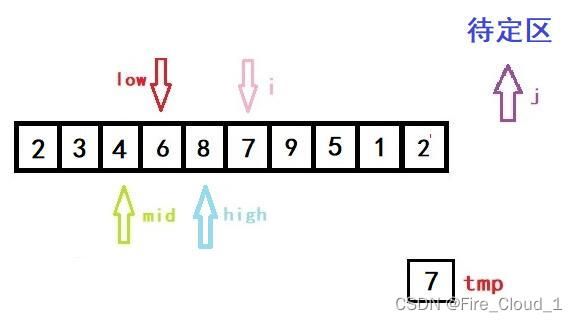
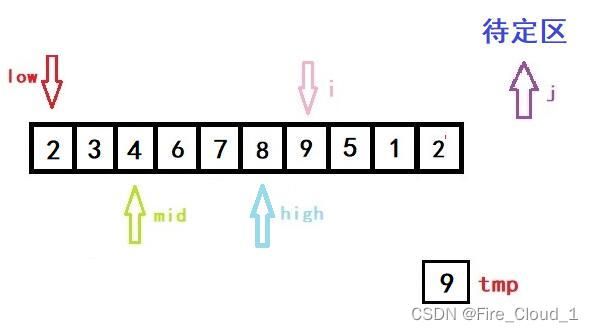
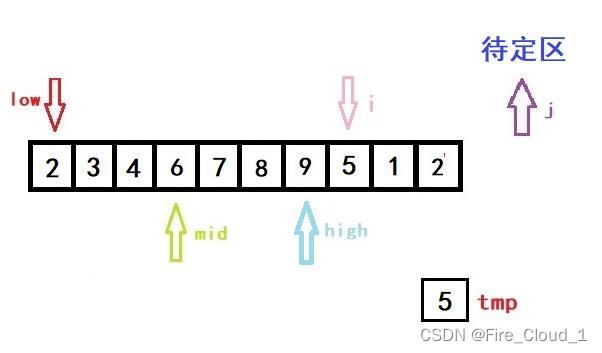
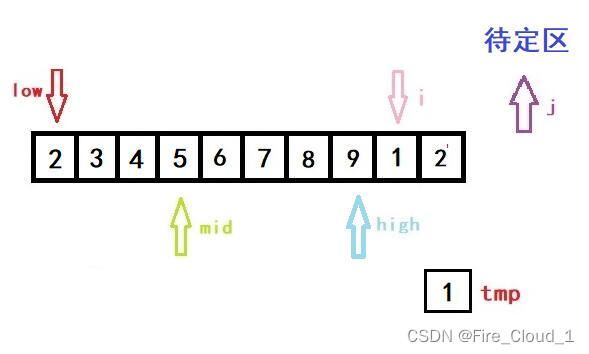
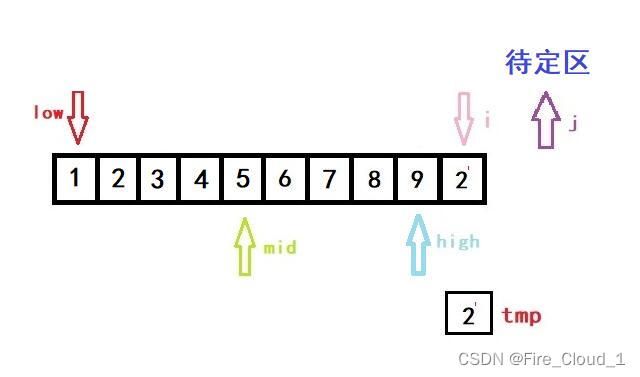
• 首先进行初始化，将开始遍历的第一个数放入tmp中暂时存放起来。说一下为什么从1开始，而不是从0开始，因为第一个数字那就是只有一个数字，是不需要去排序的，所以为了效率，从第二个开始就行，也就是下标1的位置
• 然后第一次进入循环，一样是初始化left，righ和mid的位置，以及i的位置
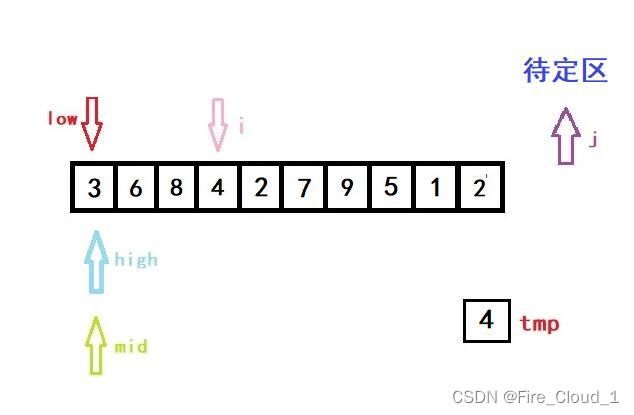
• 可以看到，此时low、high与mid都是指向同一位置的

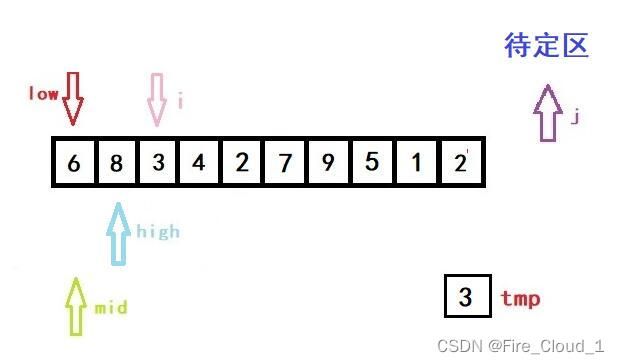
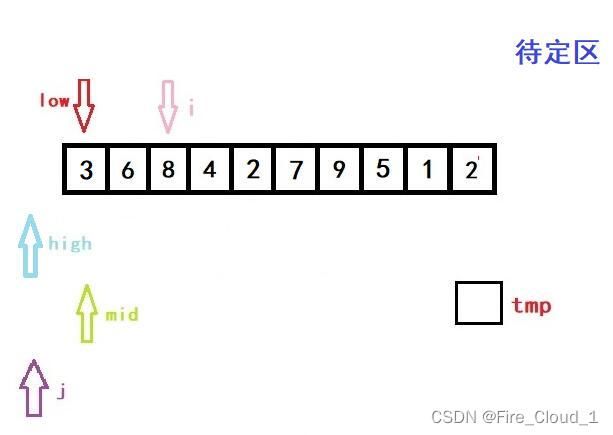
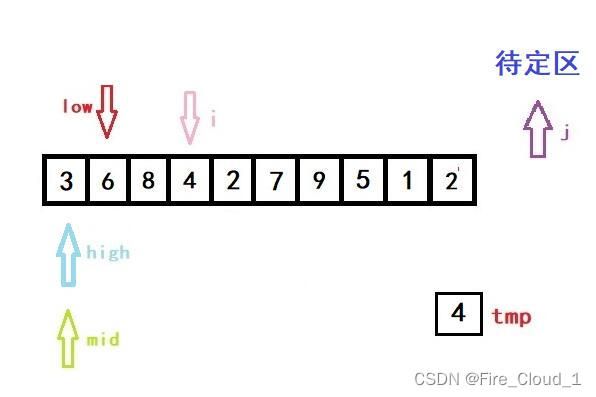
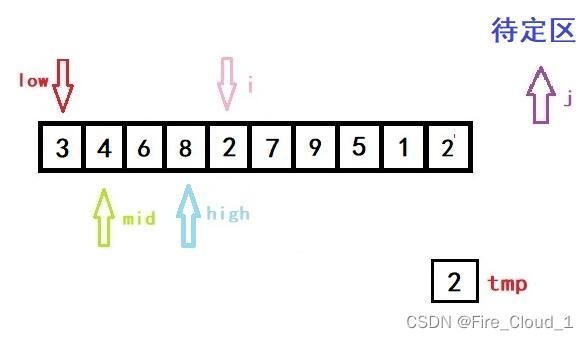
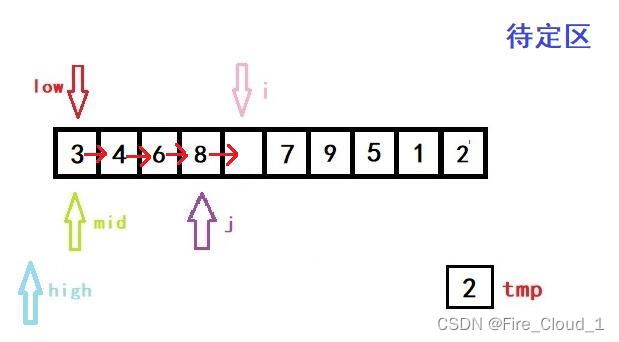
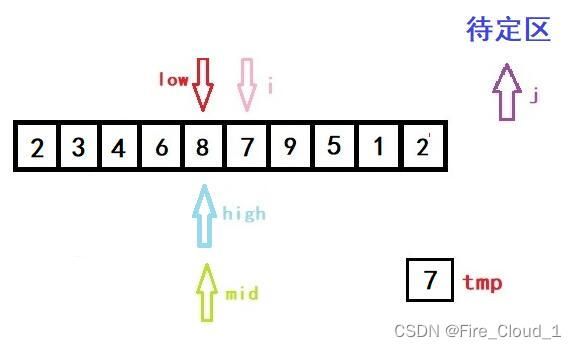
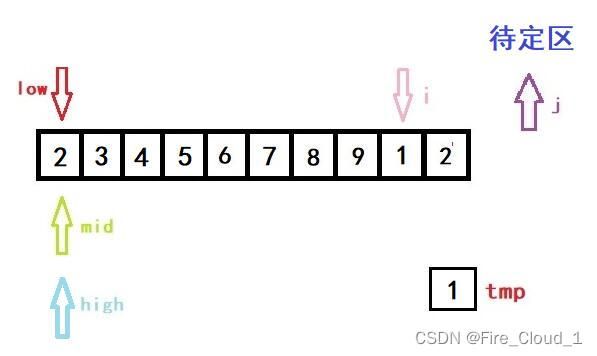
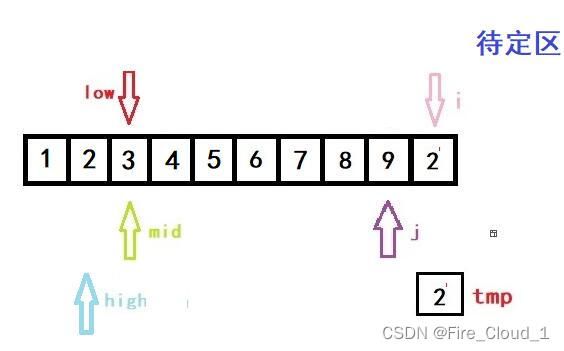
• 接着进入if分支判断，因为tmp是要小于当前mid所在位置数字的，所以我们要更新high的值。但是更新完后high就小于low了，此时就要跳出while循环，进入我们的数组移位操作循环的部分
• 这个时候j就要上场了，它可起到一个至关重要的作用

for (j = i - 1; j >= high + 1; --j)
	a[j + 1] = a[j];

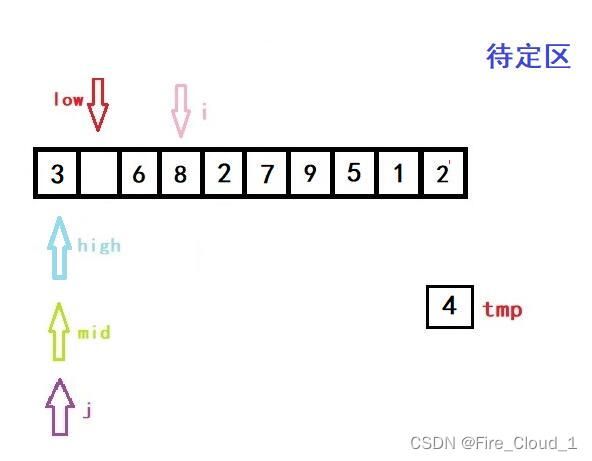
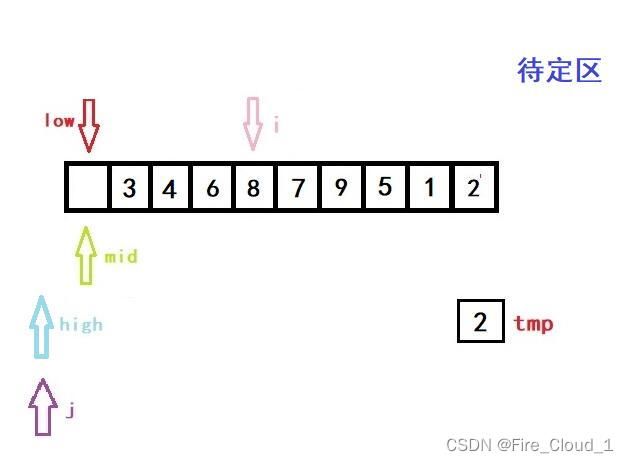
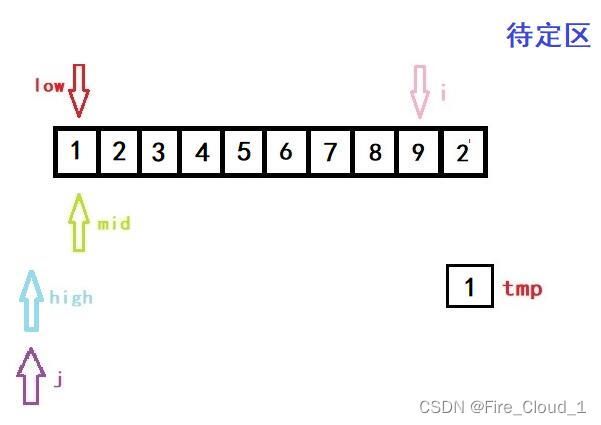
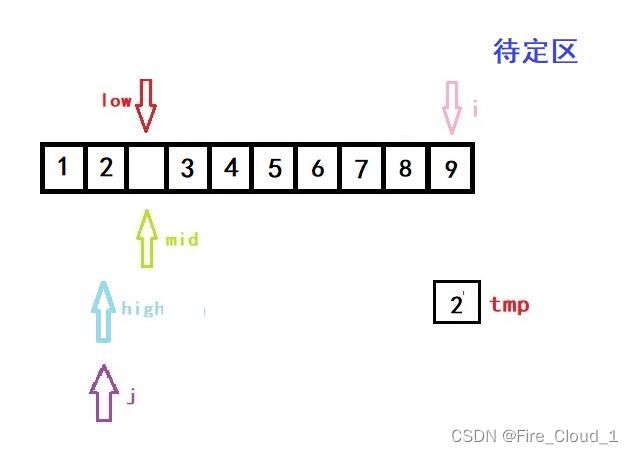
• 好，我们看到上面这段循环，j 是等于i -1,然后一直进行一个数组后移的操作，但这里只有一个元素要动，所以不明显，将a[j + 1]的位置替换成 j 的位置，这个时候呢，再执行这一步操作,就完成了第一次的排序操作

a[high + 1] = tmp;

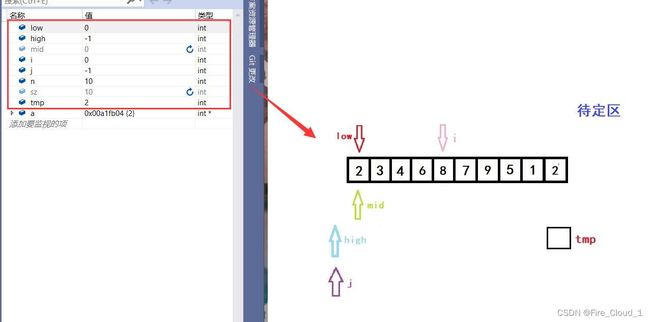
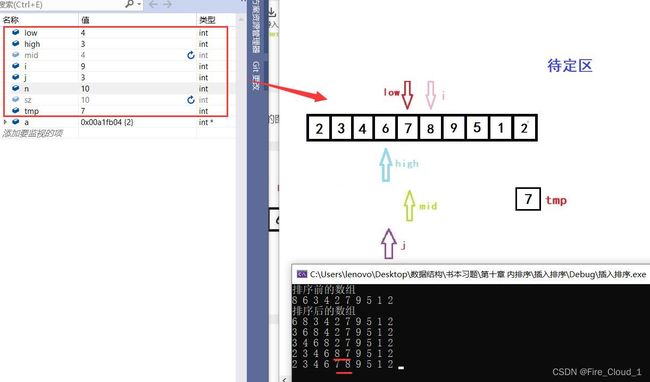
• 我们同步再来VS里看一下DeBug的数据
• 可以看出，是完全吻合的，所谓【万事开头难，后面会更难】，不要放弃哦❤️

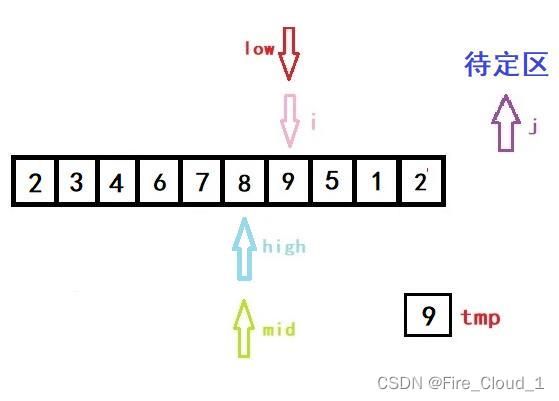
Part2
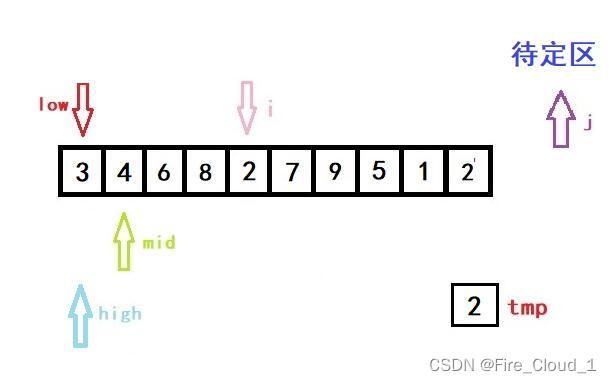
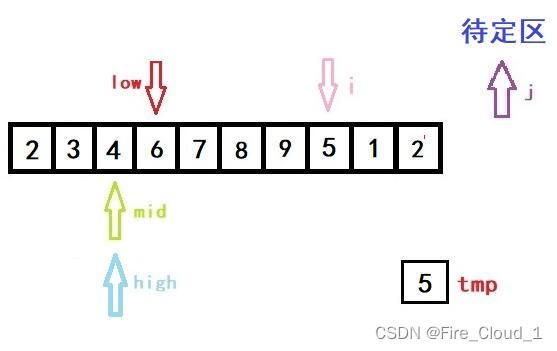
6 8 3 4 2 7 9 5 1 2

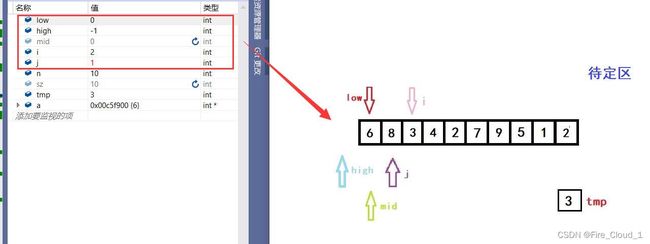
• 好，接下来进行第二次的换位移动，每次移动将会重置所有的指针，首先来看初始化指针

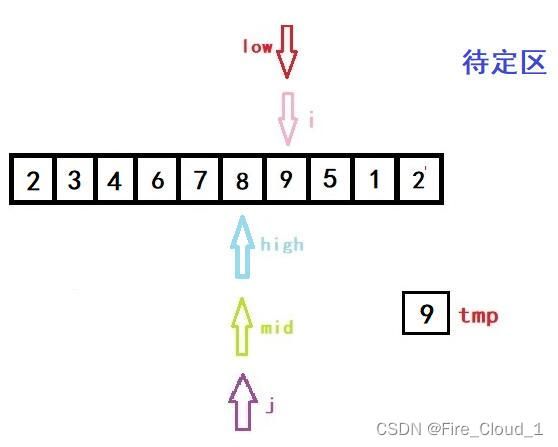
• 接下来将mid上的值与tmp进行比较，很明显3<6，所以要更新high的位置
• 再来看一下此时的DeBug调试

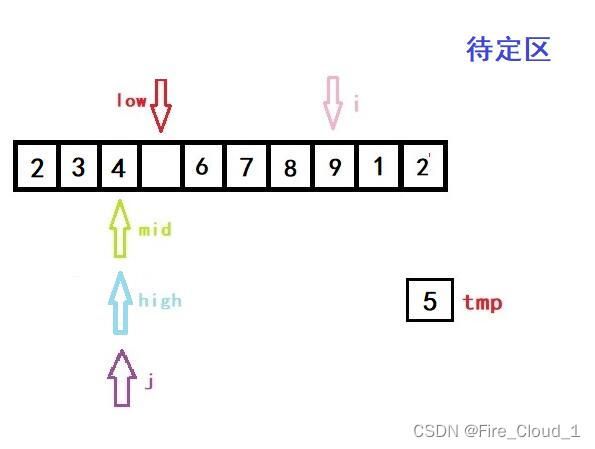
• 然后开始移动数字

• 因为不能一张张图片全放出来，所以大家要考自己想想了，这个 j 是一个前移的过程，循环的终止条件是j >= high + 1，所以当 j 等于 high的时候，此时可以看到，6 和 8 都向后移动了，这个时候high + 1的位置就空了出来，我们便执行这句话

a[high + 1] = tmp;

• 执行完后就是这样，3被放入下标为0的位置，第二步排序完成

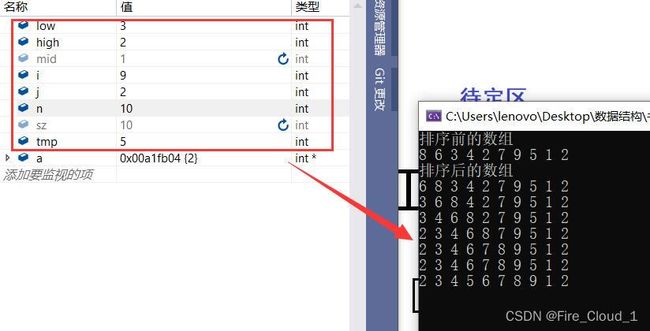
• 此时可以去看一下DeBug的调试窗口，这便是我们前两次所排好序的数组，虽然在你看来我们用了很多步骤，但是这比直接插入排序会高效地多

Part3
3 6 8 4 2 7 9 5 1 2

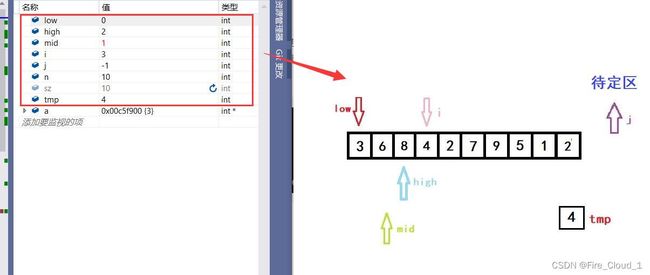
• 然后进入第三步的操作，重置所有指针，i 后移一位，进行一个初始化

• 对于tmp与a[mid]，可以看到4 < 6，所以又要更新high的位置，前面忘了说，这个high和low也是始终初始处于一个变化的过程，直到high < low为止才跳出while循环，此时low == high是还会再进入循环的

• 此时可以看到mid的值又发生了变化，要让tmp上的值继续与a[mid]进行一个比较，很明显4 > 3

• 所以此时应该去更新low的值，low = mid + 1，因为我们用得是左闭右闭区间，所以不用去考虑边界问题

• 可以看到，此时的low > high，所以这个时候就会跳出while循环，开始数字的移位操作

• 可以看到，此时 j 的位置已经是移动到了与high 一同，≠ high + 1了，所以会跳出移动数字的循环，执行这一句代码

a[high + 1] = tmp;

• 继续来看一下此时运行窗口的排序结果，与我们的完全吻合

Part4
3 4 6 8 2 7 9 5 1 2

• 接下来开始第四步，重置所有指针，i 后移一位

• 此时一样做比较2 < 4，所以我们要更新high 的位置, high = mid - 1

• 此时low == high ，继续进入循环，更新mid的值。因为2 < 3，所以继续更新high的值

• 此时的high已经是 < low 了，所以会跳出while循环进入移位的操作
• 刚好移动的位数比较多，给大家看一下原理吧

• 这个时候j == high，跳出循环，将tmp中的值放入空位即可
  
• 再来看一下DeBug图和排序后的数组

• 可以看到2被移到了最左边，这个时候要看牢了这个2和最后面那个2，到最后排序完这两个2的相对位置是不会发生改变的

Part5
2 3 4 6 8 7 9 5 1 2

• 接下来我们都可以清楚，就是将这个7移动到8的前面,7 > 4，low换位

• 下面是移动后的图示

• 从下列结果可以看出，7被移动到了8的前面

Part6
2 3 4 6 7 8 9 5 1 2

• 继续第6步，重置所有指针，此时我们要移动的是9这个数字，但是可以看出，9是不需要移动的，让我们来看看指针是如何变化的

• 从下图可以看出,low一直是在后移的一个操作，因为9这个数字实在太大了，所以不停地缩小查找的返回，这样印证了二分法的思维

• 可以看出，此时low > high，跳出while 循环，进行移位操作

• 可以看到，当第一部初始化 j 时，就已经满足了这个循环的结束条件，因此根本不会进入这个循环，直接进行这一步操作

a[high + 1] = tmp;

• 但是呢，此时的a[high + 1]与tmp又是相等的，所以这就很戏剧化，其实是做了移位操作的，只是你看不出来而已

• 可以看到，此时排序后的数组较上次是没有发生变化的，但是我们细究其原理后，就发现其实它是发生了变动的

Part7【不想看的小伙伴可以直接拉到最后了，看到这里你已经没问题了】
2 3 4 6 7 8 9 5 1 2

• 接下来继续初始化，重置所有指针，这一步要移动的是5

• 此时移动直至low > high为止

• 直到移位完成，这里就不是很详细了，节奏会快一些
• 然后将5放入对应位置即可

• 移位后便成了这样

Part8
2 3 4 5 6 7 8 9 1 2

• 细心的小伙伴应该可以发现，上面的这个数字我是一直在修改的，尽量是做一个同步
• 接下就要移动【1】了，重置所有指针，i 后移

• 可以看到这个high是一直在前移的，因为这个1太小了，需要不断地缩范围

• 直到high < low为止，就要开始一个乾坤大挪移了，因为这个1要挪到最前面

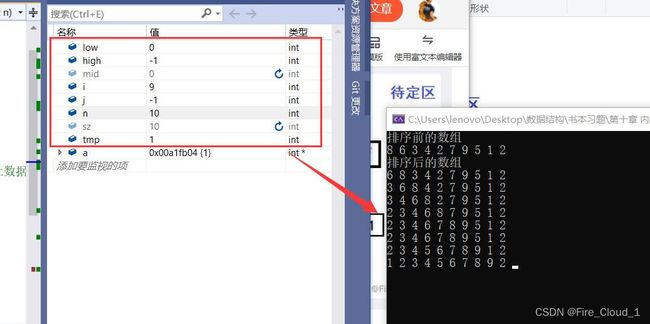
• 可以看到，1被挪到了最前面，来VS再看看，可以看到我们的数据与编译器里也是完全吻合

Part9
1 2 3 4 5 6 7 8 9 2

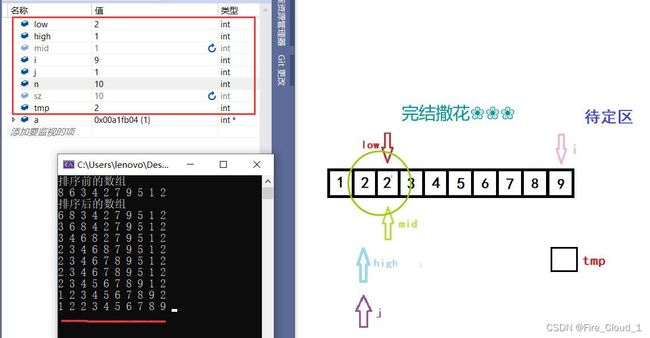
• 好，终于到最后一步了，这一步至关重要，我们要移动这个2，但是又要去证明这个2不可以跑到前面那个2的位置，才能体现出折半插排的稳定性，让我们一起来试试看

• 一定要注意tmp中这个2哦，我在右上角加了一个红色的标记

• 可以看到，此时的a[mid]与tmp的值是相等的，这个时候我们应该要进入第二个if-else分支

• 然后low与high的值便变化成这样，接下来进行数字的后移

• 可以看到，此时high + 1的位置是空出来的，执行下面这个语句将tmp中的数字放入即可

a[high + 1] = tmp;

• 以上就是折半排序后的结果，这个2没有改变其相对顺序，可以证明这个排序是稳定的

我们总共花了9个步骤去分步完成每一次的遍历循环然后插入排序，可见折半插入排序都需要这些步骤，何况直接插入排序，虽说其比较稳定，但是高效的话也不能说非常高效

总结与回顾

• 好，我们来总结一下本文所讲述的内容，本文总共讲了两个模块。第一个模块是有关二分查找的，利用一道力扣题来帮助我们先行建立这个二分的思维；第二个模块就是折半插入排序，有了二分法的基础理论后，理解起来就没有这么困难了，我们经过繁琐的一步步解析，对照VS中的DeBug，对其稳定性做了一个评估，事实可以证明它确实是稳定的一个内排序。
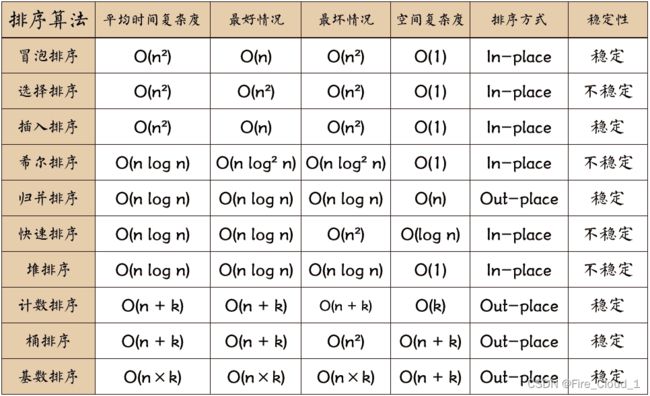
• 其实排序算法还有很多，不仅有好的内排序，像快速排序，虽然不太稳定，但是用的人较多；也有高效且受稳定的归并排序，属于外排序的一种，之后有机会再给大家做讲解

本文的内容就到这里，如有疑问请于评论区留言或者私信我，感谢您的观看