2022研究生数学建模ABCDEF思路
文章目录
-
- 选题建议和评价
- A题思路
- B题思路
- C题思路
- D题思路
- E题思路
- F题思路
- 声明一下
选题建议和评价
A题:A题偏数理知识。建议数学专业同学做,其它专业同学不要做了,研究生数学知识需要扎实。
B题:切割优化问题。相对比A简单一点。B题我要做两天,虽然难但是感兴趣,做完发出来,以前我好像做过这个题,需要可以私聊。
C题:这个调度优化问题。。不太建议这个题,也可能只是我自己不熟悉,单纯个人建议。
D题:芯片资源排布…
E题:策略问题,这个我认为最容易,有具体的指标,建议小白可以着重看这个。这个我6号半夜做完了,需要私聊。
F题:疫情管理问题,也是常见的问题,跟E题难度差不多,小白也可以选择。
最终选题建议:ABEF题还比较容易上手,可以选择,CD我反正是没看懂,单纯是个人的技术角度。基础不好的同学可以往EF走;基础好点同学建议研究下ABCD中一个。大家都做EF的话,获奖一定得保证全部做完才行。
难度评价:2022难度比2021难,主要是今年几乎没有数据题,就E题像一点,F题则比较偏向运筹方向。
至于网上那些才出题目一会就有思路出答案的人…自己斟酌吧,毕竟人家没惹我,我也不做评价。
A题思路
思路仅供参考,暂时没有时间去实践:
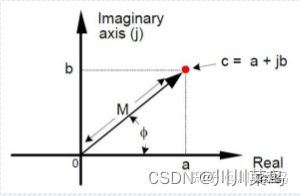
根据信号来进行定位,提示下mat文件中的复数格式的数据,是这样的,这道题主要是大家不熟悉雷达方面的定位,《雷达系统设计MATLAB仿真》这本书上有代码,可以看下,上面有很多可以用于这道题,这道题的编程不难,只要弄明白基础知识基本还是可以做。
这本书的PDF书籍下载链接:
https://wwp.lanzouv.com/ivPj80daf5kj
mat文件中的复数格式的数据,是极坐标,mat文件中,每一列表示每个周期内采集到的每一帧信号数据
load data_q1.mat
%提取实部和虚部
A=real(Z);
B=imag(Z);
%绘制极坐标
figure
plot(A(:,1),B(:,1))
xlabel('距离')
ylabel('角度')
如下:

上面是绘制每一列距离-角度的曲线,本题要解决的主要问题实则是区别多物体定位,一个物体运动情况就是上图,那么多个物体的话,数据是这样的,两种长度曲线都有,data_q1.mat是没有噪声的,但是对于后面几个mat文件,就比较麻烦
B题思路
思路仅供参考,暂时没有时间去实践:
这个排样问题很简单,有不同产品,怎么让板材利用率最大,题目是给定了需要切割产品的长宽数据,其实这个启发式算法很简单,大家也可以按我说的方式从简设计,针对种群中每个个体随机一个产品的切割顺序,板材数量不限制,其实我们看他的排样方式,以左下方为准的,那么我们就按照切割顺序,依次从左往右摆放,产品的摆放方式有两种,竖着摆放还是横着摆放,第一层肯定不用考虑板材的宽度,肯定是够的,那么从第二次从左往右摆放时,就要注意板材的剩余宽度,如果不够,那么顺延,依次类推,这样就算你是用蒙克卡洛随机模拟,都能很轻松解决这道题,之前我用蚁群算法做了一很相似的案例,案例下载:https://wwp.lanzouv.com/iDT4R0dbemxe,案例程序的角度出于在一个足够面积的板材上,进行裁剪,利用率根据下面红色线以下的部分来计算的,这样会得到一个尽可能紧密的排布方式

注意组委会有通知:取消数据dataA5
B题我还在做,需要可以私聊。
C题思路
思路仅供参考,暂时没有时间去实践:
题目的目标函数和约束条件都写得很清楚,就不用多说,目标函数4个,多目标寻优,多目标排序用ns2,最终要得到的就是车辆的最优排序,关于题目说的输出结果,按照排序推算下就可以了。
本题的启发式算法很简单,大家也可以按我说的方式从简设计,想套什么优化算法都可以。针对种群中每个个体随机产生一组车辆排序,然后再对每个排序中的车辆产生一组1-6条流水线的编号,约束条件再增加一个,必须所有流水线上要有加工的车辆,这就是做法,用蒙塔卡洛随机模拟就行,这里我也上传一个类似的案例吧,C题参考程序框架直接下载:https://wwp.lanzouv.com/iDuEe0dbtb5a
C题题目说到的一些约束条件和目标函数一定要仔细检查。
D题思路
思路仅供参考,暂时没有时间去实践:
题目所指的级数,可以理解为支点个数,根据表3可以得到各个基本块之间的连接关系,第一问的级数最短寻优,这道题主要是基本块的选择问题,0级为编号0的基本块,通过启发式算法寻优在保证所有变量按写读顺序处理后的最短级数,类似于树状结构,并且同一层级资源有所限制,如果级数超过15,那么还有对折级限制
For 循环产生个体
while 所有变量可以按写读顺序处理
对每个连接关系赋予0-1变量,1表示连接,0表示取消连接,这样会得到以0为开始点的一个树状结构,并且这个树状结构要同时满足资源约束以及所有变量都需要被写读,则终止while循环,输出流程方案
每个个体为一种流程方案,目标函数为所有级数
第二问,一个基本块同时连接了两个基本块,即使这两个基本块有连接,那么在这种树状结构中,不能相连,其实就是在第一问程序上,加一个连接的判断,如果出现图3的情况,直接把变量改为0,除了约束条件,其他步骤无变化
E题思路
做完了已经,简单透露下:
问题一就是微分方程;
问题二就是预测,那么就是用机器学习中的监督学习算法进行预测就好了;
问题三:预测,还可以继续机器学习算法,可以跟问题二不一样做一些升级哈
问题四:我用的遗传算法
问题五:多目标规划
问题六就是时间序列嘛,选一个时间序列模型哈,不熟悉哪个更适合的,可以全部试一遍,谁更好选谁。。。。
E题卖五份,感兴趣私聊。
F题思路
思路仅供参考,暂时没有时间去实践。
问题一:
一般疫情传播分为两个阶段:
- 自由传播阶段,可以用SIR传播理论进行建模。
- 政府介入之后,进行强制隔离、或者自行居家隔离,使得疾病传播再生数小于1呈现出下降趋势,这就是拐点。
故需要根据两阶段分别进行建模。
在上面的基础上还可以使用机器学习算法进行建模,使用多种对比拟合效果进行选择建模、预测,谁效果好就用谁。
问题二:建立数学中的目标规划模型很重要。
目标函数:
最小化(全部的选址半径和)
约束条件:
每个小区都被一个生活物资投放点包含
生活物资投放点之间的半径不重合
最小/最大半径(从而不出现不合理的点,人力资源有限,不可能无限制扩张)
问题三:可以参考数据包络分析分析(DEA)
声明一下
部分思路参考了网络,觉得不错。一天时间我肯定是没法全部看完,第一天只做完了E题,B题快做一半了,这是我目前的进度。
感兴趣可以点击下方卡片加我微信。